问:电流源的输出阻抗测试方法
请问各位高手:一个电流源,如何测试出它的输出阻抗?最近一个LCR电桥外加一个直流源来测试电感元件的直流叠加特性,可是这两个仪器的阻抗不配,LCR为50欧,直流源为30欧,如何修改成它们配合状态?
全部回复(9)
正序查看
倒序查看
现在还没有回复呢,说说你的想法
1.先讲下电压源:设电压源开路电压为U,内阻为r,接上阻值为R1的负载时端电压为U1,流过R1的电流为I1则有I1=U/(R1+r),U1=I1R1;同理接上阻值为R2的负载时端电压为U2,流过R2的电流为I2则有I2=U/(R2+r),U2=I2R2,通过计算可得出:r=(U2-U1)/(I1-I2).从这个公式可以看出,电压源的内阻它反应了一种对不同的输出电流端电压的保持能力,理想的电压源内阻为零而且不能短路,U=U1=U2.
2.关于电流源:设电流源短路电流为I,内阻为r,接上阻值为R1的负载时端电压为U1,流过R1的电流为I1,流过内阻的电流为Ir1则有I=Ir1+I1,U1=r*Ir1=R1*I1同理接上阻值为R2的负载时端电压为U2,流过R2的电流为I2,流过内阻的电流为Ir2则有I=Ir2+I2,U2=r*Ir2=R2*I2通过计算可得出r=(U2-U1)/(I1-I2).可以看出这个公式和电压源的内阻公式一样,不过它反应的是一种对不同的输出电压端电流的保持能力,理想的电流源内阻为无限大,而且不能开路I=I1=I2.
3.区别与联系:电压源的内阻和负载是串联的,越小越好,电压源的内阻和负载是并联的,越大越好;理想的电压源不能短路否则输出电流会无限大,理想的电流源不能开路路否则输出电压会无限大.
4.理解了它们的基本原理,至于怎样测量它们的内阻我想我就不用讲了.
2.关于电流源:设电流源短路电流为I,内阻为r,接上阻值为R1的负载时端电压为U1,流过R1的电流为I1,流过内阻的电流为Ir1则有I=Ir1+I1,U1=r*Ir1=R1*I1同理接上阻值为R2的负载时端电压为U2,流过R2的电流为I2,流过内阻的电流为Ir2则有I=Ir2+I2,U2=r*Ir2=R2*I2通过计算可得出r=(U2-U1)/(I1-I2).可以看出这个公式和电压源的内阻公式一样,不过它反应的是一种对不同的输出电压端电流的保持能力,理想的电流源内阻为无限大,而且不能开路I=I1=I2.
3.区别与联系:电压源的内阻和负载是串联的,越小越好,电压源的内阻和负载是并联的,越大越好;理想的电压源不能短路否则输出电流会无限大,理想的电流源不能开路路否则输出电压会无限大.
4.理解了它们的基本原理,至于怎样测量它们的内阻我想我就不用讲了.
0
回复
提示
@xzszrs
1.先讲下电压源:设电压源开路电压为U,内阻为r,接上阻值为R1的负载时端电压为U1,流过R1的电流为I1则有I1=U/(R1+r),U1=I1R1;同理接上阻值为R2的负载时端电压为U2,流过R2的电流为I2则有I2=U/(R2+r),U2=I2R2,通过计算可得出:r=(U2-U1)/(I1-I2).从这个公式可以看出,电压源的内阻它反应了一种对不同的输出电流端电压的保持能力,理想的电压源内阻为零而且不能短路,U=U1=U2.2.关于电流源:设电流源短路电流为I,内阻为r,接上阻值为R1的负载时端电压为U1,流过R1的电流为I1,流过内阻的电流为Ir1则有I=Ir1+I1,U1=r*Ir1=R1*I1同理接上阻值为R2的负载时端电压为U2,流过R2的电流为I2,流过内阻的电流为Ir2则有I=Ir2+I2,U2=r*Ir2=R2*I2通过计算可得出r=(U2-U1)/(I1-I2).可以看出这个公式和电压源的内阻公式一样,不过它反应的是一种对不同的输出电压端电流的保持能力,理想的电流源内阻为无限大,而且不能开路I=I1=I2.3.区别与联系:电压源的内阻和负载是串联的,越小越好,电压源的内阻和负载是并联的,越大越好;理想的电压源不能短路否则输出电流会无限大,理想的电流源不能开路路否则输出电压会无限大.4.理解了它们的基本原理,至于怎样测量它们的内阻我想我就不用讲了.
带载等效原理图: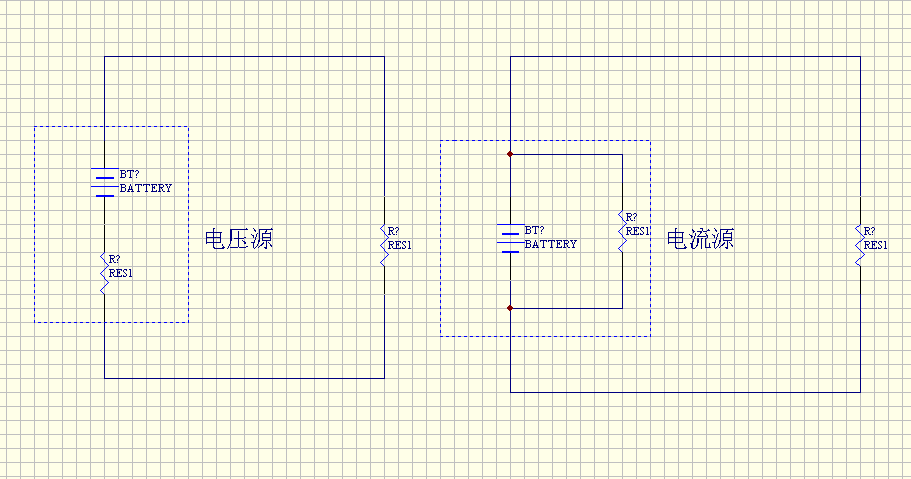 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/60/700751198721319.gif');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/60/700751198721319.gif');}" onmousewheel="return imgzoom(this);">
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/60/700751198721319.gif');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/60/700751198721319.gif');}" onmousewheel="return imgzoom(this);"> 0
回复
提示
@xzszrs
带载等效原理图:[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/60/700751198721319.gif');}"onmousewheel="returnimgzoom(this);">
老兄搂主现在的问题不是如何测量内阻啊
0
回复
提示
@xzszrs
我相信楼主看了我的贴子,他的问题他就知道就解决了.
众所周知,铁氧体磁芯在各种电子电路,例如转换电路以及开关调节电路中得到了非常广泛的应用.在很多电路中的器件通常是在有直流的状态下工作.最典型的例子就是行输出变压器、平滑扼流圈以及枕校变压器等.在有直流的状态下工作的铁氧体磁芯除了必须保持良好的电磁特性外,还必须具有很好的直流叠加特性.
为适应电子技术的需要,现代功率铁氧体材料已经得到很大的发展.一般说来,功率铁氧体材料主要分为两大类:一类用于高频开关电源,另一类用于高清晰度彩电和显示器.主要用于高频开关电源的功率铁氧体材料有两大发展趋势,一是向超低功耗方向发展,目前这些材料已经系列化,典型代表如日本TDK公司的PC40、PC44、PC45、PC46、PC47.其中,PC45和PC46这两种材料主要是针对特殊电路的需要而开发的超低功耗MnZn铁氧体材料(功耗最低点温度有所差异);而PC40、PC44、PC47功耗差别很大,在f=100kHz,Bm=200mT,T=100℃条件下,三者功耗分别为410mW/cm3、300mW/cm3和200mW/cm3.二是向高频化方向发展,如日本TDK公司PC50材料可用至1MHz,荷兰Philips公司的3F4材料可用至3MHz(这种材料适用于谐振式电源变压器).当f>3MHz时,则通常采用NiZn材料,如Philips公司的4F1材料,可使用至10MHz.作者以前曾对世界各著名铁氧体公司的超低功耗以及高频低功耗功率铁氧体材料作过详细介绍[1],在此不再重复.
高清晰度彩电以及高分辨率显示器用功率铁氧体材料的优点是:(1)饱和磁通密度高(Bs≥500mT);(2)宽频低功耗,对于这类材料目前使用频率一般不超过100kHz,但要求16kHz~100kHz范围内功耗都比较低;(3)直流叠加特性优良,这是这类材料最突出的优点,以日本TDK公司的HV22、HV38、HV40、HV45为典型代表,但在日本TDK公司1999年产品目录上只保留两种材料即HV22和HV45[2].目前,国内已有少数几个工厂能够批量生产相当于TDK HV22、HV38的产品,而对于HV40、HV45的产品,国内还没有哪个厂家能够稳定生产.因此,必须尽快研制开发,这是国内软磁行业所面临的迫切任务.
2 直流叠加特性描述
描述软磁材料动态特性的参量很多,如复数磁导率、品质因数、损耗特性、减落等[3].对于工作在直流偏磁化场的状态而言,直流叠加特性也是软磁材料的重要性能参数,也是软磁材料的动态特性之一.交直流磁场的叠加一般分为两种方式,一种是交流场与直流偏磁化场垂直,另一种是交流场与偏磁化场平行.实际上,使用较多的是平行叠加方式.
软磁铁氧体材料的性能往往会由于叠加直流磁化场而发生显著的变化,最明显的就是磁导率的变化.在有偏磁场存在的情况下,材料的磁导率称为“可逆磁导率μrev”,V.W.kampcgyk等人对MnZn铁氧体的研究结果表明,可逆磁导率并非单纯只与磁场强度有关,而且还与其磁化历史有关.当直流磁场H-沿磁滞回线变化时,可逆磁导率呈典型的蝶形曲线[4],如图1所示.
实践证明,磁导率随直流偏磁化场的增大而降低,下降的陡峭程度取决于磁滞回线的形状,也就是说完全取决于材料的成分、制造工艺以及磁芯之间的气隙大小.通常在开关调节电路中,希望由于出现不可避免的直流偏磁化场而使磁导率下降的幅度变小;而在磁控可变电感器中,则希望改变直流偏磁场时,能使磁导率灵敏地变化.
S.Wada等[5]曾经研究了直流叠加对电工铁(硅钢片)功耗、磁致伸缩及噪音的影响.指出,当磁通密度较低时,功耗将随着直流磁场的增大而增大;而当磁通密度较高时,功耗几乎不随直流磁场而变.其解释是:在低磁通密度条件下,硅钢片涡流损耗可近似表达为
Pe=1/2π3/2f3/2B2σ1/2μ-1/2a
式中,σ为电导率;μ为磁导率;a为硅钢片厚度;f为频率;B为磁通密度.由于铁芯的磁导率将随着直流场的增大而下降,由上式不难看出,Pe将上升.但在较高的磁通密度条件下,铁芯内部的磁通密度的变化将与薄片表面的相同,此时涡流损耗将与磁导率无关.
另一个值得注意的现象是:由于直流叠加,电工铁在交流磁场下的磁致伸缩出现不对称,从而使噪声变大.图2显示了不同直流偏磁场条件下,铁芯的噪音随电压的变化.图3则是磁致伸缩蝶形曲线随直流偏磁场的变化.
M.Murasato等提出用在直流偏磁场磁化场状态下工作的磁芯温升来评价铁氧体磁芯的性能,这样更接近于磁芯的真实工作状态.图4a为通常情况下,测量磁芯功耗时的电压、电流波形;图4b为叠加直流后的锯齿波形,这是磁芯的实际使用状态[6].
Murasato的研究结果是:随着直流偏磁场的增强,磁芯的温升几乎呈线性上升,如图5.对于在通常情况下测量的功耗最低的磁芯,在叠加直流后,其温升却不是最低,如图6.
3 直流叠加特性测量原理
为简化测量装置,在测试磁芯电感直流叠加特性时,可采用图7a所示的测量原理.这一原理比较简单,但严格说来,测量线圈产生的交变磁场将会在偏磁化线圈中感应出交变电压,而一般情况下,偏磁化线圈匝数要大大高于测量线圈,因此,感应出的交变电压还是挺高的,好在直流磁化源内阻可以看成是非常大,感应电流可以忽略不计.
严格的测量,特别是直流偏磁场下功耗的测量应采用图7b所示的测量原理.磁芯1和磁芯2由同种材料制成且尺寸相同,这两个磁芯上的偏磁化线圈绕制方向相反,即串联反接,这样在这两线圈中的感生电动势方向相反而自动抵消.在该测量方法中,功耗仪显示功耗为两磁芯功耗之和.
如果仅仅需要了解磁芯电感的直流叠加特性,可以采用图7c所示的更简化的测量原理图.
在测量不同直流偏磁场下的磁芯可逆磁导率以及功耗时,为防止直流线圈长时间通电过热,每测完一点必须切断电源,同时为消除磁滞(图1)引起的μrev差异,必须通过测量线圈加入交变磁场,并逐渐减小到0(消磁).本研究中,测试磁环电感直流叠加特性时,采用图7a原理,电感测量仪采用HP4274A LCR表,而直流偏磁条件下功耗特性的测量则采用图7b原理(环状磁芯直流磁化线圈50匝,交流测量线圈20匝).
4 MnZn铁氧体材料及磁芯直流叠加特性
4.1 磁芯电感直流叠加特性
关于带有气隙的铁氧体磁芯(如U形磁芯)的电感直流叠加特性,作者以前已作过研究[7].指出,要改善磁芯的直流叠加特性,主要可通过以下两个途径:一是通过调节磁芯的空气隙厚度来实现,当然,这必须借助于Hanna曲线来确定磁芯的最佳气隙和绕组匝数.二是通过改变材料配方或是调整烧结工艺来实现.但是烧结工艺的改变必须以不恶化磁芯其它电磁性能为原则.作者认为第二种方法应当更为有效,这是由于加大空气隙厚度,往往导致磁芯漏磁增大,无疑是不利的.
4.2 直流叠加条件下,材料的电感及品质因数的频率特性
图8为在直流磁化场102A/m,环境温度t=8℃条件下,环状磁芯电感L、品质因数Q值随测试频率的变化(测量线圈20匝,直流磁化线圈50匝,测试电流0.2mA).不难看出,在300Hz~40kHz范围内,电感呈上升趋势;而Q值在f=10kHz时达最大值,当f<300Hz或f>50kHz时,Q值趋于0.值得注意的是,叠加直流对Q值曲线的形状、峰值大小及其位置有显著的影响,未叠加直流时,磁芯Q值峰值位置在f=50kHz,其大小为180,在f=10kHz和100kHz时,Q值分别为90和140.
必须指出的是,在直流偏磁化场为102A/m时,当f≥100kHz,L变为负值,而当f=100Hz或50kHz时,L值出现如图9所示的振荡现象.我们知道材料的磁化率主要来自于两方面的贡献,即转动磁化率和畴壁位移磁化率,材料的电感L出现振荡,说明以上某一方面或两方面都存在某种振荡效应.根据铁磁学理论[8],软磁材料的磁化曲线分为初始磁化、不可逆磁化、可逆转动、趋近饱和等四个阶段.因此,直流偏磁场的大小以及磁芯的技术磁化过程对电感的振荡效应可能有直接的影响.
4.3 直流叠加条件下材料的功耗特性
对于环状磁芯在直流叠加条件下的功耗特性,作者以前已作过研究[9].与传统的材料相比,新开发的材料,在直流偏场H=10A/m处获得最低功耗,此后随直流偏场的增加而线性增加.众所周知,在f<300kHz时,MnZn铁氧体磁芯损耗主要来自两个方面,一是磁滞损耗,二是涡流损耗.磁芯在H=10A/m处获得最低的功耗,说明此时磁滞损耗变小(即磁滞回线面积变小);或者是涡流损耗变小,这可能要借助于微磁学理论才能解释;或者两者兼而有之.
值得指出的是,我们所采用的磁环在没有直流叠加时(偏磁化线路断路),其功耗很低[9].但采用图7b所示的原理测量后,尽管调节直流磁化源电流输出为0,但磁芯功耗明显增大.这可能是两磁环的直流磁化线圈中感应的交流电压未完全抵消,从而在与直流磁化源构成的回路中产生感生电流,消耗部分功率;或者是直流源显示灵敏度不够造成的,有关这方面还需作深入研究.
4.4 直流叠加条件下磁芯的噪音
在测试过程中我们发现,当采用图7a所示测量原理,将直流源输出调至0.5A(即磁化场为320A/m)时,若将测量端的电压调至6.5V(f=16kHz),则直流源电流显示消失,磁芯发出尖锐的噪声,功耗显示达500mW/g,仅几秒钟,磁芯即发热;而如果直流线路断路,在测量端加入电压6.5V(16kHz)则听不到噪声.
磁芯噪声一般认为是由磁致伸缩引起的.叠加直流后,由于直流偏磁场在一个信号周期内,磁芯内部正向磁场强度与反向磁场强度相差2倍的偏磁场,从而使磁致伸缩出现严重的不对称,并且这种不对称将随着偏磁场的增大而愈为严重.
当我们采用图7b所示的测量原理时,直流偏磁场只能加到64A/m,若再增加则功耗仪阻抗无法匹配,没有电压输出,由于直流偏磁场较小,没有听到噪声.
5 结论
(1)直流叠加条件下,电感对频率存在明显的依赖性,在一定范围内随频率的升高而增大,品质因数Q值峰值大幅度下降,峰值位置向低频方向移动.
(2)直流叠加条件下,在较低频率(f=300Hz)和较高频率(f=50kHz)时,电感随时间的变化呈明显的振荡效应,有待深入研究.
(3)不同材料的功耗随着偏磁场的变化情况呈现不同的特性,新开发的材料除了整体功耗大幅度下降外,还具有功耗最低点,这对使用无疑是十分有利的.
(4)较大的偏磁场容易使材料的磁致伸缩出现严重的不对称,从而产生噪声.
为适应电子技术的需要,现代功率铁氧体材料已经得到很大的发展.一般说来,功率铁氧体材料主要分为两大类:一类用于高频开关电源,另一类用于高清晰度彩电和显示器.主要用于高频开关电源的功率铁氧体材料有两大发展趋势,一是向超低功耗方向发展,目前这些材料已经系列化,典型代表如日本TDK公司的PC40、PC44、PC45、PC46、PC47.其中,PC45和PC46这两种材料主要是针对特殊电路的需要而开发的超低功耗MnZn铁氧体材料(功耗最低点温度有所差异);而PC40、PC44、PC47功耗差别很大,在f=100kHz,Bm=200mT,T=100℃条件下,三者功耗分别为410mW/cm3、300mW/cm3和200mW/cm3.二是向高频化方向发展,如日本TDK公司PC50材料可用至1MHz,荷兰Philips公司的3F4材料可用至3MHz(这种材料适用于谐振式电源变压器).当f>3MHz时,则通常采用NiZn材料,如Philips公司的4F1材料,可使用至10MHz.作者以前曾对世界各著名铁氧体公司的超低功耗以及高频低功耗功率铁氧体材料作过详细介绍[1],在此不再重复.
高清晰度彩电以及高分辨率显示器用功率铁氧体材料的优点是:(1)饱和磁通密度高(Bs≥500mT);(2)宽频低功耗,对于这类材料目前使用频率一般不超过100kHz,但要求16kHz~100kHz范围内功耗都比较低;(3)直流叠加特性优良,这是这类材料最突出的优点,以日本TDK公司的HV22、HV38、HV40、HV45为典型代表,但在日本TDK公司1999年产品目录上只保留两种材料即HV22和HV45[2].目前,国内已有少数几个工厂能够批量生产相当于TDK HV22、HV38的产品,而对于HV40、HV45的产品,国内还没有哪个厂家能够稳定生产.因此,必须尽快研制开发,这是国内软磁行业所面临的迫切任务.
2 直流叠加特性描述
描述软磁材料动态特性的参量很多,如复数磁导率、品质因数、损耗特性、减落等[3].对于工作在直流偏磁化场的状态而言,直流叠加特性也是软磁材料的重要性能参数,也是软磁材料的动态特性之一.交直流磁场的叠加一般分为两种方式,一种是交流场与直流偏磁化场垂直,另一种是交流场与偏磁化场平行.实际上,使用较多的是平行叠加方式.
软磁铁氧体材料的性能往往会由于叠加直流磁化场而发生显著的变化,最明显的就是磁导率的变化.在有偏磁场存在的情况下,材料的磁导率称为“可逆磁导率μrev”,V.W.kampcgyk等人对MnZn铁氧体的研究结果表明,可逆磁导率并非单纯只与磁场强度有关,而且还与其磁化历史有关.当直流磁场H-沿磁滞回线变化时,可逆磁导率呈典型的蝶形曲线[4],如图1所示.
实践证明,磁导率随直流偏磁化场的增大而降低,下降的陡峭程度取决于磁滞回线的形状,也就是说完全取决于材料的成分、制造工艺以及磁芯之间的气隙大小.通常在开关调节电路中,希望由于出现不可避免的直流偏磁化场而使磁导率下降的幅度变小;而在磁控可变电感器中,则希望改变直流偏磁场时,能使磁导率灵敏地变化.
S.Wada等[5]曾经研究了直流叠加对电工铁(硅钢片)功耗、磁致伸缩及噪音的影响.指出,当磁通密度较低时,功耗将随着直流磁场的增大而增大;而当磁通密度较高时,功耗几乎不随直流磁场而变.其解释是:在低磁通密度条件下,硅钢片涡流损耗可近似表达为
Pe=1/2π3/2f3/2B2σ1/2μ-1/2a
式中,σ为电导率;μ为磁导率;a为硅钢片厚度;f为频率;B为磁通密度.由于铁芯的磁导率将随着直流场的增大而下降,由上式不难看出,Pe将上升.但在较高的磁通密度条件下,铁芯内部的磁通密度的变化将与薄片表面的相同,此时涡流损耗将与磁导率无关.
另一个值得注意的现象是:由于直流叠加,电工铁在交流磁场下的磁致伸缩出现不对称,从而使噪声变大.图2显示了不同直流偏磁场条件下,铁芯的噪音随电压的变化.图3则是磁致伸缩蝶形曲线随直流偏磁场的变化.
M.Murasato等提出用在直流偏磁场磁化场状态下工作的磁芯温升来评价铁氧体磁芯的性能,这样更接近于磁芯的真实工作状态.图4a为通常情况下,测量磁芯功耗时的电压、电流波形;图4b为叠加直流后的锯齿波形,这是磁芯的实际使用状态[6].
Murasato的研究结果是:随着直流偏磁场的增强,磁芯的温升几乎呈线性上升,如图5.对于在通常情况下测量的功耗最低的磁芯,在叠加直流后,其温升却不是最低,如图6.
3 直流叠加特性测量原理
为简化测量装置,在测试磁芯电感直流叠加特性时,可采用图7a所示的测量原理.这一原理比较简单,但严格说来,测量线圈产生的交变磁场将会在偏磁化线圈中感应出交变电压,而一般情况下,偏磁化线圈匝数要大大高于测量线圈,因此,感应出的交变电压还是挺高的,好在直流磁化源内阻可以看成是非常大,感应电流可以忽略不计.
严格的测量,特别是直流偏磁场下功耗的测量应采用图7b所示的测量原理.磁芯1和磁芯2由同种材料制成且尺寸相同,这两个磁芯上的偏磁化线圈绕制方向相反,即串联反接,这样在这两线圈中的感生电动势方向相反而自动抵消.在该测量方法中,功耗仪显示功耗为两磁芯功耗之和.
如果仅仅需要了解磁芯电感的直流叠加特性,可以采用图7c所示的更简化的测量原理图.
在测量不同直流偏磁场下的磁芯可逆磁导率以及功耗时,为防止直流线圈长时间通电过热,每测完一点必须切断电源,同时为消除磁滞(图1)引起的μrev差异,必须通过测量线圈加入交变磁场,并逐渐减小到0(消磁).本研究中,测试磁环电感直流叠加特性时,采用图7a原理,电感测量仪采用HP4274A LCR表,而直流偏磁条件下功耗特性的测量则采用图7b原理(环状磁芯直流磁化线圈50匝,交流测量线圈20匝).
4 MnZn铁氧体材料及磁芯直流叠加特性
4.1 磁芯电感直流叠加特性
关于带有气隙的铁氧体磁芯(如U形磁芯)的电感直流叠加特性,作者以前已作过研究[7].指出,要改善磁芯的直流叠加特性,主要可通过以下两个途径:一是通过调节磁芯的空气隙厚度来实现,当然,这必须借助于Hanna曲线来确定磁芯的最佳气隙和绕组匝数.二是通过改变材料配方或是调整烧结工艺来实现.但是烧结工艺的改变必须以不恶化磁芯其它电磁性能为原则.作者认为第二种方法应当更为有效,这是由于加大空气隙厚度,往往导致磁芯漏磁增大,无疑是不利的.
4.2 直流叠加条件下,材料的电感及品质因数的频率特性
图8为在直流磁化场102A/m,环境温度t=8℃条件下,环状磁芯电感L、品质因数Q值随测试频率的变化(测量线圈20匝,直流磁化线圈50匝,测试电流0.2mA).不难看出,在300Hz~40kHz范围内,电感呈上升趋势;而Q值在f=10kHz时达最大值,当f<300Hz或f>50kHz时,Q值趋于0.值得注意的是,叠加直流对Q值曲线的形状、峰值大小及其位置有显著的影响,未叠加直流时,磁芯Q值峰值位置在f=50kHz,其大小为180,在f=10kHz和100kHz时,Q值分别为90和140.
必须指出的是,在直流偏磁化场为102A/m时,当f≥100kHz,L变为负值,而当f=100Hz或50kHz时,L值出现如图9所示的振荡现象.我们知道材料的磁化率主要来自于两方面的贡献,即转动磁化率和畴壁位移磁化率,材料的电感L出现振荡,说明以上某一方面或两方面都存在某种振荡效应.根据铁磁学理论[8],软磁材料的磁化曲线分为初始磁化、不可逆磁化、可逆转动、趋近饱和等四个阶段.因此,直流偏磁场的大小以及磁芯的技术磁化过程对电感的振荡效应可能有直接的影响.
4.3 直流叠加条件下材料的功耗特性
对于环状磁芯在直流叠加条件下的功耗特性,作者以前已作过研究[9].与传统的材料相比,新开发的材料,在直流偏场H=10A/m处获得最低功耗,此后随直流偏场的增加而线性增加.众所周知,在f<300kHz时,MnZn铁氧体磁芯损耗主要来自两个方面,一是磁滞损耗,二是涡流损耗.磁芯在H=10A/m处获得最低的功耗,说明此时磁滞损耗变小(即磁滞回线面积变小);或者是涡流损耗变小,这可能要借助于微磁学理论才能解释;或者两者兼而有之.
值得指出的是,我们所采用的磁环在没有直流叠加时(偏磁化线路断路),其功耗很低[9].但采用图7b所示的原理测量后,尽管调节直流磁化源电流输出为0,但磁芯功耗明显增大.这可能是两磁环的直流磁化线圈中感应的交流电压未完全抵消,从而在与直流磁化源构成的回路中产生感生电流,消耗部分功率;或者是直流源显示灵敏度不够造成的,有关这方面还需作深入研究.
4.4 直流叠加条件下磁芯的噪音
在测试过程中我们发现,当采用图7a所示测量原理,将直流源输出调至0.5A(即磁化场为320A/m)时,若将测量端的电压调至6.5V(f=16kHz),则直流源电流显示消失,磁芯发出尖锐的噪声,功耗显示达500mW/g,仅几秒钟,磁芯即发热;而如果直流线路断路,在测量端加入电压6.5V(16kHz)则听不到噪声.
磁芯噪声一般认为是由磁致伸缩引起的.叠加直流后,由于直流偏磁场在一个信号周期内,磁芯内部正向磁场强度与反向磁场强度相差2倍的偏磁场,从而使磁致伸缩出现严重的不对称,并且这种不对称将随着偏磁场的增大而愈为严重.
当我们采用图7b所示的测量原理时,直流偏磁场只能加到64A/m,若再增加则功耗仪阻抗无法匹配,没有电压输出,由于直流偏磁场较小,没有听到噪声.
5 结论
(1)直流叠加条件下,电感对频率存在明显的依赖性,在一定范围内随频率的升高而增大,品质因数Q值峰值大幅度下降,峰值位置向低频方向移动.
(2)直流叠加条件下,在较低频率(f=300Hz)和较高频率(f=50kHz)时,电感随时间的变化呈明显的振荡效应,有待深入研究.
(3)不同材料的功耗随着偏磁场的变化情况呈现不同的特性,新开发的材料除了整体功耗大幅度下降外,还具有功耗最低点,这对使用无疑是十分有利的.
(4)较大的偏磁场容易使材料的磁致伸缩出现严重的不对称,从而产生噪声.
0
回复
提示

