在设计LLC电路时多数会采用基波分析法(FHA),按这种方法绘制的DC特性曲线如下:

图1-1 基于FHA的DC特性曲线
而实际电路中当开关频率偏离谐振频率时这种基波分析法会产生偏差,见下图的Ti理论与实测对比。

图1-2 FHA曲线与实测点对比
这里准备采用求解时域方程的方法来获取较准确的DC特性曲线,并试图为FHA方法找出一个修正函数以简化时域方程计算。
在设计LLC电路时多数会采用基波分析法(FHA),按这种方法绘制的DC特性曲线如下:

图1-1 基于FHA的DC特性曲线
而实际电路中当开关频率偏离谐振频率时这种基波分析法会产生偏差,见下图的Ti理论与实测对比。

图1-2 FHA曲线与实测点对比
这里准备采用求解时域方程的方法来获取较准确的DC特性曲线,并试图为FHA方法找出一个修正函数以简化时域方程计算。
上述方程中正弦波的峰值A0是未知的,可以通过输出功率或输出电流反推出来,输出二极管电流波形为漏感电流和励磁电流之差,如下:
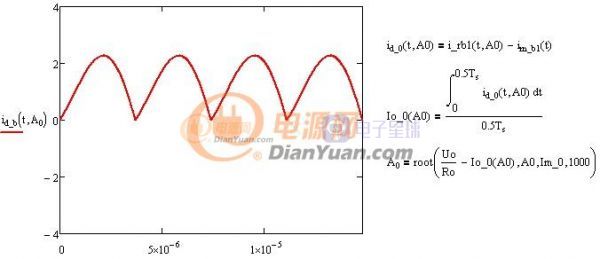
图1-5 输出二极管电流波形
利用积分公式求出上述电流波形的平均值既为输出电流Io=Uo/Ro,实际计算过程是反推由输出电流Io求正弦峰值电流A0。
在推导过程遇到了不少问题(主要是运算速度的问题),还有最后一个方程有待验证,推导过程如下:
步奏1
先设置一个起点电流Im0_u和谐振电流幅值A0_u,可以绘制出在时间0.5Tr附近前的波形(两条曲线的交点不等于0.5Tr),见下图。
图2-3-1 时间0~0.512Tr段漏感电流与励磁电流波形
利用root工具可以求解出两条曲线的相交时间及相交电流。在前面提到为了提高运算速度特将积分运算都转换成三角函数运算,这里当root工具调用次数过多时也会影响运算速度,因而如果能将方程整理出来效果会更好。
步奏2
对阴影区域积分获取输出电流函数并增加输出电流等于Uo/Ro这一约束条件。
图2-3-2等输出电流曲线
从上图看满足输出电流恒定的曲线有很多,因而还需其它约束条件(方程)。
非积分形式的输出电流推导如下:
图2-3-3 输出电流原始推导公式
问题2:需要先处理好问题1的方程整理,推导出方程A0=f(Im0,Io)。
上述步奏4中曲线相切的方法作为约束条件行不通,经验证在t1时刻无论Im0取何值两条曲线都是相切的,目前仍缺少一个约束条件。
参考仿真波形中的Im0进行设置并获得如下对比曲线:
图2-3-6 等Q值不同开关频率下的波形对比
通过波形对比可知计算公式是准确的,如果能确定Im0电流那么输出/输入的DC增益也就可以确定了。
步奏5
根据输入、输出能量守恒来确认参数Im0,由于匝比设置为1:1所以输入电流和谐振腔电流波形一样,见下图:
图2-3-7 输入电流
有一点区别就输入电流只占1/2周期,因而在计算时输入电压都是按1/2Vin来的。
根据能量守恒Uo*Io=0.5*Uin*Iin(Iin≠Io差个Im)推出Uin=2*Uo*Io/Iin,再参照下图的谐振电容波形,
图2-3-8 谐振电容“升压”值
参照上图输入电压Uin=2*Uo-△U,当满足两个Uin相等时可解出参数Im0。
对方程进行验证:
图2-4-1 fs=100kHz,Ro=142.86,Gdc=1.201
输出200V,负载Ro=142.86,谐振频率fr=135kHz,开关频率fs=100kHz,计算出输入电压333V,直流增益1.2。
图2-4-2 fs=80kHz,Ro=142.86,Gdc=1.583
输出200V,负载Ro=142.86,谐振频率fr=135kHz,开关频率fs=80kHz,计算出输入电压253V,直流增益1.583。
上面的参数是根据Ti资料中的参数设置的,再对比一下Ti的实测值:
图2-4-3 Ti实测增益值
在100kHz和80kHz处计算值同实测值几乎一样,在其它条件下用Saber仿真软件进行验证得出的结果也基本是准确的。
这里的方程大多是多解,而root函数只能得出单一的解(Mathcad中是否有可以求多解的功能?),如果将root函数中的定义域进行细分倒是可以解出多解来。
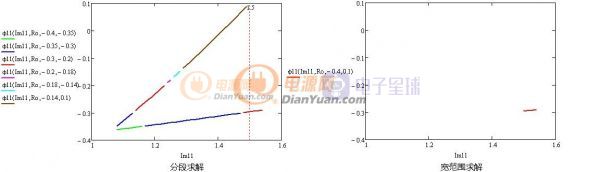
图2-5 利用分段定义域求方程多解
如上图,定义域细分的可以解出所有的解,宽定义域的只能得出最后一小段曲线(多解的情况下),这里可以编写一个程序来自动细分定义域。
输出平均电流的计算经整理得到如下方程:
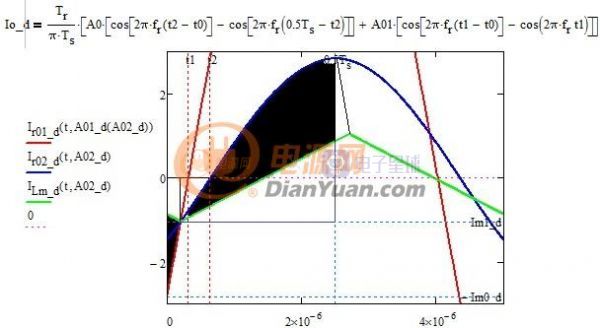
图3-4 输出平均电流方程
根据Io_d=Vor/Ro可以得出谐振电流峰值表达式,再列出谐振电容电压方程如下:
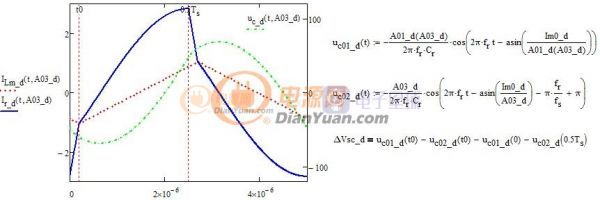
图3-5 谐振电容电压公式及波形
最后根据输入、输出能量守恒解出整个方程组。

