分享LLC_DC增益设计（离散微积分）-电源网 https://www.dianyuan.com/bbs/2472194.html
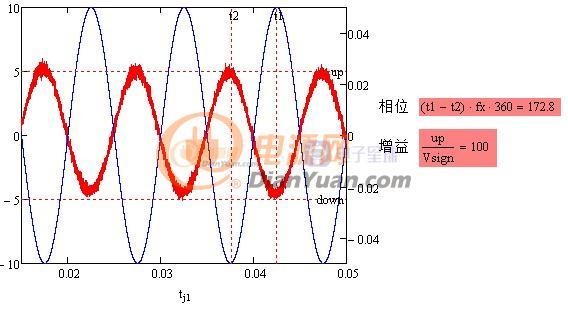
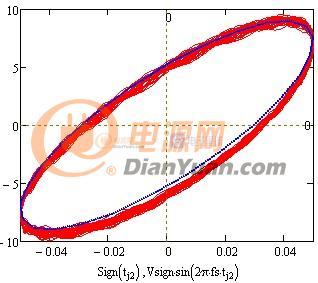
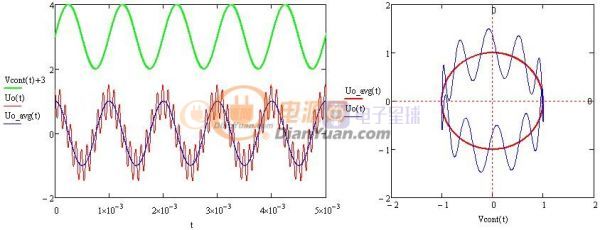
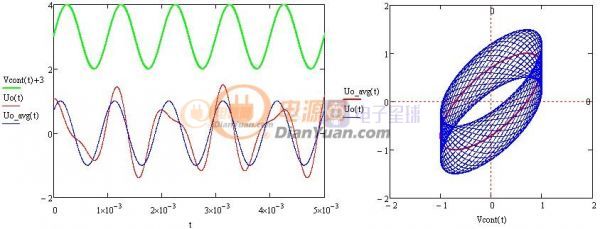
接上贴再来一下基于离散微积分的LLC小信号分析。其方法同仿真软件相似，可为电路设计多一种思路。初版还不太成熟只支持单点分析而后连点成线，相位和增益的判断依靠目测。
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
LLC_smallsign_saber07 （Saber07仿真文件）
LLC_smallsign_mathcad （Mathcad文件）
基本原理是先模拟一个VCO（压控振荡器）作为LLC电路的驱动，选择一个直流工作点在其上注入交流小信号，通过测量输出电压波形对比增益和相位的变化，接着改变注入信号的频率逐次绘制出整个频域的bode图。
使用方法：
1、时域目测法
图1-1 时域波形目测法
上图蓝色曲线为输入扰动信号，红色曲线为输出电压交流量（有做带通滤波处理），二者的相位差为（t1-t2）*fx*360，其中fx为扰动信号的频率，输出/输入增益为二者峰值电压之比。
2、利萨茹曲线目测法
图2-1 利萨茹曲线目测法
通过调整图中蓝色曲线的增益和相位使其与红色曲线重合，当前的增益和相位既为所要求解的值。
当注入的扰动信号频率接近于或者高于开关、谐振频率时，滤波器很难设计采用时域法较难分辨出来。
图2-2 高频噪声时域波与利萨茹曲线
图2-3 低频噪声下时域波与利萨茹曲线
图2-2绿线为输入端注入的扰动，红线为输出交流量，蓝线为我们所需的去掉开关及谐振噪声的输出量。采用低通滤波器也可以将蓝色信号滤出来，不过当红线和蓝线频率接近时滤波效果并不好还会带来幅值和相位的偏移引入测量误差。利萨茹曲线法不需要经过滤波没有上述问题，不过利萨茹曲线需要多个周期的数据才能成成如上图2-3的效果。
