PWM转换器小信号建模学习探讨

模型的构建是按下面四个步骤：

第一、电路模拟化（等同平均处理）

第二、小信号扰动，去直流、线性化

第三、Laplace变换

第四、右半平面零点分析

第一步、电路模拟化、去脉动量

通过等效变换将脉动的开关电源转变为连续的模拟电路去分析。开关电源的模拟化表达式就是其直流增益表达式，在CCM模式下Buck电路M=D，boost电路M=1/(1-D)，Buck-Boost电路M=D/(1-D)，用理想可调变压器来替代开关和二极管做等效变换分别如下：

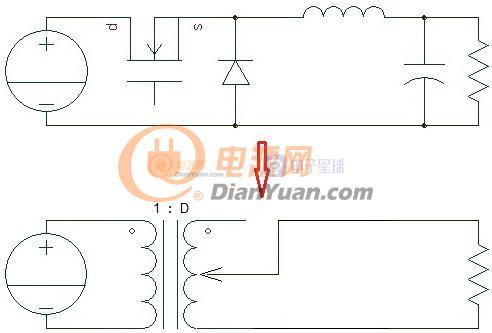
                                           图1-1 Buck电路直流等效电路

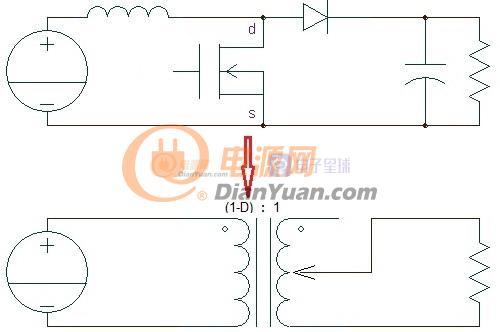
                                        图1-2 Boost电路直流等效电路

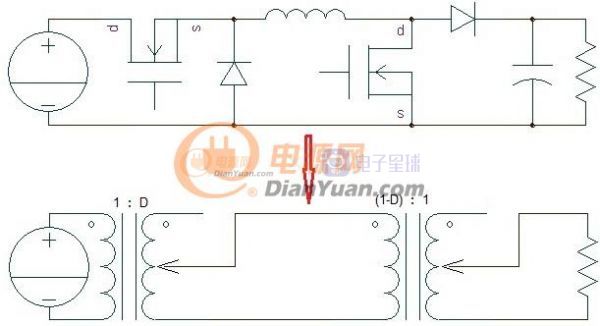
                                       图1-3 Buck-Boost电路直流等效电路

其中Buck-Boost电路采用双开关双二极管结构以便于理解。

借鉴三极管的分析方法上述也可以称之为静态工作点表达式，模拟化分析需要假设脉动量的频率（开关频率）很高才够准确。

第二步、加入小信号扰动，去直流、线性化

时域只反映当下的情况通过频域可以预见之前、之后的情况。已知利用Laplace变换可以实现从时域到频域的转换前提是在线性系统下（非线性系统有时域到频域的变换方法吗？）。

先分析Boost电路（从输出到控制），见下图

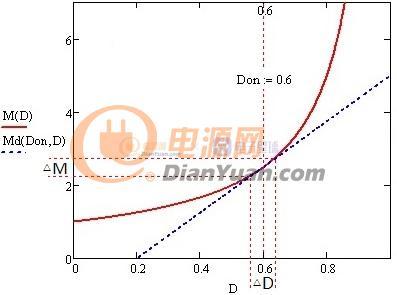
                                   图2-1 Boost小信号扰动

如图2-1在Boost电路的直流增益曲线上加入扰动，如果扰动量△D很小可以近似认为这一小段为线性变化其斜率为直流增益曲线的导数△M/△D=1/(1-D)²。这也是为什么要用小信号来分析的原因，如果扰动量过大当前模型不能做线性近似分析的结果就不准确了。

小信号分析只关注交流量，将图2-1做去除直流处理把交流增益曲线平移至过零点既完成线性化处理，实际运算只需对直流增益求导既可（小信号增益等同扰动增益默认为交流量，下同），见下图2-2。

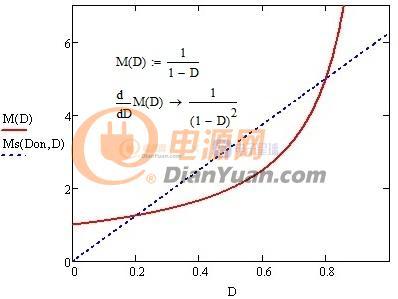
                                   图2-2 Boost线性处理

经上述分析可知非线性系统的交流增益和直流增益是不同的，依此分别列出三种电路的交流小线号等效模型如下：

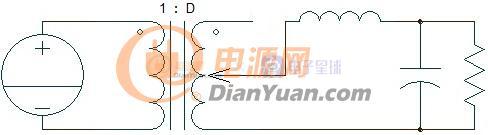
                                       图2-3 Buck交流等效电路

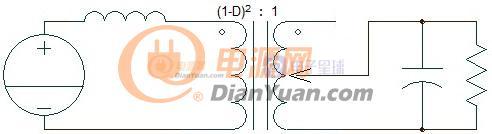
                                        图2-4 Boost交流等效电路

                                         图2-5 Buck-Boost交流等效电路

Buck电路直流增益是线性的所以其交流增益与直流增益相同（Buck电路应当可以承受更大的扰动信号），将初级侧映射到次级后等效输入电压为Vg=Vin*D，后面为LC低通滤波器结构。

Boost电路交流增益为直流增益的平方，将初级侧映射到次级后输入等效电压为Vg=Vin/(1-D)²，等效电感为Le= L/(1-D)²。

Buck-Boost电路可以看做输入等效电压为Vin*D的Boost电路。

第三步、拉氏变换

因为交流小信号已经做了线性化处理，电路也都变成了LC低通滤波这一统一结构，因而可以直接进行拉氏变换只需将电感变为s*L（或s*Le）电容变为1/(s*C)。经拉氏变换后的感抗、容抗可以同普通电阻一样进行串并联组合分析，进而得出频域方程。

第四步、右半平面零点分析

对可调变压器进行扰动后会引发电压、电流及二阶微小量这三个变化量，前面分析中已经用到了电压变化量，二阶微小量因为很小可以忽略，电流的变化会在电感中产生反向电动势阻碍输出电压变化呈现右半平面零点的特性。

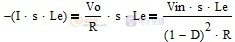         （右半平面零点引发的压降）

对于Buck电路电流的扰动在初级侧，因为有输入电压的钳位不会对电感造成影响所以没有右半平面零点问题。

精彩，感谢分享！

上面4楼第二步的思路可能不对（没有考虑到扰动方向和电路互易性的问题），将大信号和小信号从电路中分离出后得到小信号模型推导如下：

                                    图3-1-1 Buck小信号模型推导

上图中第二步输入电压源作为交流信号的通道时可视为短路，电流的扰动被电压源短路不会对后级电路造成影响。

忽略寄生电阻得到的理想增益表达式如下：

其中Vosc为控制器中锯齿波发生器的峰峰值。仿真验证如下：

                                  图3-1-2 Buck小信号仿真、计算对比

对于扰动信号来说电路具有时时互易性如果自左向右为Boost那么自右向左就为Buck，Boost扰动刚好自右向左为Buck特性，这样就不用做线性处理推导起来容易了许多：

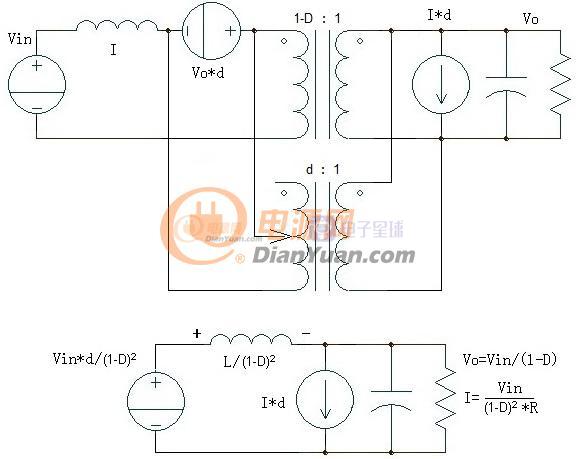
                                       图3-2-1 Boost小信号模型推导

忽略寄生电阻得到的理想增益曲线表达式为：

仿真验证如下：

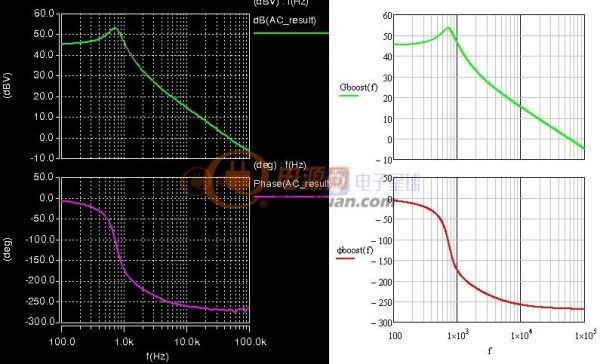
                                   图3-2-2 Boost小信号仿真、计算对比

Buck-Boost的小信号模型如前面分析的一样，将Buck和Boost电路串联起来就可以：

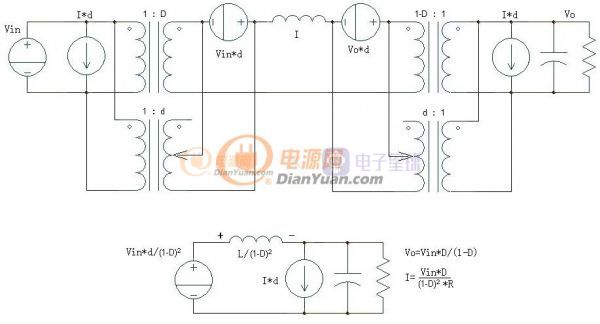
                        图3-3-1 Buck-Boost小信号模型推导

忽略寄生电阻得到的理想增益曲线表达式为：

仿真验证如下：

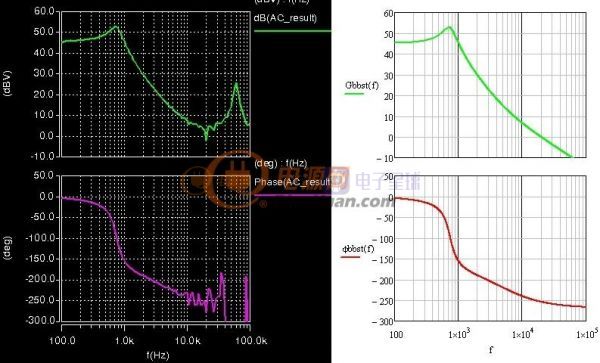
                    图3-3-2 Buck-Boost小信号仿真、计算对比

Buck-Boost与Boost的区别在于直流增益上，带来的影响是右边平面零点不同。

其实这里依然采用的是参考资料中的方法，只不过从繁杂的公式推导中解放出来，采用一种更直观、形象的方式来演示小信号的工作过程。