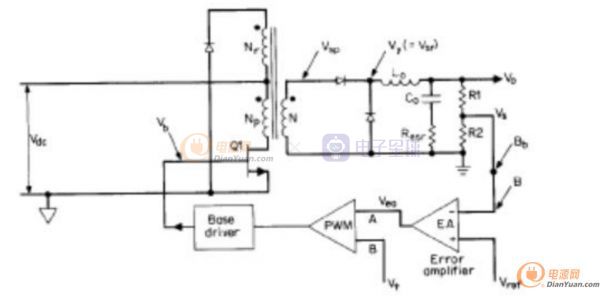
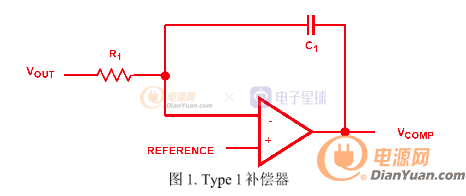
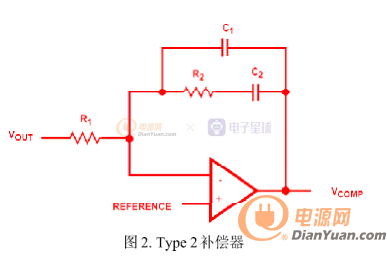
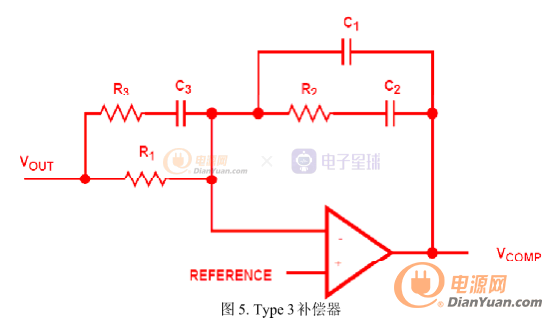
自己着手开关电源环路控制的学习大半个月了,今天开始写<单端正激式开关电源设计之环路控制设计>的帖子,希望大家多多支持.
首先讲讲自己大半个月来学习开关电源环路控制的历程.做开关电源的研发5年多了,一直专注于实践,基本没有怎么钻研过环路控制这一块.
学习环路控制,我首先将<现代控制工程>这本书匆匆翻了三遍,头脑中大至有了系统控制的思想.书中介绍了各种自动控制的思想以及证明解析过程,由于本人的数学底子薄弱,所以对于书中讲解的几种常用的分析方法,比如频域分析法,时域分析法,根轨迹法,波特图法的理解都是浮于表面,惭愧.对环路的学习理解还存在诸多的问题,后续的讲解必然有很多的问题,希望大家能及时指正.
接着买了两本书籍,都是关于开关电源环路分析的书籍.一本是张卫平编写的<开关变换器的建模与仿真>,另一本是法国电源工程师Basso写的<开关电源SPICE仿真与实用设计>.两本书中讲解的关于电源环路控制的知识点个人觉得很不错,虽然我看的云里雾里的,但是书上讲解到的一些我能看懂的部分对我个人对于电源环路控制的理解帮助很大,对于电源的理解也深入了很多.