看了CMG的反激电源设计及应用之六:控制环路设计.
http://bbs.dianyuan.com/topic/4745
开始没有看懂,后来找来一些自动化方面的书看了一下,觉得收获不小,在这里也希望给对这方面有缺陷的朋友们一些帮助.
控制环的基础知识,伯德图
全部回复(16)
正序查看
倒序查看
现在还没有回复呢,说说你的想法
关于控制环的基础知识
传递函数:是经典控制理论最重要的数学模型,它是在拉氏变换法(一种线性积分变换),求解线性常微分方程中引申出来的复数域的数学模型.
它是在线性定常系统中,当初始条件为零时,系统输出复函数与输入复函数的比值,这个比值不依赖于输入输出,它是系统的固有特性.
传递函数本质上是数学模型,在形式上却是一个函数,而不是一个方程.这不但使运算上大为简便,而且可以很方便的用图形表示.这正是工程上广泛采用传递函数分析系统的主要原因.
而伯德图就是一个最常用的频域分析的几何表示法,伯德图(BODE)又称对数频率特性曲线,包括对数幅频曲线和对数相频曲线.如下图,一个PWM开关电源的伯德图.
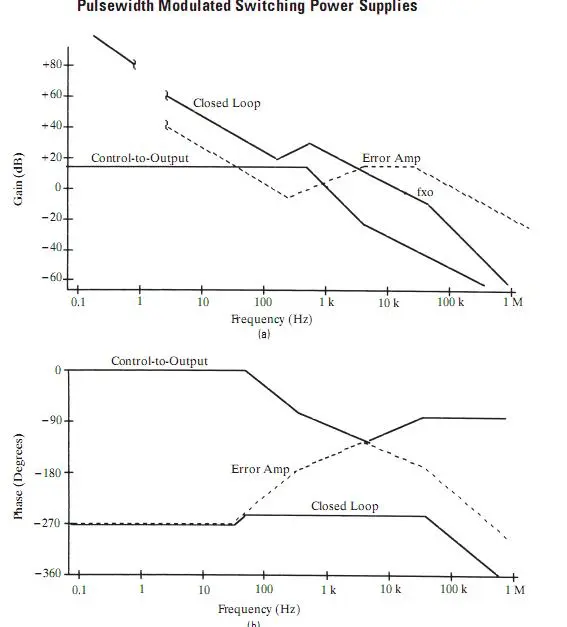 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204028189.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204028189.jpg');}" onmousewheel="return imgzoom(this);">
要了解伯德图,首先要了解频率特性的定义,频率特性是指线性系统在正弦函数的作用下,稳态输出与输入复数符号之比对频率的关系.它是传递函数的特例,也表征了系统的运动规律,可以由下图来理解.
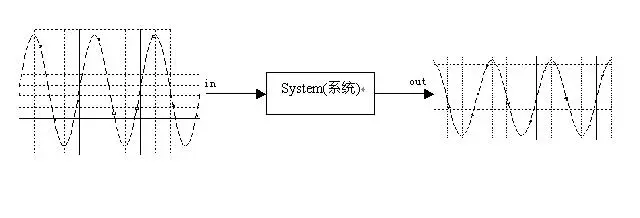 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204028215.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204028215.jpg');}" onmousewheel="return imgzoom(this);">
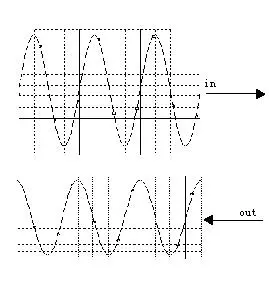 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204028254.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204028254.jpg');}" onmousewheel="return imgzoom(this);">
从上图可以看出,输出相对于输入只是振幅和相位发生了变化,而频率是不变的.而伯德图就是在输入的所有频率上,这里包括我们经常说的低频段、中频段和高频段.对每个频率段取几个点,然后进行运算,算增益,算相位差,再转换成对数,然后就可以在伯德图上面描点,如上图,假如频率为30hz,增益为0.7,相位差为90度,即out的振幅/in的振幅=0.7,out的相位比in的相位滞后了90度.复频曲线,在伯德图上横坐标的30hz的对应的纵坐标的20lg0.7(DB)处可以描到一个点;相频曲线,在30hz对应-90度同样可以描到一个点.这样通过翻杂的描点,可以画出系统的伯德图.
为什么输入的要是一个正炫信号呢?主要是由于他形式简单,对于频域分析的三个要素正好吻合,而且对于系统的数学分析和实验研究是容易实现的.
在我们的电源设计中,在没有补偿之前,只考虑前向通道时(即控制到输出),我们的传递函数称为开环传递函数.
补偿后的系统的传递函数称为闭环传递函数.
下面有讲零极点的问题.
在传递函数中,令分子为零时,得到的频率和增益所对应的点称为零点;
令分母为零时,得到的频率与增益所对应的点称为极点.
EG.
在伯德图中,在零点和极点上,曲线会有一个转折,一般把-20DB/10DEC称为一个极点,把+20DB/10DEC称为一个零点,那么同一频率上的2个零点就是40DB/DEC,以此类推.
传递函数:是经典控制理论最重要的数学模型,它是在拉氏变换法(一种线性积分变换),求解线性常微分方程中引申出来的复数域的数学模型.
它是在线性定常系统中,当初始条件为零时,系统输出复函数与输入复函数的比值,这个比值不依赖于输入输出,它是系统的固有特性.
传递函数本质上是数学模型,在形式上却是一个函数,而不是一个方程.这不但使运算上大为简便,而且可以很方便的用图形表示.这正是工程上广泛采用传递函数分析系统的主要原因.
而伯德图就是一个最常用的频域分析的几何表示法,伯德图(BODE)又称对数频率特性曲线,包括对数幅频曲线和对数相频曲线.如下图,一个PWM开关电源的伯德图.
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204028189.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204028189.jpg');}" onmousewheel="return imgzoom(this);">
要了解伯德图,首先要了解频率特性的定义,频率特性是指线性系统在正弦函数的作用下,稳态输出与输入复数符号之比对频率的关系.它是传递函数的特例,也表征了系统的运动规律,可以由下图来理解.
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204028215.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204028215.jpg');}" onmousewheel="return imgzoom(this);">
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204028254.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204028254.jpg');}" onmousewheel="return imgzoom(this);">
从上图可以看出,输出相对于输入只是振幅和相位发生了变化,而频率是不变的.而伯德图就是在输入的所有频率上,这里包括我们经常说的低频段、中频段和高频段.对每个频率段取几个点,然后进行运算,算增益,算相位差,再转换成对数,然后就可以在伯德图上面描点,如上图,假如频率为30hz,增益为0.7,相位差为90度,即out的振幅/in的振幅=0.7,out的相位比in的相位滞后了90度.复频曲线,在伯德图上横坐标的30hz的对应的纵坐标的20lg0.7(DB)处可以描到一个点;相频曲线,在30hz对应-90度同样可以描到一个点.这样通过翻杂的描点,可以画出系统的伯德图.
为什么输入的要是一个正炫信号呢?主要是由于他形式简单,对于频域分析的三个要素正好吻合,而且对于系统的数学分析和实验研究是容易实现的.
在我们的电源设计中,在没有补偿之前,只考虑前向通道时(即控制到输出),我们的传递函数称为开环传递函数.
补偿后的系统的传递函数称为闭环传递函数.
下面有讲零极点的问题.
在传递函数中,令分子为零时,得到的频率和增益所对应的点称为零点;
令分母为零时,得到的频率与增益所对应的点称为极点.
EG.
在伯德图中,在零点和极点上,曲线会有一个转折,一般把-20DB/10DEC称为一个极点,把+20DB/10DEC称为一个零点,那么同一频率上的2个零点就是40DB/DEC,以此类推.
0
回复
提示
@einfen
关于控制环的基础知识传递函数:是经典控制理论最重要的数学模型,它是在拉氏变换法(一种线性积分变换),求解线性常微分方程中引申出来的复数域的数学模型.它是在线性定常系统中,当初始条件为零时,系统输出复函数与输入复函数的比值,这个比值不依赖于输入输出,它是系统的固有特性.传递函数本质上是数学模型,在形式上却是一个函数,而不是一个方程.这不但使运算上大为简便,而且可以很方便的用图形表示.这正是工程上广泛采用传递函数分析系统的主要原因.而伯德图就是一个最常用的频域分析的几何表示法,伯德图(BODE)又称对数频率特性曲线,包括对数幅频曲线和对数相频曲线.如下图,一个PWM开关电源的伯德图.[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204028189.jpg');}"onmousewheel="returnimgzoom(this);">要了解伯德图,首先要了解频率特性的定义,频率特性是指线性系统在正弦函数的作用下,稳态输出与输入复数符号之比对频率的关系.它是传递函数的特例,也表征了系统的运动规律,可以由下图来理解.[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204028215.jpg');}"onmousewheel="returnimgzoom(this);">[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204028254.jpg');}"onmousewheel="returnimgzoom(this);">从上图可以看出,输出相对于输入只是振幅和相位发生了变化,而频率是不变的.而伯德图就是在输入的所有频率上,这里包括我们经常说的低频段、中频段和高频段.对每个频率段取几个点,然后进行运算,算增益,算相位差,再转换成对数,然后就可以在伯德图上面描点,如上图,假如频率为30hz,增益为0.7,相位差为90度,即out的振幅/in的振幅=0.7,out的相位比in的相位滞后了90度.复频曲线,在伯德图上横坐标的30hz的对应的纵坐标的20lg0.7(DB)处可以描到一个点;相频曲线,在30hz对应-90度同样可以描到一个点.这样通过翻杂的描点,可以画出系统的伯德图.为什么输入的要是一个正炫信号呢?主要是由于他形式简单,对于频域分析的三个要素正好吻合,而且对于系统的数学分析和实验研究是容易实现的.在我们的电源设计中,在没有补偿之前,只考虑前向通道时(即控制到输出),我们的传递函数称为开环传递函数.补偿后的系统的传递函数称为闭环传递函数.下面有讲零极点的问题.在传递函数中,令分子为零时,得到的频率和增益所对应的点称为零点; 令分母为零时,得到的频率与增益所对应的点称为极点.EG.在伯德图中,在零点和极点上,曲线会有一个转折,一般把-20DB/10DEC称为一个极点,把+20DB/10DEC称为一个零点,那么同一频率上的2个零点就是40DB/DEC,以此类推.
顶!兄弟不错,知其然知其所以然.顶了!
0
回复
提示
@chernwenbin
顶!兄弟不错,知其然知其所以然.顶了!
下面有两个例子,是最基本的积分环节和微分环节.
微分环节:
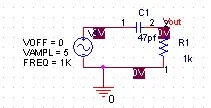 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204116508.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204116508.jpg');}" onmousewheel="return imgzoom(this);">
C(s)/R(s)=G(s)=Tdr(t)/dt=Ts ,s出现在分子中,令分子为零,得到一个零点,即增益以20DB/10DEC的斜率上升.
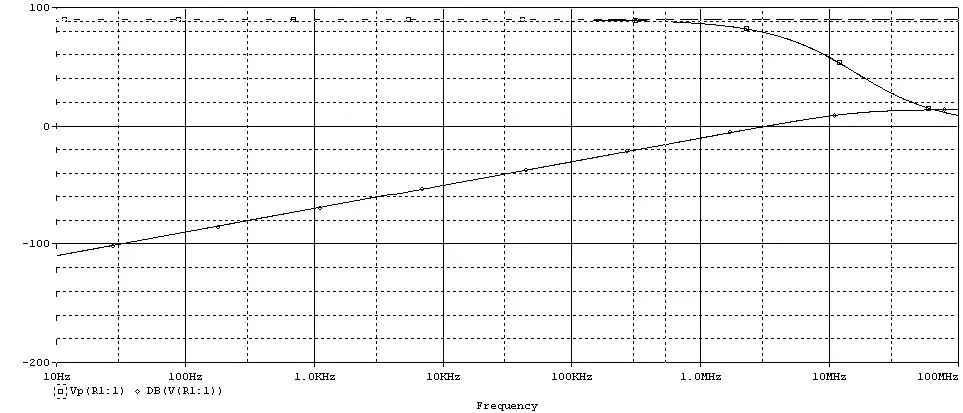 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204116611.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204116611.jpg');}" onmousewheel="return imgzoom(this);">
可见在1MHZ以下,增益是一条以20DB/10DEC的斜率上升的直线,而相位始终是90度.
积分环节:
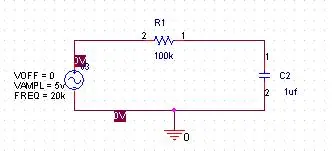 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204116648.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204116648.jpg');}" onmousewheel="return imgzoom(this);">
C(s)/R(s)=G(s)=1/T*INT(r(t))=1/Ts ,s出现在分母中,令分母为零,得到一个极点,即增益以20DB/10DEC的斜率下降.
微分环节:
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204116508.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204116508.jpg');}" onmousewheel="return imgzoom(this);">
C(s)/R(s)=G(s)=Tdr(t)/dt=Ts ,s出现在分子中,令分子为零,得到一个零点,即增益以20DB/10DEC的斜率上升.
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204116611.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204116611.jpg');}" onmousewheel="return imgzoom(this);">
可见在1MHZ以下,增益是一条以20DB/10DEC的斜率上升的直线,而相位始终是90度.
积分环节:
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204116648.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204116648.jpg');}" onmousewheel="return imgzoom(this);">
C(s)/R(s)=G(s)=1/T*INT(r(t))=1/Ts ,s出现在分母中,令分母为零,得到一个极点,即增益以20DB/10DEC的斜率下降.
0
回复
提示
@einfen
下面有两个例子,是最基本的积分环节和微分环节.微分环节:[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204116508.jpg');}"onmousewheel="returnimgzoom(this);">C(s)/R(s)=G(s)=Tdr(t)/dt=Ts,s出现在分子中,令分子为零,得到一个零点,即增益以20DB/10DEC的斜率上升.[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204116611.jpg');}"onmousewheel="returnimgzoom(this);">可见在1MHZ以下,增益是一条以20DB/10DEC的斜率上升的直线,而相位始终是90度.积分环节:[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204116648.jpg');}"onmousewheel="returnimgzoom(this);">C(s)/R(s)=G(s)=1/T*INT(r(t))=1/Ts,s出现在分母中,令分母为零,得到一个极点,即增益以20DB/10DEC的斜率下降.
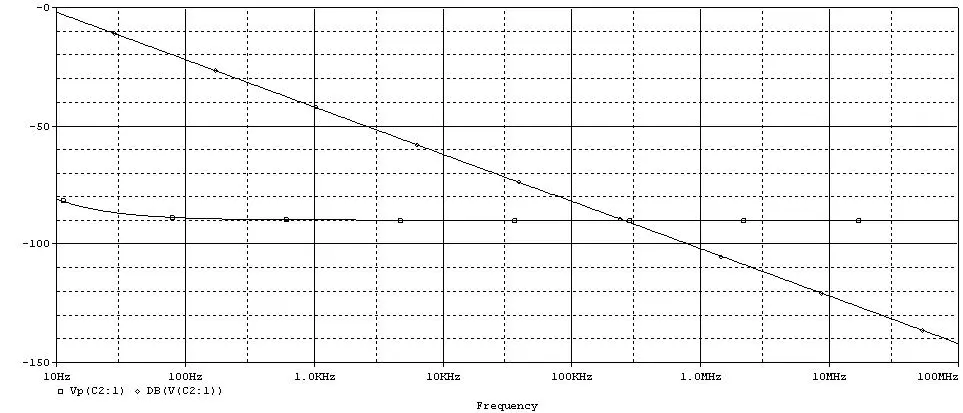 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204117162.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/62/1897031204117162.jpg');}" onmousewheel="return imgzoom(this);">
可见在100HZ以上,增益是一条以20DB/10DEC的斜率下降的直线,而相位始终是-90度.
伯德图很好的解决了把乘法转化为加法的运算,在图形中表现出来,因为lgA+lgB=lgA*B,这样很利于作图,从上面的图形中可以看出out-control+error amp=close loop
0
回复
提示
@einfen
[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204117162.jpg');}"onmousewheel="returnimgzoom(this);">可见在100HZ以上,增益是一条以20DB/10DEC的斜率下降的直线,而相位始终是-90度.伯德图很好的解决了把乘法转化为加法的运算,在图形中表现出来,因为lgA+lgB=lgA*B,这样很利于作图,从上面的图形中可以看出out-control+erroramp=closeloop
似乎是个冷门?
0
回复
提示
@einfen
[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204117162.jpg');}"onmousewheel="returnimgzoom(this);">可见在100HZ以上,增益是一条以20DB/10DEC的斜率下降的直线,而相位始终是-90度.伯德图很好的解决了把乘法转化为加法的运算,在图形中表现出来,因为lgA+lgB=lgA*B,这样很利于作图,从上面的图形中可以看出out-control+erroramp=closeloop
一直知道有博得图,今天终于搞清了是怎么回事。
以前我是做通信的,现在看了伯德图,原来它就是通信上一直用的幅频曲线和相频曲线啊。不过估计他们在用法上还是有一些区别,搬凳子,继续听讲。
0
回复
提示
@einfen
关于控制环的基础知识传递函数:是经典控制理论最重要的数学模型,它是在拉氏变换法(一种线性积分变换),求解线性常微分方程中引申出来的复数域的数学模型.它是在线性定常系统中,当初始条件为零时,系统输出复函数与输入复函数的比值,这个比值不依赖于输入输出,它是系统的固有特性.传递函数本质上是数学模型,在形式上却是一个函数,而不是一个方程.这不但使运算上大为简便,而且可以很方便的用图形表示.这正是工程上广泛采用传递函数分析系统的主要原因.而伯德图就是一个最常用的频域分析的几何表示法,伯德图(BODE)又称对数频率特性曲线,包括对数幅频曲线和对数相频曲线.如下图,一个PWM开关电源的伯德图.[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204028189.jpg');}"onmousewheel="returnimgzoom(this);">要了解伯德图,首先要了解频率特性的定义,频率特性是指线性系统在正弦函数的作用下,稳态输出与输入复数符号之比对频率的关系.它是传递函数的特例,也表征了系统的运动规律,可以由下图来理解.[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204028215.jpg');}"onmousewheel="returnimgzoom(this);">[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204028254.jpg');}"onmousewheel="returnimgzoom(this);">从上图可以看出,输出相对于输入只是振幅和相位发生了变化,而频率是不变的.而伯德图就是在输入的所有频率上,这里包括我们经常说的低频段、中频段和高频段.对每个频率段取几个点,然后进行运算,算增益,算相位差,再转换成对数,然后就可以在伯德图上面描点,如上图,假如频率为30hz,增益为0.7,相位差为90度,即out的振幅/in的振幅=0.7,out的相位比in的相位滞后了90度.复频曲线,在伯德图上横坐标的30hz的对应的纵坐标的20lg0.7(DB)处可以描到一个点;相频曲线,在30hz对应-90度同样可以描到一个点.这样通过翻杂的描点,可以画出系统的伯德图.为什么输入的要是一个正炫信号呢?主要是由于他形式简单,对于频域分析的三个要素正好吻合,而且对于系统的数学分析和实验研究是容易实现的.在我们的电源设计中,在没有补偿之前,只考虑前向通道时(即控制到输出),我们的传递函数称为开环传递函数.补偿后的系统的传递函数称为闭环传递函数.下面有讲零极点的问题.在传递函数中,令分子为零时,得到的频率和增益所对应的点称为零点; 令分母为零时,得到的频率与增益所对应的点称为极点.EG.在伯德图中,在零点和极点上,曲线会有一个转折,一般把-20DB/10DEC称为一个极点,把+20DB/10DEC称为一个零点,那么同一频率上的2个零点就是40DB/DEC,以此类推.
有时电路的传递函数不太容易写出来,该怎样获得伯德图呢?求指点
0
回复
提示
@einfen
[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204117162.jpg');}"onmousewheel="returnimgzoom(this);">可见在100HZ以上,增益是一条以20DB/10DEC的斜率下降的直线,而相位始终是-90度.伯德图很好的解决了把乘法转化为加法的运算,在图形中表现出来,因为lgA+lgB=lgA*B,这样很利于作图,从上面的图形中可以看出out-control+erroramp=closeloop
为什么是在100HZ左右呢?如果没有这个图的话,怎么能通过理论知道这个100HZ频率点阿?包括上面说的1MHZ频率点?
0
回复
提示
@einfen
[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204117162.jpg');}"onmousewheel="returnimgzoom(this);">可见在100HZ以上,增益是一条以20DB/10DEC的斜率下降的直线,而相位始终是-90度.伯德图很好的解决了把乘法转化为加法的运算,在图形中表现出来,因为lgA+lgB=lgA*B,这样很利于作图,从上面的图形中可以看出out-control+erroramp=closeloop
听不懂啊,,,,,,,,,,,![]()
0
回复
提示
@einfen
关于控制环的基础知识传递函数:是经典控制理论最重要的数学模型,它是在拉氏变换法(一种线性积分变换),求解线性常微分方程中引申出来的复数域的数学模型.它是在线性定常系统中,当初始条件为零时,系统输出复函数与输入复函数的比值,这个比值不依赖于输入输出,它是系统的固有特性.传递函数本质上是数学模型,在形式上却是一个函数,而不是一个方程.这不但使运算上大为简便,而且可以很方便的用图形表示.这正是工程上广泛采用传递函数分析系统的主要原因.而伯德图就是一个最常用的频域分析的几何表示法,伯德图(BODE)又称对数频率特性曲线,包括对数幅频曲线和对数相频曲线.如下图,一个PWM开关电源的伯德图.[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204028189.jpg');}"onmousewheel="returnimgzoom(this);">要了解伯德图,首先要了解频率特性的定义,频率特性是指线性系统在正弦函数的作用下,稳态输出与输入复数符号之比对频率的关系.它是传递函数的特例,也表征了系统的运动规律,可以由下图来理解.[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204028215.jpg');}"onmousewheel="returnimgzoom(this);">[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204028254.jpg');}"onmousewheel="returnimgzoom(this);">从上图可以看出,输出相对于输入只是振幅和相位发生了变化,而频率是不变的.而伯德图就是在输入的所有频率上,这里包括我们经常说的低频段、中频段和高频段.对每个频率段取几个点,然后进行运算,算增益,算相位差,再转换成对数,然后就可以在伯德图上面描点,如上图,假如频率为30hz,增益为0.7,相位差为90度,即out的振幅/in的振幅=0.7,out的相位比in的相位滞后了90度.复频曲线,在伯德图上横坐标的30hz的对应的纵坐标的20lg0.7(DB)处可以描到一个点;相频曲线,在30hz对应-90度同样可以描到一个点.这样通过翻杂的描点,可以画出系统的伯德图.为什么输入的要是一个正炫信号呢?主要是由于他形式简单,对于频域分析的三个要素正好吻合,而且对于系统的数学分析和实验研究是容易实现的.在我们的电源设计中,在没有补偿之前,只考虑前向通道时(即控制到输出),我们的传递函数称为开环传递函数.补偿后的系统的传递函数称为闭环传递函数.下面有讲零极点的问题.在传递函数中,令分子为零时,得到的频率和增益所对应的点称为零点; 令分母为零时,得到的频率与增益所对应的点称为极点.EG.在伯德图中,在零点和极点上,曲线会有一个转折,一般把-20DB/10DEC称为一个极点,把+20DB/10DEC称为一个零点,那么同一频率上的2个零点就是40DB/DEC,以此类推.
学习了!
针对文中“假如频率为30hz,增益为0.7,相位差为90度,即out的振幅/in的振幅=0.7,out的相位比in的相位滞后了90度”。给出一点自己的看法。
我们知道L=20lgA---(书上公式),其中A是放大倍数,即幅值放大倍数,增益指的是放大倍数的20倍对数表达方式。所以文中应该描述成“假如频率为30hz,放大倍数为0.7,相位差为90度,即out的振幅/in的振幅=0.7,out的相位比in的相位滞后了90度”更合适吧?
小弟拙见,供参考。
0
回复
提示
@einfen
关于控制环的基础知识传递函数:是经典控制理论最重要的数学模型,它是在拉氏变换法(一种线性积分变换),求解线性常微分方程中引申出来的复数域的数学模型.它是在线性定常系统中,当初始条件为零时,系统输出复函数与输入复函数的比值,这个比值不依赖于输入输出,它是系统的固有特性.传递函数本质上是数学模型,在形式上却是一个函数,而不是一个方程.这不但使运算上大为简便,而且可以很方便的用图形表示.这正是工程上广泛采用传递函数分析系统的主要原因.而伯德图就是一个最常用的频域分析的几何表示法,伯德图(BODE)又称对数频率特性曲线,包括对数幅频曲线和对数相频曲线.如下图,一个PWM开关电源的伯德图.[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204028189.jpg');}"onmousewheel="returnimgzoom(this);">要了解伯德图,首先要了解频率特性的定义,频率特性是指线性系统在正弦函数的作用下,稳态输出与输入复数符号之比对频率的关系.它是传递函数的特例,也表征了系统的运动规律,可以由下图来理解.[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204028215.jpg');}"onmousewheel="returnimgzoom(this);">[图片]500){this.resized=true;this.width=500;this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}"onclick="if(!this.resized){returntrue;}else{window.open('http://u.dianyuan.com/bbs/u/62/1897031204028254.jpg');}"onmousewheel="returnimgzoom(this);">从上图可以看出,输出相对于输入只是振幅和相位发生了变化,而频率是不变的.而伯德图就是在输入的所有频率上,这里包括我们经常说的低频段、中频段和高频段.对每个频率段取几个点,然后进行运算,算增益,算相位差,再转换成对数,然后就可以在伯德图上面描点,如上图,假如频率为30hz,增益为0.7,相位差为90度,即out的振幅/in的振幅=0.7,out的相位比in的相位滞后了90度.复频曲线,在伯德图上横坐标的30hz的对应的纵坐标的20lg0.7(DB)处可以描到一个点;相频曲线,在30hz对应-90度同样可以描到一个点.这样通过翻杂的描点,可以画出系统的伯德图.为什么输入的要是一个正炫信号呢?主要是由于他形式简单,对于频域分析的三个要素正好吻合,而且对于系统的数学分析和实验研究是容易实现的.在我们的电源设计中,在没有补偿之前,只考虑前向通道时(即控制到输出),我们的传递函数称为开环传递函数.补偿后的系统的传递函数称为闭环传递函数.下面有讲零极点的问题.在传递函数中,令分子为零时,得到的频率和增益所对应的点称为零点; 令分母为零时,得到的频率与增益所对应的点称为极点.EG.在伯德图中,在零点和极点上,曲线会有一个转折,一般把-20DB/10DEC称为一个极点,把+20DB/10DEC称为一个零点,那么同一频率上的2个零点就是40DB/DEC,以此类推.
讲得很好!
0
回复
提示

