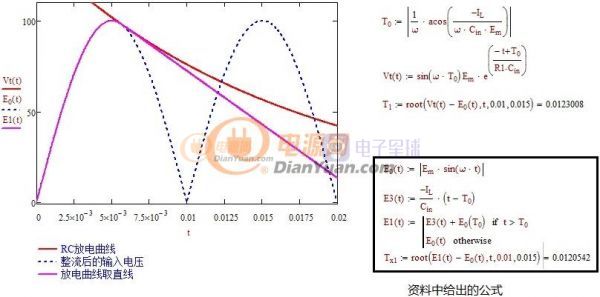
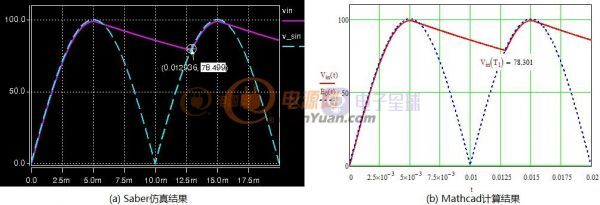
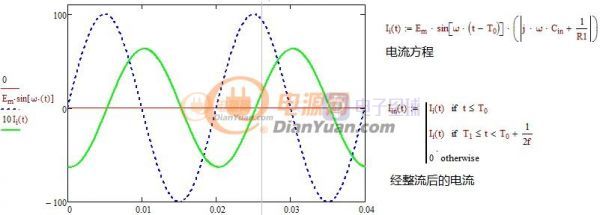
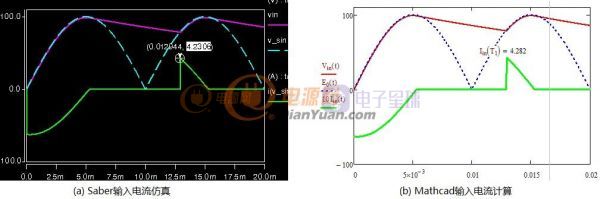
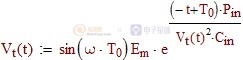反激的设计资料多是以公式的方式表述不够形象,所以想用图形的方式将公式表述出来。
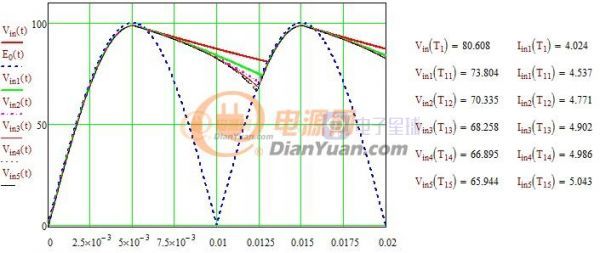
比如设计匝比时先确定占空比还是先确定反射电压?见下图(Vmax=300,Vmin=100,Vo=5,f=60KHz)
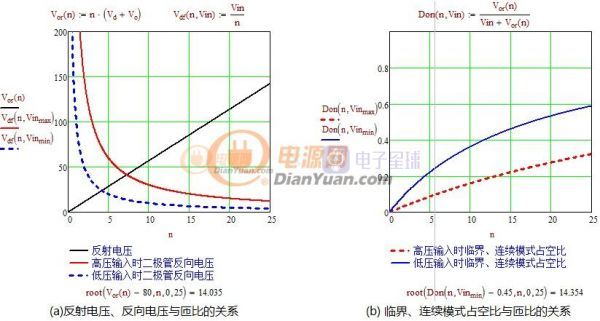
图1-1 反射电压、占空比与匝比的关系
图(a)是反射电压、输出二极管反向电压与匝比的关系,匝比越大反射电压越高输出二极管反向电压越小。
图(b)是临界、连续模式时占空比与匝比的关系,匝比越大临界、连续模式的占空比越大。
占空比和反射电压二者是相互关联的,从上图可以通过直观的对比来选则一个匝比数比如取n=14,此时反射电压Vor≈80V,占空比D≈0.45。如果匝比取n=21,此时反射电压Vor≈120V,占空比D≈0.55,后者的效率会高一些不过需斜坡补偿。后面再讨论用图形法分析斜坡补偿和效率的问题。
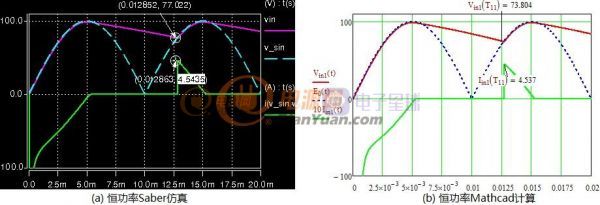
再比如上面的例子,分别取电感L=600uH和电感L=420uH,在匝比n=14的条件下看临界功率曲线.
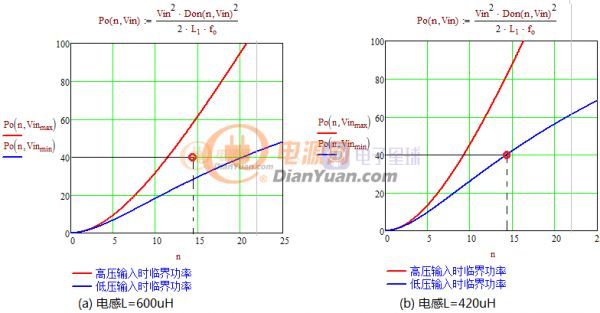
图1-2 临界功率曲线与匝比的关系
假设输出功率为40W,图(a)电感L=600uH低压输入时连续模式高压输入时断续模式,图(b)L=420uH全程工作于临界或断续模式。
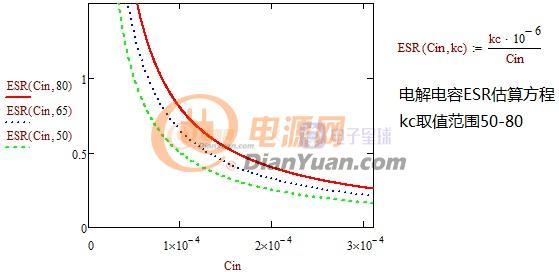
后续的图解分析大概包括变压器设计、电容选取、纹波、小信号、效率分析、EMI设计等,期望能从这个过程中找出最优参数的设计方法。