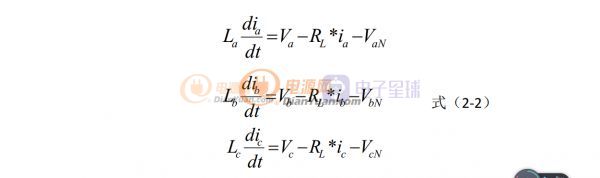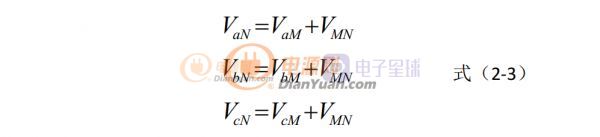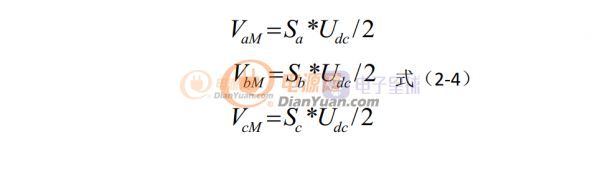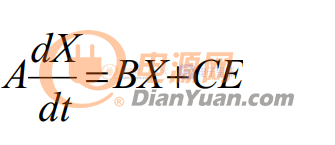新能源汽车充电模块之Vienna整流

一．技术背景及研究意义

新能源汽车是未来的发展趋势，充电桩的建设已纳入到市政建设中，新建小区必须预留充电桩建设位置，充电桩的前景将会越来越好，在最近几年也将要迎来爆发期，我们今天要探究的VIENNA整流技术，是新能源充电桩模块上主要拓扑结构之一，已经很成熟和广泛的应用在7.5KW，12KW，15KW等系列充电模块上。

上个世纪90年代初，VIENNA大学的J.W.Kolar等提出了一种新型的整流器拓扑，即VIENNA整流器,VIENNA整流器具有以下特点：

1) 类似于Boost型PFC整流器，可以实现输入电流正弦跟随输入电压，波形畸变率低，能够实现整流器功率因数PF->1。

2)功率MOS管、功率二极管等器件上所承受电压应力低，理论上最大电压Vrm为直流输出电压的一半。

3)相较于普通两电平全桥整理器，在相同的开关频率下电感的电流纹波降低，因而减小了电感的体积，提高了整流器的功率密度。

4)功率开关管与上、下桥臂的二极管串联，因此不会因为开关管的误导通造成桥臂的直通从而烧毁器件，因此具有较高的可靠性。

按是否有中性线连接，三相VIENNA整流器可分为三相四线制及三相三线制，在三相四线制VIENNA整流器中，用中性线将输入侧中性点与电容中点连接,则整流器可解耦为三个单相BOOST拓扑，由于中性线的引入,在实际应用中会给设计带来困难并且限制了应用场合，在充电模块上实际应用的是三相三线VIENNA整流器。

二．数学模型和控制框图

2.1 VIENNA 整流器拓扑结构分析

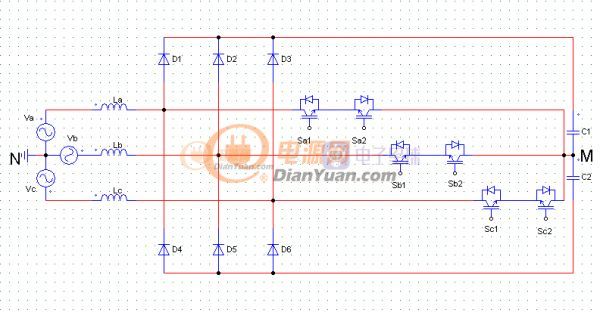
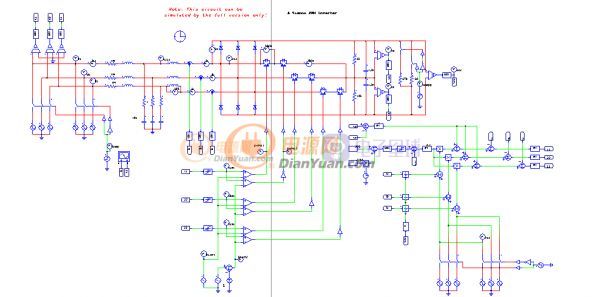
三相 VIENNA 整流器拓扑结构如图 2-1 所示，采用三相三线制的型式，连接电容中点 M 和中性点 N 就构成了三相四线制结构。其中， Va、 Vb、 Vc为三相对称的三相电源， La、 Lb、 Lc 为三相升压电感， D1、D2、D3、D4、D5、D6为续流二极管，功率器件 Sa1、 Sb1、 Sc1、Sa2、 Sb2、 Sc2 连接于整流器输入端和直流母线电容中点，每个开关管有开通和关断两种状态。

图2-1

2.2 VIENNA 整流器工作原理及开关状态分析

VIENNA 整流器的工作原理与开关管的状态及电源侧电流方向有关，每一相桥臂都可以等效为一个正向和反向 Boost 电路。三相三线制结构流入 M 点的一相电流通过另外两相构成回路。现以一相电流流通路径为例，另两相与之相同，以下根据电网电压极性，分两种情况进行讨论：

电网电压为正半周时

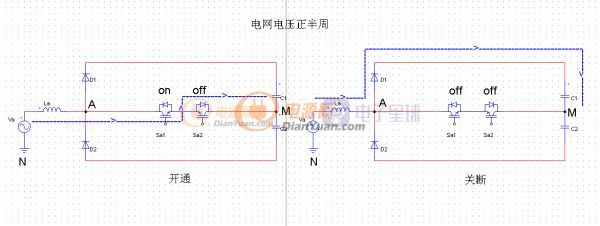
在电网电压为正半周，开关导通和关断的时候，每一相桥臂上电流的流通路径分别如图 2-2 中箭头所示。

图2-2

当开关管 Sa1 导通时，电流通过 Sa1，Sa2 至电容中点M，该过程中电压 Va>0，电流不断地增大对电感 La 进行储能，此时 A 点相对于电容中点M电位为 0。当开关 Sa1 关断后，电流通过续流二极管 D1续流，电感释放能量，对电容 C1 充电， A 点相对电容中点M电位为 1/2Vdc。这一过程相当于一个 Boost电路的充放电过程。

电网电压为负半周时

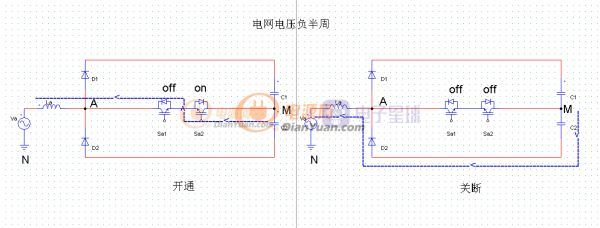
在电网电压为负半周，开关导通和关断的时候，每一个桥臂上电流的流通路径如图 2-3 中箭头所示：

图2-3

当开关管 Sa2 导通时， A 点电位被钳位至电容中点 M， A 点对中点电位为0。当开关 Sa2 关断后，电流通过续流二极管 D2续流，A 点对中点电位为-1/2Vdc。这一过程相当于一个反向 Boost 电路。

2.3基于三相静止坐标下的数学模型

由 VIENNA 整流器的工作原理可知，通过控制每个桥臂功率开关管的通断并结合电流方向，每相交流侧都有 1/2Vdc 、 -1/2Vdc、 0 三种电平状态。定义开关函数，设 Si ( i= a， b ， c)为第 i 相的开关函数，可表示为

将开关函数 Si 分解为 Sip、 Sio、 Sin，3 个单支开关。根据开关管的导通情况和电流的方向有以下关系式成立：若 Si=1，则 Sip=1， Sio=0， Sin=0；若 Si=0，则 Sip=0， Sio =1， Sin =0；若 Si=-1，则 Sip=0， Sio =0， Sin =1。显而易见开关满足如下约束关系： Sip+Sio+Sin =1；

简化之后 VIENNA 整流器的等效电路图如图 2-4 所示

图2-4

根据三电平整流桥主电路，由 KVL 定律，可以得到下面的等式

式中，La,Lb,Lc为整流桥交流侧电感， RL为交流侧等效电阻， Va,Vb,Vc分别为电网三相交流电压，ia,ib,ic 为电网三相交流电流，VaN,VbN,VcN分别为整流桥交流输入端对交流电源N 的电压，可以表示为：

式（2-3）式中， VaM ， VbM ， VcM分别为整流桥三相桥臂交流输入端对输出中点 M 的电压， VMN 为输出母线中点 M 对中性点 N 的电压。由开关函数的定义和电路图可得交流侧电压

三相对称时，有下列恒等关系式

由式(2-2)、 (2-3)、 (2-4)、 (2-5)，可得

对图 2-4 中直流侧的 P 点，应用 Kirchhoff 电流定律，得到

同理对图2-3中的n点，有

对图2-3中的M点，有：

即为

由式(2-6)加减式(2-7)得直流侧回路，有在满足三相电网电压对称的时候，得到在 abc 坐标系下 VIENNA 整流器的数学模型表达式

，表示为矩阵

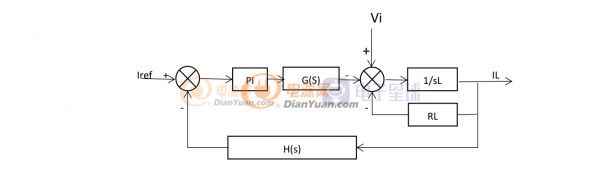
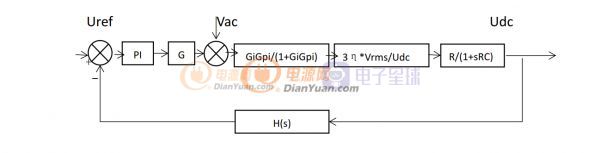
用了这么多公式总算得到三相静止坐标系下 VIENNA 整流器的数学模型，数学模型有什么作用？最终的目的就是指导我们设计闭环控制环路补偿。有了数学模型就可以建立VIENNA 整流器小信号交流模型，最后得到系统开环传递函数，根据开环传递函数就可以进行补偿网络设计，具体方法可以参考学习一下浙大徐德鸿的《电力电子系统建模和控制》一书，本文不做重点推导，后续文章做相关描述。

全部回复(6)

只看楼主

正序查看

倒序查看

jiluo2018

LV.1

2018-10-15 16:22

2.4整流器的环路控制

电压外环电流内环的双闭环控制是目前应用最广泛，最为实用的控制方式。电压外环的输出作为电流指令信号，电流内环用数字PI控制输入电流，使之快速地跟踪电流指令。我们知道，PI控制交流信号会有一定的静差，这一点PR控制会好很多，但是我们的整流器主要是用作整流，为后级提供能量和PFC功能，对电流的静差没有要求，所以这是一个很好的控制策略。本文就双环PI控制和三相SPWM调制结合建立仿真模型。

电流内环控制框图可以简单如下显示

控制框图中PI环节即为数字控制里要设计的补偿环路。

电压外环设计如下由交流小信号模型设计:

其中η为效率，又有电压外环控制框图可以简单如下显示

正负母线电压平衡设计

补偿其调节所得值加入三相电流参考端作为给定电流一部分，然后与三相电流反馈值进行PI调节。

三．仿真模型和波形分析

仿真分析对实际设计起到重要的指导作用。用PSIM软件对电力电子模型进行分析、研究，开发能提高分析速度、分析精度和分析广度。比真实电路实验可扩大研究范围，获取更多数据，也可测一些实验中无法直接测量的数据。仿真进行充分可行性论证后再定购贵重、特殊元件，既节省资金又缩短开发过程，提高产品的质量，最后仿真系统代替实验可大大减少元器件损坏引起的损失，下面就 SPWM 的 VIENNA 整流器系统进行 PSIM 仿真研究。

3.1VIENNA 整流器总体仿真模型

VIENNA 整流系统仿真结构图如下

仿真中设置三角载波频率 50kHz ，采样频率50KHz，电路参数交流电感量0.33mH，正负母线电容量1.2mH。具体选型本文不做重点推导。

3.2静态波形

图3-1 20%载3KW输出电流波形和电感电流波形

图3-2 50%载7.5KW输出电流波形和电感电流波形

图3-3 100%载15KW输出电流波形和电感电流波形

图3-4 母线电压800V和交流线电压Vab

图3-5 输入电压电流PF=99.8%和交流电感电压VPL

3.3动态波形

图3-6 软启动母线电压给定Vref和实际电压Vdc

图3-7 上下母线Vp，Vn不平衡和造成的畸变电流ia在t=0.2s加入中点平衡控制，两母线电压都稳定在400V，电网电流THD会变差。

图3-8 在t=0.25s时由20%载突加至满载电流波形和母线电压波形，电压有20V左右跌落

图3-9 在t=0.25s时由满载载突减至20%载电流波形和母线电压波形，电压有20V左右过冲

图3-10 在t=0.25s时电网电压由220V突降至150V输入电流突然变大，母线电压由5V左右跌落

图3-11 在t=0.25s时电网电压由220V突升至260V输入电流突然变小，母线电压由2V左右突升

本节用PSIM搭建了系统的总体仿真模型，从理论上验证了 VIENNA 整流电路不但有功率因数校正功能，而且有很好的静态性能和动态性能，具有一定的实用价值。 3.4总结未来新能源充电技术将朝着大功率、高功率因数、高效率、低谐波、体积小方向发展。本文通过对Vienna整流器的分析和仿真，全面解释其工作原理和优势，限于本人水平有限，就写到这里，后续再做相关技术探讨，此文抛砖引玉，还望各位专家不吝指正，若觉得本文有可鉴之处，关注我的公众号Exdry艾昌德瑞电子科技，欢迎下载本文和相关仿真模型！

jiluo2018

LV.1

2018-10-15 16:38

@jiluo2018

2.4整流器的环路控制电压外环电流内环的双闭环控制是目前应用最广泛，最为实用的控制方式。电压外环的输出作为电流指令信号，电流内环用数字PI控制输入电流，使之快速地跟踪电流指令。我们知道，PI控制交流信号会有一定的静差，这一点PR控制会好很多，但是我们的整流器主要是用作整流，为后级提供能量和PFC功能，对电流的静差没有要求，所以这是一个很好的控制策略。本文就双环PI控制和三相SPWM调制结合建立仿真模型。电流内环控制框图可以简单如下显示 [图片] 控制框图中PI环节即为数字控制里要设计的补偿环路。电压外环设计如下由交流小信号模型设计: [图片] 其中η为效率，又有电压外环控制框图可以简单如下显示[图片] 正负母线电压平衡设计[图片] 补偿其调节所得值加入三相电流参考端作为给定电流一部分，然后与三相电流反馈值进行PI调节。三．仿真模型和波形分析仿真分析对实际设计起到重要的指导作用。用PSIM软件对电力电子模型进行分析、研究，开发能提高分析速度、分析精度和分析广度。比真实电路实验可扩大研究范围，获取更多数据，也可测一些实验中无法直接测量的数据。仿真进行充分可行性论证后再定购贵重、特殊元件，既节省资金又缩短开发过程，提高产品的质量，最后仿真系统代替实验可大大减少元器件损坏引起的损失，下面就SPWM的VIENNA整流器系统进行PSIM仿真研究。 3.1VIENNA整流器总体仿真模型 VIENNA整流系统仿真结构图如下 [图片] 仿真中设置三角载波频率50kHz，采样频率50KHz，电路参数交流电感量0.33mH，正负母线电容量1.2mH。具体选型本文不做重点推导。 3.2静态波形[图片] 图3-120%载3KW输出电流波形和电感电流波形[图片] 图3-250%载7.5KW输出电流波形和电感电流波形[图片] 图3-3100%载15KW输出电流波形和电感电流波形[图片] 图3-4母线电压800V和交流线电压Vab[图片] 图3-5输入电压电流PF=99.8%和交流电感电压VPL 3.3动态波形[图片] 图3-6软启动母线电压给定Vref和实际电压Vdc[图片] 图3-7上下母线Vp，Vn不平衡和造成的畸变电流ia在t=0.2s加入中点平衡控制，两母线电压都稳定在400V，电网电流THD会变差。[图片] 图3-8在t=0.25s时由20%载突加至满载电流波形和母线电压波形，电压有20V左右跌落[图片] 图3-9在t=0.25s时由满载载突减至20%载电流波形和母线电压波形，电压有20V左右过冲[图片] 图3-10在t=0.25s时电网电压由220V突降至150V输入电流突然变大，母线电压由5V左右跌落[图片] 图3-11在t=0.25s时电网电压由220V突升至260V输入电流突然变小，母线电压由2V左右突升本节用PSIM搭建了系统的总体仿真模型，从理论上验证了VIENNA整流电路不但有功率因数校正功能，而且有很好的静态性能和动态性能，具有一定的实用价值。 3.4总结未来新能源充电技术将朝着大功率、高功率因数、高效率、低谐波、体积小方向发展。本文通过对Vienna整流器的分析和仿真，全面解释其工作原理和优势，限于本人水平有限，就写到这里，后续再做相关技术探讨，此文抛砖引玉，还望各位专家不吝指正，若觉得本文有可鉴之处，关注我的公众号Exdry艾昌德瑞电子科技，欢迎下载本文和相关仿真模型！[图片]

第一次发帖好像发错位置了请管理员帮忙移到综合电源讨论区噢多谢多谢！