经过我一周的学习和研究和2夜失眠,终于搞明白信号与系统中的零极点及拉普拉斯变换。其实没有想象中的复杂。学习的时候我是带着问题学习的,就是解决开关电源设计中,为了负反馈的稳定所加的补偿电容电阻是怎么计算的,为什么这样算的问题。
国内很多教材和资料讲的太高大上,学完了还是稀里糊涂的。本贴就是解决这个问题的。
经过我一周的学习和研究和2夜失眠,终于搞明白信号与系统中的零极点及拉普拉斯变换。其实没有想象中的复杂。学习的时候我是带着问题学习的,就是解决开关电源设计中,为了负反馈的稳定所加的补偿电容电阻是怎么计算的,为什么这样算的问题。
国内很多教材和资料讲的太高大上,学完了还是稀里糊涂的。本贴就是解决这个问题的。
第一章:极坐标与欧拉公式
一、极坐标
对于一个点的坐标,我们常用直角坐标系来表示。这也是我们最最常用的方式。如图1.1所示:
图1.1
对于图中的A点相当于向东走4步,再向北走3步即可到达。
然而还有一个坐标系表示法,那就是极坐标。相同的A点用极坐标表示如图1.2所示。
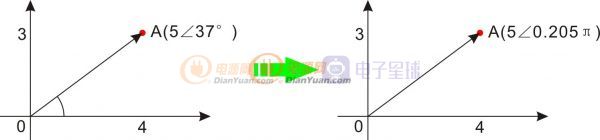
图1.2
对于图中的A点,相当于逆时针旋转37度后再走5步。然而角度的单位是度,不是数字1,对于运算来说很不方便,所以我们用弧度表示角度。你还记得吗,360度对应的弧度是2π。
直角坐标系和极坐标系虽然都能表示同一个点,但他们代表不同的模型。比如汽车的运动用直角坐标系,轮胎的运动用极坐标系。
对我们电子专业的人来说,发电机就是旋转的,所以我们用极坐标系来描述建模信号系统是最合适的。
二、欧拉公式
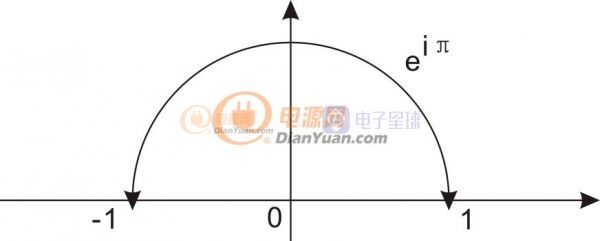
极坐标是图形,用什么公式表达呢?答案就是欧拉公式。
用图形表示就是1旋转了π度。好了,这下我们知道,以e为底的iθ就是旋转θ度。e的i2π就是转动一圈。
三、发电机的建模
我国发电机是50Hz/220V交流电,换句话说就是1秒转50圈,一圈是2π,所以这个发电机用公式表示就是e^i2π50t。通用公式就是e^i2πft。
2πf就是我们常说的角频率,通常用ω(欧米伽)表示。所以上述模型可以写成e^iωt。
又因为字母i在电路中已经表示电流了,所以电路中我们用j代替。两个字母是一个意思,所以上述模型又可以写成e^jωt。
四、发电机在复数中的表示
jω我们单独抽出来,用复数或者用复平面表示,看看应该是什么样子的,答案是下图中红点位置。这个红点就表示了这个发电机转速特性。
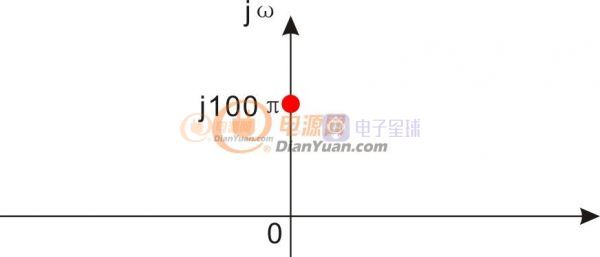
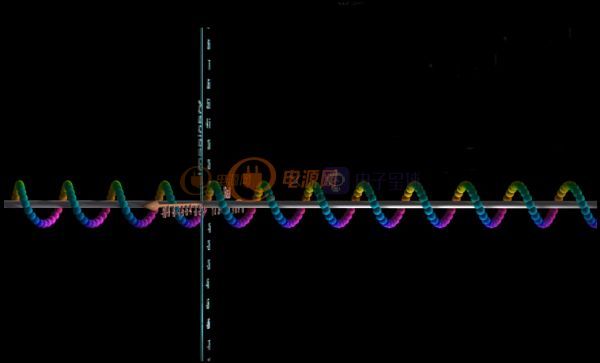
借用国外的一张视频图就是下图这个样子的波形,等幅旋转。
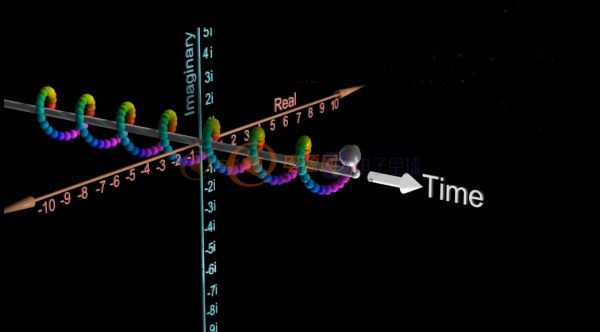
从侧面看就是我们熟悉的正弦波,等幅振荡。
好了,今天先写这么多吧,我表达清楚了吗?

