反激输出电容快速估算法

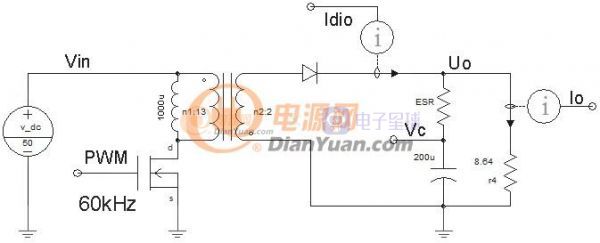
反激电路输出电容的选择方法，首先假设ESR电阻为零的情况。

                           图1-1 反激电路

按图1中的参数可以得到如下的波形曲线：

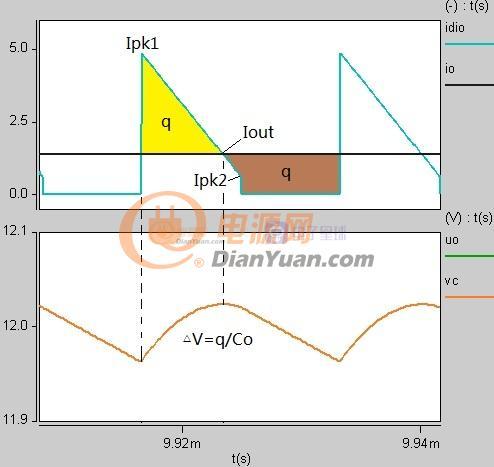
                  图1-2 深连续模式下的电流及纹波波形

图1-2中的电压纹波可以通过对输出二极管的电流积分获得，但工程应用中并不需要知道精确的波形轨迹只需求出峰值纹波即可，峰值纹波满足公式△V=q/Co所以只要求出电荷量q就能估算出纹波大小而不需要积分运算了。

图1-2中黄色q为充电棕色q为放电，稳态时二者面积相同所以无论采用哪一边的q进行计算都可以，这里显然采用右边棕色面积计算更简单q=Io*Don*T这样就得到了输出纹波电压的第一种状态表达式：

△V=q/Co=Io*Don/(Co*f)。

  当把输入电压调至70V又会获得如下波形曲线：

                       图1-3 浅连续模式的电流及纹波波形

  图1-3依然满足公式△V=q/Co，此时左侧黄色似乎更容易求解。对黄色面积求解可以有多种表达形式这里引入电流纹波率r=△I/Iavg=2*(Ipk1-Ipk2)/(Ipk1+Ipk2)，这样就得到了输出纹波电压的第二种状态：

△V=q/Co=Io*（2*Don+r）^2/(Co*f*8*r)。 

第一种状态和第二种状态的分界线为

r=2*Don

 将输入电压继续调大调制大于100V后电路进入断续模式之后纹波不在变化，此时依然按照公式△V=q/Co求解，表达式也可以有很多种这里引入峰值电流Ipk得到输出纹波电压的第三种状态：

△V=q/Co=Io*（Io+Ipk）^2/(Co*f*Ipk^2)

第二种和第三种状态的分界线为

r=2

将反激的三种状态公式汇总一下（ESR=0）

之后可以分析出一个等输出功率反激电路随着输入电压从低到高变换输出纹波的变化规律

                     图1-4 输出纹波与输入电压的关系（ESR=0）

  图中同时也给出了三种状态的分界线，可知在ESR=0的条件下深连续模式下的输出纹波最大，断续模式时纹波最小且保持不变。

 其次考虑ESR电阻不为零的情况，由于ESR电阻上产生的压降是下降的趋势而滤波电容上的电压是上升的趋势所以最后的纹波不能用估算法直接叠加而是选择其中大的一个。

浅连续或者DCM模式时

如果(Ipk1-Io)*ESR>△Vpp 则输出纹波为Ipk1*ESR，

如果(Ipk1-Io)*ESR<△Vpp 则输出纹波为Io*ESR+△Vpp

                        图1-5-1 浅连续模式

  深连续模式时

如果Ipk1*ESR>△Vpp+Ipk2*ESR 则输出纹波为Ipk1*ESR

如果Ipk1*ESR<△Vpp+Ipk2*ESR 则输出纹波为Ipk2*ESR+△Vpp

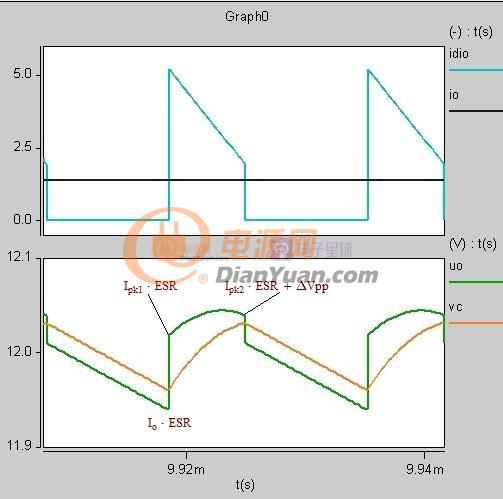
                          图1-5-2 深连续模式

  前面假设电容纹波曲线为直线（实为弧线）所以结果存在一定的误差，当ESR电阻较大峰值电流Ipk*ESR远大于电容纹波时这一误差就消除了，见下图

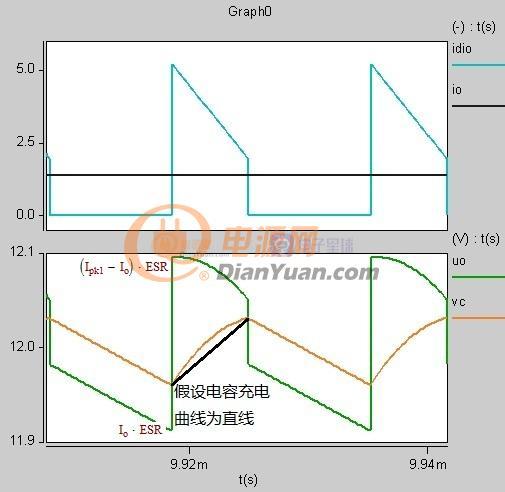
                       图1-5-3 ESR较大时的波形

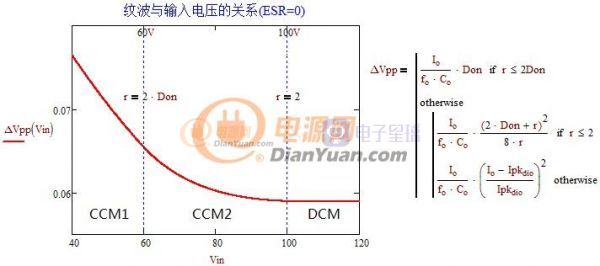
 根据上述各种情况绘制不同ESR的曲线图如下

                  图1-6 不同ESR下输出纹波与输入电压的关系

取ESR纹波=电容纹波时可以计算出临界条件以深连续模式为例（输入电压50V）根据公式

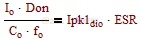
计算出ESR=0.005，设Gesr=ESR*Co可知当前条件下临界Gesr=0.1*10^-6。

对于电解电容一般Gesr=60*10^-6，根据公式可以计算出当前条件下电解电容的临界频率为2.7kHz左右，通常开关电源频率都在几十kHz以上所有如果输出采用的是电解电容可以直接用输出峰值电流乘以ESR电阻来估算（Ipk1*ESR），至此完成了反激电路最小输出电容的估算。

那要看选的电容的材质来定了。固态和普通铝电解的ESR和允许电流差异好大的，同样电压和容量。

好贴必须赞

学习了