电磁场及磁性器件
计划化一段时间把电磁场及磁性器件的知识整理一下,贴出来.但手头没有电磁场及有限元的书,希望谁能提供一下.多谢!
全部回复(10)
正序查看
倒序查看
现在还没有回复呢,说说你的想法
看到哪,想到哪,贴到那.计划先复习以下基础,麦克斯韦方程,有限元及边界条件,再给一个电感设计的仿真的实例.计算铜损;再举一个变压器的设计;计算铜损;铁损公式的获得;其他磁材料介绍.磁集成的文章思路.
矢量点积: 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149812004.gif');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149812004.gif');}" onmousewheel="return imgzoom(this);">
θ 表示两个向量之间的角度
叉积: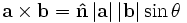 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149812210.gif');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149812210.gif');}" onmousewheel="return imgzoom(this);">
在这里 θ 表示 a 和 b 之间的角度(0° ≤ θ ≤ 180°),它位于这两个矢量所定义的平面上.而 n 是一个与 a 和 b 均垂直的单位矢量.则将右手的食指指向第一个向量的方向,右手的中指指向第二个向量的方向,那么结果向量的方向就是右手拇指的方向.
拉格朗日公式:a × (b × c) = b(a · c) − c(a · b),
梯度:标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率.
旋度:设有向量场 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817783.png');}" onmousewheel="return imgzoom(this);">,
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817783.png');}" onmousewheel="return imgzoom(this);">,
在坐标上的投影分别为 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817831.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817831.png');}" onmousewheel="return imgzoom(this);"> 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817840.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817840.png');}" onmousewheel="return imgzoom(this);"> 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817852.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817852.png');}" onmousewheel="return imgzoom(this);">
的向量叫做向量场A的旋度,记作 rot A,即
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817943.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817943.png');}" onmousewheel="return imgzoom(this);">
散度: 设有向量场 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817783.png');}" onmousewheel="return imgzoom(this);">,
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817783.png');}" onmousewheel="return imgzoom(this);">,
给出,其中P、Q、R具有一阶连续偏导数,Σ是场内的一片有向曲面,n是Σ在点(x,y,z)出的单位法向量,则 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994465.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994465.png');}" onmousewheel="return imgzoom(this);">
叫做向量场A通过曲面Σ向着制定侧的通量(或流量),而 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994492.png');}" onmousewheel="return imgzoom(this);">叫做向量场A的散度,记作 div A.
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994492.png');}" onmousewheel="return imgzoom(this);">叫做向量场A的散度,记作 div A.
高斯公式:设空间闭区域Ω是由分片光滑的闭曲面Σ所围成,函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在Ω上具有一阶连续偏导数,则有
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994819.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994819.png');}" onmousewheel="return imgzoom(this);">
或 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994852.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994852.png');}" onmousewheel="return imgzoom(this);">
这里Σ是Ω的整个边界曲面的外侧,cos α、cos β、cos γ是Σ在点(x,y,z)出的法向量的方向余弦
用散度表示 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994887.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994887.png');}" onmousewheel="return imgzoom(this);">
而 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994986.png');}" onmousewheel="return imgzoom(this);">是向量A在曲面Σ的外侧法向量上的投影
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994986.png');}" onmousewheel="return imgzoom(this);">是向量A在曲面Σ的外侧法向量上的投影
Gauss公式表达了空间闭区域上的三重积分与其边界曲面上的曲面积分之间的关系.
斯托克斯公式:设Γ为分段光滑的空间有向闭曲线,Σ是以Γ为边界的分片光滑的有向曲面,Γ的正向与Σ的侧符合右手规则,函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在曲面Σ(连同边界Γ)上具有一阶连续偏导数,则有
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149995208.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149995208.png');}" onmousewheel="return imgzoom(this);">
斯托克斯公式表达了有向曲面上的曲面积分与其边界曲线上的曲线积分之间的关系.
∇((nabla)表示向量微分算子del):梯度算符
麦克斯韦方程组:
微分形式:
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149995887.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149995887.jpg');}" onmousewheel="return imgzoom(this);">
积分形式: 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149995925.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149995925.jpg');}" onmousewheel="return imgzoom(this);">
其中,
D是电位移矢量(单位庫倫/平方米,C/m²);
B是磁通量密度(单位特斯拉,T),也称磁感强度;
E是电场强度(单位伏特/米,V/m);
H是磁场强度(单位安/米,A/m);
ρ是自由电荷体密度(单位库伦/立方米,C/m³);
J是自由电流面密度(单位安/平方米,A/m²);
磁场强度H的边界条件:nx(H2-h1)=Js 或 h2t-h1t=Js.(n x t)
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150026468.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150026468.jpg');}" onmousewheel="return imgzoom(this);">
电场强度E的边界条件:nx(E2-E1)=0. 电场强度切向分量连续
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150029521.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150029521.jpg');}" onmousewheel="return imgzoom(this);">
磁感应强度B的边界条件:n.(B2-B1)=0; 磁感应强度的法向分量连续
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150032987.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150032987.jpg');}" onmousewheel="return imgzoom(this);">
电位移D的边界条件:n.(D2-D1)=ρs; D2n-D1n=ρs
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150034048.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150034048.jpg');}" onmousewheel="return imgzoom(this);">
在各向同性的线性媒质中, 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150034225.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150034225.jpg');}" onmousewheel="return imgzoom(this);">
理想导体表面,是指σ=∞的导体,σ越大,集肤效应越显著.内部电磁场处处为零.高斯定理和安培环路定律可知,电荷和电流只能存在于理想导体的表面上.电场只有法向分量,磁场只有切向分量.
矢量点积:
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149812004.gif');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149812004.gif');}" onmousewheel="return imgzoom(this);">
θ 表示两个向量之间的角度
叉积:
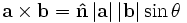 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149812210.gif');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149812210.gif');}" onmousewheel="return imgzoom(this);">
在这里 θ 表示 a 和 b 之间的角度(0° ≤ θ ≤ 180°),它位于这两个矢量所定义的平面上.而 n 是一个与 a 和 b 均垂直的单位矢量.则将右手的食指指向第一个向量的方向,右手的中指指向第二个向量的方向,那么结果向量的方向就是右手拇指的方向.
拉格朗日公式:a × (b × c) = b(a · c) − c(a · b),
梯度:标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率.
旋度:设有向量场
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817783.png');}" onmousewheel="return imgzoom(this);">,
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817783.png');}" onmousewheel="return imgzoom(this);">,
在坐标上的投影分别为
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817831.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817831.png');}" onmousewheel="return imgzoom(this);"> 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817840.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817840.png');}" onmousewheel="return imgzoom(this);"> 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817852.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817852.png');}" onmousewheel="return imgzoom(this);">
的向量叫做向量场A的旋度,记作 rot A,即
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817943.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817943.png');}" onmousewheel="return imgzoom(this);">
散度: 设有向量场
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817783.png');}" onmousewheel="return imgzoom(this);">,
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149817783.png');}" onmousewheel="return imgzoom(this);">,
给出,其中P、Q、R具有一阶连续偏导数,Σ是场内的一片有向曲面,n是Σ在点(x,y,z)出的单位法向量,则
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994465.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994465.png');}" onmousewheel="return imgzoom(this);">
叫做向量场A通过曲面Σ向着制定侧的通量(或流量),而
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994492.png');}" onmousewheel="return imgzoom(this);">叫做向量场A的散度,记作 div A.
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994492.png');}" onmousewheel="return imgzoom(this);">叫做向量场A的散度,记作 div A.
高斯公式:设空间闭区域Ω是由分片光滑的闭曲面Σ所围成,函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在Ω上具有一阶连续偏导数,则有
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994819.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994819.png');}" onmousewheel="return imgzoom(this);">
或
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994852.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994852.png');}" onmousewheel="return imgzoom(this);">
这里Σ是Ω的整个边界曲面的外侧,cos α、cos β、cos γ是Σ在点(x,y,z)出的法向量的方向余弦
用散度表示
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994887.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994887.png');}" onmousewheel="return imgzoom(this);">
而
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994986.png');}" onmousewheel="return imgzoom(this);">是向量A在曲面Σ的外侧法向量上的投影
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149994986.png');}" onmousewheel="return imgzoom(this);">是向量A在曲面Σ的外侧法向量上的投影
Gauss公式表达了空间闭区域上的三重积分与其边界曲面上的曲面积分之间的关系.
斯托克斯公式:设Γ为分段光滑的空间有向闭曲线,Σ是以Γ为边界的分片光滑的有向曲面,Γ的正向与Σ的侧符合右手规则,函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在曲面Σ(连同边界Γ)上具有一阶连续偏导数,则有
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149995208.png');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149995208.png');}" onmousewheel="return imgzoom(this);">
斯托克斯公式表达了有向曲面上的曲面积分与其边界曲线上的曲线积分之间的关系.
∇((nabla)表示向量微分算子del):梯度算符
麦克斯韦方程组:
微分形式:
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149995887.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149995887.jpg');}" onmousewheel="return imgzoom(this);">
积分形式:
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149995925.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1149995925.jpg');}" onmousewheel="return imgzoom(this);">
其中,
D是电位移矢量(单位庫倫/平方米,C/m²);
B是磁通量密度(单位特斯拉,T),也称磁感强度;
E是电场强度(单位伏特/米,V/m);
H是磁场强度(单位安/米,A/m);
ρ是自由电荷体密度(单位库伦/立方米,C/m³);
J是自由电流面密度(单位安/平方米,A/m²);
磁场强度H的边界条件:nx(H2-h1)=Js 或 h2t-h1t=Js.(n x t)
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150026468.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150026468.jpg');}" onmousewheel="return imgzoom(this);">
电场强度E的边界条件:nx(E2-E1)=0. 电场强度切向分量连续
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150029521.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150029521.jpg');}" onmousewheel="return imgzoom(this);">
磁感应强度B的边界条件:n.(B2-B1)=0; 磁感应强度的法向分量连续
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150032987.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150032987.jpg');}" onmousewheel="return imgzoom(this);">
电位移D的边界条件:n.(D2-D1)=ρs; D2n-D1n=ρs
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150034048.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150034048.jpg');}" onmousewheel="return imgzoom(this);">
在各向同性的线性媒质中,
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150034225.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/42/1150034225.jpg');}" onmousewheel="return imgzoom(this);">
理想导体表面,是指σ=∞的导体,σ越大,集肤效应越显著.内部电磁场处处为零.高斯定理和安培环路定律可知,电荷和电流只能存在于理想导体的表面上.电场只有法向分量,磁场只有切向分量.
0
回复
提示
一直没找到电磁场有限元的电子书,就简单写一下原理吧.
首先定义磁矢量A,B=∇xA.使A满足∇×H = J 和∇·B = 0.
∇·B = 0自然成立.
由∇×H = J 得∇×( 1/µ(B)(∇×A))= J
对线性同向性材料得(−1/µ)∇^2A = J
如果得到A,就可以得到B 和H.
有限元法是将求解区域剖分为多个小单元,这种小单元称为网格,一个网格内的A不变.网格的选取及疏密取决于具体场域及对精度的要求.对每个网格构造插值函数(一般用线性插值或抛物线插值)A=NiAi+NjAj+---+NnAn ,将其及对x、y的一阶偏导数代入能量方程中,将变分问题转化成能量函数W以求极值,得到节点函数的代数方程组.对于该代数问题,要用牛顿-拉斐森迭代法求解.经过适当次迭代后,右端项接近于零,从而使解趋于收敛,解得值后,通过处理即求得场量.
所以有限元法的核心是网格剖分与边界条件的确定,之后是选用现代数学进行运算求解,最后对求解结果进行分析.
下面写一下边界条件.大概有三种边界条件:
1.Dirichlet:A=0; 磁力线不穿过边界.
2.Neumann: ∂A/∂n=0; 磁力线垂直进入高到导磁体分解面.
3.Robin: ∂A/∂n+CA=0
首先定义磁矢量A,B=∇xA.使A满足∇×H = J 和∇·B = 0.
∇·B = 0自然成立.
由∇×H = J 得∇×( 1/µ(B)(∇×A))= J
对线性同向性材料得(−1/µ)∇^2A = J
如果得到A,就可以得到B 和H.
有限元法是将求解区域剖分为多个小单元,这种小单元称为网格,一个网格内的A不变.网格的选取及疏密取决于具体场域及对精度的要求.对每个网格构造插值函数(一般用线性插值或抛物线插值)A=NiAi+NjAj+---+NnAn ,将其及对x、y的一阶偏导数代入能量方程中,将变分问题转化成能量函数W以求极值,得到节点函数的代数方程组.对于该代数问题,要用牛顿-拉斐森迭代法求解.经过适当次迭代后,右端项接近于零,从而使解趋于收敛,解得值后,通过处理即求得场量.
所以有限元法的核心是网格剖分与边界条件的确定,之后是选用现代数学进行运算求解,最后对求解结果进行分析.
下面写一下边界条件.大概有三种边界条件:
1.Dirichlet:A=0; 磁力线不穿过边界.
2.Neumann: ∂A/∂n=0; 磁力线垂直进入高到导磁体分解面.
3.Robin: ∂A/∂n+CA=0
0
回复
提示
@feelbetter
一直没找到电磁场有限元的电子书,就简单写一下原理吧.首先定义磁矢量A,B=∇xA.使A满足∇×H=J和∇·B=0.∇·B=0自然成立.由∇×H=J得∇×(1/µ(B)(∇×A))=J对线性同向性材料得(−1/µ)∇^2A=J如果得到A,就可以得到B和H.有限元法是将求解区域剖分为多个小单元,这种小单元称为网格,一个网格内的A不变.网格的选取及疏密取决于具体场域及对精度的要求.对每个网格构造插值函数(一般用线性插值或抛物线插值)A=NiAi+NjAj+---+NnAn,将其及对x、y的一阶偏导数代入能量方程中,将变分问题转化成能量函数W以求极值,得到节点函数的代数方程组.对于该代数问题,要用牛顿-拉斐森迭代法求解.经过适当次迭代后,右端项接近于零,从而使解趋于收敛,解得值后,通过处理即求得场量.所以有限元法的核心是网格剖分与边界条件的确定,之后是选用现代数学进行运算求解,最后对求解结果进行分析.下面写一下边界条件.大概有三种边界条件:1.Dirichlet:A=0;磁力线不穿过边界.2.Neumann:∂A/∂n=0;磁力线垂直进入高到导磁体分解面.3.Robin:∂A/∂n+CA=0
好东西!
0
回复
提示
电感和变压器的设计例子用FEMM, 虽然界面很不好,但这是一个真正free的软件.仿真的结果不影响对问题的理解.对于开关电源的铜损,要针对电流的波形傅利叶分析,得到各次谐波.用不同的频率,分别仿真,在线性叠加.这一点不如Ansoft等软件.但即使是Ansoft等很贵的软件,对于新形状的变压器,也需要售后服务.举一个带气隙电感小例子;结果如下: .如果感兴趣,可以改变变压器尺寸,频率,绕组的位置,串并联,同轴绕,观察结果.能得到一些有用的结论:靠近气隙部分的损耗明显加剧了损耗;并联的绕组由于临近效应使电流不平均分配.好好利用这些能明显的降低损耗.仿真步骤:画图-〉定义铜,铁心,空气等材料-〉定义绕组峰值电流及串并联-〉定义边界条件-〉生成网格-〉运行计算得到结果根据结果,可以得到磁感应强度及电流密度的分布,得到损耗,电感量等.Ansoft等软件不需要将波形付利叶分解.而femm只运行点一频率.需要将电流波形分解.http://en.wikipedia.org/wiki/Fourier_series功率的k次谐波分量为(ak^2+bk^2)/2;电流有效值的k次谐波分量为((ak^2+bk^2)/2)^(0.5)
.如果感兴趣,可以改变变压器尺寸,频率,绕组的位置,串并联,同轴绕,观察结果.能得到一些有用的结论:靠近气隙部分的损耗明显加剧了损耗;并联的绕组由于临近效应使电流不平均分配.好好利用这些能明显的降低损耗.仿真步骤:画图-〉定义铜,铁心,空气等材料-〉定义绕组峰值电流及串并联-〉定义边界条件-〉生成网格-〉运行计算得到结果根据结果,可以得到磁感应强度及电流密度的分布,得到损耗,电感量等.Ansoft等软件不需要将波形付利叶分解.而femm只运行点一频率.需要将电流波形分解.http://en.wikipedia.org/wiki/Fourier_series功率的k次谐波分量为(ak^2+bk^2)/2;电流有效值的k次谐波分量为((ak^2+bk^2)/2)^(0.5)
 .如果感兴趣,可以改变变压器尺寸,频率,绕组的位置,串并联,同轴绕,观察结果.能得到一些有用的结论:靠近气隙部分的损耗明显加剧了损耗;并联的绕组由于临近效应使电流不平均分配.好好利用这些能明显的降低损耗.仿真步骤:画图-〉定义铜,铁心,空气等材料-〉定义绕组峰值电流及串并联-〉定义边界条件-〉生成网格-〉运行计算得到结果根据结果,可以得到磁感应强度及电流密度的分布,得到损耗,电感量等.Ansoft等软件不需要将波形付利叶分解.而femm只运行点一频率.需要将电流波形分解.http://en.wikipedia.org/wiki/Fourier_series功率的k次谐波分量为(ak^2+bk^2)/2;电流有效值的k次谐波分量为((ak^2+bk^2)/2)^(0.5)
.如果感兴趣,可以改变变压器尺寸,频率,绕组的位置,串并联,同轴绕,观察结果.能得到一些有用的结论:靠近气隙部分的损耗明显加剧了损耗;并联的绕组由于临近效应使电流不平均分配.好好利用这些能明显的降低损耗.仿真步骤:画图-〉定义铜,铁心,空气等材料-〉定义绕组峰值电流及串并联-〉定义边界条件-〉生成网格-〉运行计算得到结果根据结果,可以得到磁感应强度及电流密度的分布,得到损耗,电感量等.Ansoft等软件不需要将波形付利叶分解.而femm只运行点一频率.需要将电流波形分解.http://en.wikipedia.org/wiki/Fourier_series功率的k次谐波分量为(ak^2+bk^2)/2;电流有效值的k次谐波分量为((ak^2+bk^2)/2)^(0.5) 0
回复
提示
读了一些平面变压器的文章,平面变压器在DC/DC模块已经应用的十分普遍,也逐渐在AC/DC中应用,顺便整理一下:
1.共模电容问题.
1150686438.pdf
http://bbs.dianyuan.com/topic/6397
http://bbs.dianyuan.com/topic/48229
2. 在同层多绕组,绕组的线宽的优化: 使每一匝的电阻相等,求得优化系数k=R外/R内
3. 根据Foundementals of Powar Electronics中变压器部分中临近效应的描述,适当安排绕组.觉得还是用有限元的软件简单一些.
4. 根据经验公式计算磁损.
1.共模电容问题.
1150686438.pdf
http://bbs.dianyuan.com/topic/6397
http://bbs.dianyuan.com/topic/48229
2. 在同层多绕组,绕组的线宽的优化: 使每一匝的电阻相等,求得优化系数k=R外/R内
3. 根据Foundementals of Powar Electronics中变压器部分中临近效应的描述,适当安排绕组.觉得还是用有限元的软件简单一些.
4. 根据经验公式计算磁损.
0
回复
提示
磁材料损耗功率(P)由磁滞损耗(Ph)、涡流损耗(Pe)和剩余损耗(Pc)组成:Pc=Ph+Pe+Pc
磁滞损耗正比于磁滞回线面积和工作频率.
涡流一方面产生磁芯损耗,另一方面产生集肤效应.
剩余损耗是一个人为定义的量.如图:
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/43/1152578504.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/43/1152578504.jpg');}" onmousewheel="return imgzoom(this);">
计算铁损以前是一个比较困难的题目,通常的根据经验公式计算,常见的公式为:Pr=k*(f^a)*(B^b)*V
现在如mathcad等计算软件,对曲线的拟和把工作大大简化.
还有一个问题是在仿真有磁性材料的电路时,对于磁性材料非线性的处理,见过有效的软件处理这个问题,得到和实测一致的结果.
磁滞损耗正比于磁滞回线面积和工作频率.
涡流一方面产生磁芯损耗,另一方面产生集肤效应.
剩余损耗是一个人为定义的量.如图:
 500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/43/1152578504.jpg');}" onmousewheel="return imgzoom(this);">
500) {this.resized=true; this.width=500; this.alt='这是一张缩略图,点击可放大。\n按住CTRL,滚动鼠标滚轮可自由缩放';this.style.cursor='hand'}" onclick="if(!this.resized) {return true;} else {window.open('http://u.dianyuan.com/bbs/u/43/1152578504.jpg');}" onmousewheel="return imgzoom(this);">
计算铁损以前是一个比较困难的题目,通常的根据经验公式计算,常见的公式为:Pr=k*(f^a)*(B^b)*V
现在如mathcad等计算软件,对曲线的拟和把工作大大简化.
还有一个问题是在仿真有磁性材料的电路时,对于磁性材料非线性的处理,见过有效的软件处理这个问题,得到和实测一致的结果.
0
回复
提示
@feelbetter
下面对磁集成进行一些研究.发现一篇陈乾宏的资料,也许有帮助,打算由此入手.1152674183.ppt
Gordon Bloom 根据电路的电压与磁通的关系,给出了IM的推导.并应用移源原理得到低漏感等变换.移源原理在倍流电路的变换也得到好的效果.
陈乾宏论文中提到两种得到磁集成方法,1共用变压器及电感低磁阻通路.2没有共用的低磁阻通路,但各绕组解耦不互相干扰的前提下得到叠加变换.在得到磁集成的变压器后,通过用加入低磁阻通路等解耦的办法,得到分立的磁性器件模型,得到一些新的等价拓扑.磁集成的变压器根据对耦等价变换可以得到相应的电路模型,与原变换前的模型比较,由于变换的基础是电压等效,所以支路电压保持不变,如果变换中使支路耦合,则得到电路电流的差异.
Volterra专利的多路耦合电感在多相buck电路,可以考虑成磁集成,相数多,磁通抵消得多.
陈乾宏论文中提到两种得到磁集成方法,1共用变压器及电感低磁阻通路.2没有共用的低磁阻通路,但各绕组解耦不互相干扰的前提下得到叠加变换.在得到磁集成的变压器后,通过用加入低磁阻通路等解耦的办法,得到分立的磁性器件模型,得到一些新的等价拓扑.磁集成的变压器根据对耦等价变换可以得到相应的电路模型,与原变换前的模型比较,由于变换的基础是电压等效,所以支路电压保持不变,如果变换中使支路耦合,则得到电路电流的差异.
Volterra专利的多路耦合电感在多相buck电路,可以考虑成磁集成,相数多,磁通抵消得多.
0
回复
提示

