之前讲过正弦电路的分析。正弦电路的分析就是交流电路的分析。交流电路时随着时间变化的,分析起来不像直流电路那么简单。所以采用向量法,将一个随时间变化的量,用向量的形式表达。

可以看到,含有电感和电容的交流电路的阻抗是随着频率变化的。因此系统的阻抗是随着频率变化的。这一章主要根据之前讲过的电阻,电感,电容的相量表示来分析交流电路。主要分析在不同频率下电路的特性及其应用。
串联电路的谐振
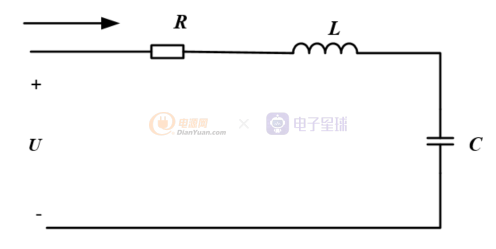
根据电路图,可列阻抗特性公式如下:
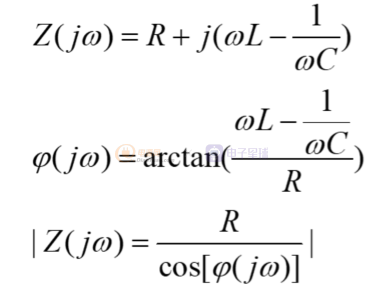
当阻抗的阻抗角为0时,此时电感阻抗和电容阻抗相互抵抗完全抵消:
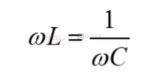
此时,电压和电流同相位。此状态被成为谐振状态。RLC串联电路的谐振状态的阻抗最小。并不是每个电路的谐振状态的谐振阻抗都是最小的。
注:谐振状态是通过阻抗角来判断的。
交流电路的分析就是将电感感抗和电容容抗用频率的表示。然后分析每个部分的电压和电流。上面简单讲述了RLC串联电路的分析方法。其他电路分析方法不变,将不再重复。
下面介绍交流电路频率响应的应用。
还是上面RLC电路
输入电压为U
电路阻抗为

先定性分析,电阻两端分压是不会根据频率的改变而改变的。电感两端的分压随着频率的增加而增加,电容两端的分压随着频率的增加而降低。在频率很低,电容两端电压较大,电感两点电压较小,频率很高,电容两端电压很低,电感两端电压很高,若以电容电压作为输出,则可以达到低通滤波的效果。若以电感电压作为输出,则可以达到高通滤波的效果。
定量分析如下:
则电容、电感、电阻电压如下:
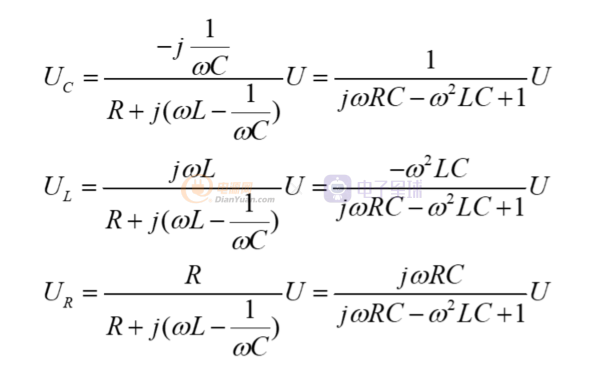
当w很小时

当w很大时

频率很小时,电容电压很大,频率很大时,电感电压很大。与上述分析一致。
本章简单介绍交流电路的频率响应和及有关滤波器的基础知识,有关滤波器的详细介绍后续将有专门专题讲解。


