近日笔者在阅读Shift-GCN[2]的文献，Shift-GCN是在传统的GCN的基础上，用Shift卷积算子[1]取代传统卷积算子而诞生出来的，可以用更少的参数量和计算量达到更好的模型性能，笔者感觉蛮有意思的，特在此笔记。本文转载自徐飞翔的“Shift-GCN网络论文笔记”

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

Shift-GCN是用于骨骼点序列动作识别的网络，为了讲明其提出的背景，有必要先对ST-GCN网络进行一定的了解。

ST-GCN网络

骨骼点序列数据是一种天然的时空图结构数据，具体分析可见[5,6]，针对于这类型的数据，可以用时空图卷积进行建模，如ST-GCN[4]模型就是一个很好的代表。简单来说，ST-GCN是在空间域上采用图卷积的方式建模，时间域上用一维卷积进行建模。

骨骼点序列可以形式化表达为一个时空图，其中有着个关节点和帧。骨骼点序列的输入可以表达为 $\mathbf{X} \in \mathbb{R}^{N \times T \times d}$ ，其中表示维度。为了表示人体关节点之间的连接，我们用邻接矩阵表达。按照ST-GCN原论文的策略，将人体的邻接矩阵划分为三大部分：1）离心群；2）向心群；3）根节点。具体的细节请参考论文[4]。每个部分都对应着其特定的邻接矩阵 $\mathbf{A}_p$ , $p\in\mathcal{P}$ 其中表示划分部分的索引。用符号 $\mathbf{F} \in \mathbb{R}^{N \times C}$ 和 $′ \mathbf{F}^{\prime} \in \mathbb{R}^{N \times C^{\prime}}$ 分别表示输入和输出的特征矩阵，其中和 $C^{\prime}$ 是输入输出的通道维度。那么，根据我们之前在GCN系列博文[7,8,9]中介绍过的，我们有最终的人体三大划分的特征融合为：

$′ \mathbf{F}^{\prime} =\sum_{p\in\mathcal{P}}\bar{A}_{p}FW_{p}(1.1)$

其中P = { 根节点，离心群，向心群 } ， $\bar{\mathbf{A}}_p = \Lambda_p^{-\frac{1}{2}} \mathbf{A}_p \Lambda_p^{-\frac{1}{2}} \in \mathbb{R}^{N \times N}$ 是标准化后的邻接矩阵，其中 $\Lambda_p^{ii} = \sum_j(\mathbf{A}_p^{ij})+\alpha$ ，具体这些公式的推导，见[7,8,9]。其中的 $\mathbf{W}_p \in \mathbb{R}^{1 \times 1 \times C \times C^{\prime}}$ 是每个人体划分部分的1x1卷积核的参数，需要算法学习得出。整个过程如Fig 1.1所示。

Fig 1.1 STGCN的示意图，通过不同的邻接矩阵可以指定不同的身体划分部分，通过1x1卷积可以融合通道间的信息，最后融合不同划分部分的信息就形成了新的输出向量。

ST-GCN的缺点体现在几方面：

计算量大，对于一个样本而言，ST-GCN的计算量在16.2GFLOPs，其中包括4.0GFLOPs的空间域图卷积操作和12.2GFLOPs的时间一维卷积操作。
ST-GCN的空间和时间感知野都是固定而且需要人为预先设置的，有些工作尝试采用可以由网络学习的邻接矩阵的图神经网络去进行建模[10,11]，即便如此，网络的表达能力还是受到了传统的GCN的结构限制。

Shift-GCN针对这两个缺点进行了改进。

Shift-GCN

这一章对Shift-GCN进行介绍，Shift-GCN对ST-GCN的改进体现在对于空间信息（也就是单帧的信息）的图卷积改进，以及时序建模手段的改进（之前的工作是采用一维卷积进行建模的）。

Spatial Shift-GCN

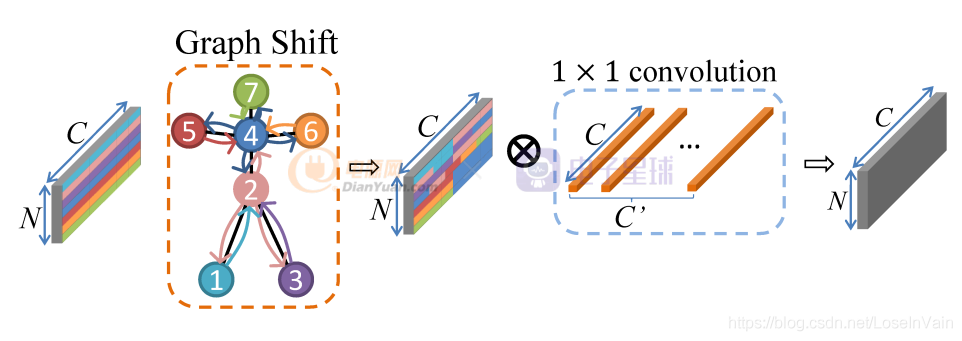
Shift-GCN是对ST-GCN的改进，其启发自Shift卷积算子[1]，主要想法是利用1x1卷积算子结合空间shift操作，使得1x1卷积同时可融合空间域和通道域的信息，具体关于shift卷积算子的介绍见博文[12]，此处不再赘述，采用shift卷积可以大幅度地减少参数量和计算量。如Fig 2.1所示，对于单帧而言，类似于传统的Shift操作，可以分为Graph Shift和1x1 conv两个阶段。然而，和传统Shift操作不同的是，之前Shift应用在图片数据上，这种数据是典型的欧几里德结构数据[7]，数据节点的邻居节点可以很容易定义出来，因此卷积操作也很容易定义。而图数据的特点决定了其某个数据节点的邻居数量（也即是“度”）都可能不同，因此传统的卷积在图数据上并不管用，传统的shift卷积操作也同样并不能直接在骨骼点数据上应用。那么就需要重新在骨骼点数据上定义shift卷积操作。

作者在[2]中提出了两种类型的骨骼点Shift卷积操作，分别是：

局部Shift图卷积（Local Shift Graph Convolution）
全局Shift图卷积（Global Shift Graph Convolution）

下文进行简单介绍。

Fig 2.1 采用了shift卷积算子的GCN，因为骨骼点序列属于图数据，因此需要用特别的手段去定义shift操作。

局部shift图卷积

在局部shift图卷积中，依然只是考虑了骨骼点的固有物理连接，这种连接关系与不同数据集的定义有关，具体示例可见博文[13]，显然这并不是最优的，因为很可能某些动作会存在节点之间的“超距”关系，举个例子，“拍掌”和“看书”这两个动作更多取决于双手的距离之间的变化关系，而双手在物理连接上并没有直接相连。

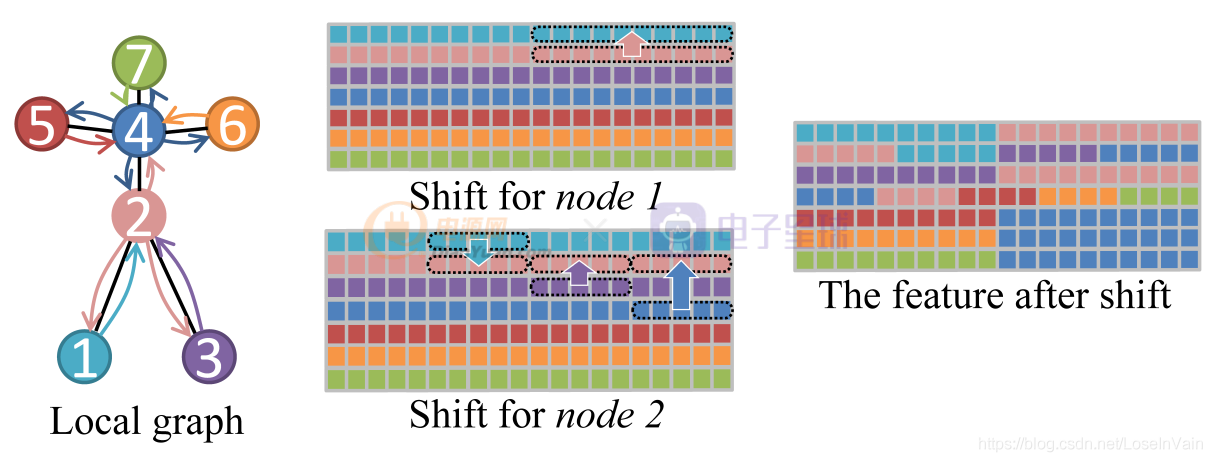
尽管局部shift图卷积只考虑骨骼点的固有连接，但是作为一个好的基线，也是一个很好的尝试，我们开始讨论如何定义局部shift图卷积。如Fig 2.2所示，为了简便，我们假设一个骨架的骨骼点只有7个，连接方式如图所示，不同颜色代表不同的节点。对于其中某个节点 , $v\in[1,7]v$ 而言，用 $B_v = \{B_v^1,B_v^2,\cdots,B_v^n\}$ 表示节点v vv的邻居节点，其中是邻居节点的数量。类似于传统的Shift卷积中所做的，对于每一个节点的特征向量 $\mathbf{F}_v \in \mathbb{R}^{C}$ ，其中是通道的数量，我们将通道均匀划分为份片区，也即是每一份片区包含有 $c = \lfloor \dfrac{C}{n+1} \rfloor$ 个通道。我们让第一份片区保留本节点（也即是节点本身）的特征，而剩下的个片区分别从邻居 $B_v^1,B_v^2 ,\cdots,B_v^n$ 中通过平移（shift）操作得到，如式子(2.1)所示。用 $\mathbf{F} \in \mathbb{R}^{N \times C}$ 表示单帧的特征，用 $\widetilde{\mathbf{F}} \in \mathbb{R}^{N \times C}$ 表示图数据shift操作之后的对应特征，其中表示节点的数量，表示特征的维度，本例子中。

$\tilde{F}_{v}=F_{(v,0:c)}||F_{(B_{v}^{1},:2c)}||F_{(B_{v}^{2},2c:3c)}||\cdots|||F_{(B_{v}^{n},nc:)}(2.1)$

整个例子的示意图如Fig 2.2所示，其中不同颜色的节点和方块代表了不同的节点和对应的特征。以节点1和节点2的shift操作为例子，节点1的邻居只有节点2，因此把节点1的特征向量均匀划分为2个片区，第一个片区保持其本身的特征，而片区2则是从其对应的邻居，节点2中的特征中平移过去，如Fig 2.2的Shift for node 1所示。类似的，以节点2为例子，节点2的邻居有节点4，节点1，节点3，因此把特征向量均匀划分为4个片区，同样第一个片区保持其本身的特征，其他邻居节点按照序号升序排列，片区2则由排列后的第一个节点，也就是节点1的特征平移得到。类似的，片区3和片区4分别由节点3和节点4的对应片区特征平移得到。如Fig 2.2的Shift for node 2所示。最终对所有的节点都进行如下操作后，我们有 $\widetilde{\mathbf{F}}$ 如Fig 2.2的The feature after shift所示。

Fig 2.2 局部shift图卷积操作的示意图，假设骨骼点数据只有7个骨骼点节点。

全局shift图卷积

局部shift图卷积操作有两个缺点：

只考虑物理固有连接，难以挖掘潜在的“超距”作用的关系。
数据有可能不能被完全被利用，如Fig 2.2的节点3的特征为例子，如Fig 2.3所示，节点3的信息在某些通道遗失了，这是因为不同节点的邻居数量不同。

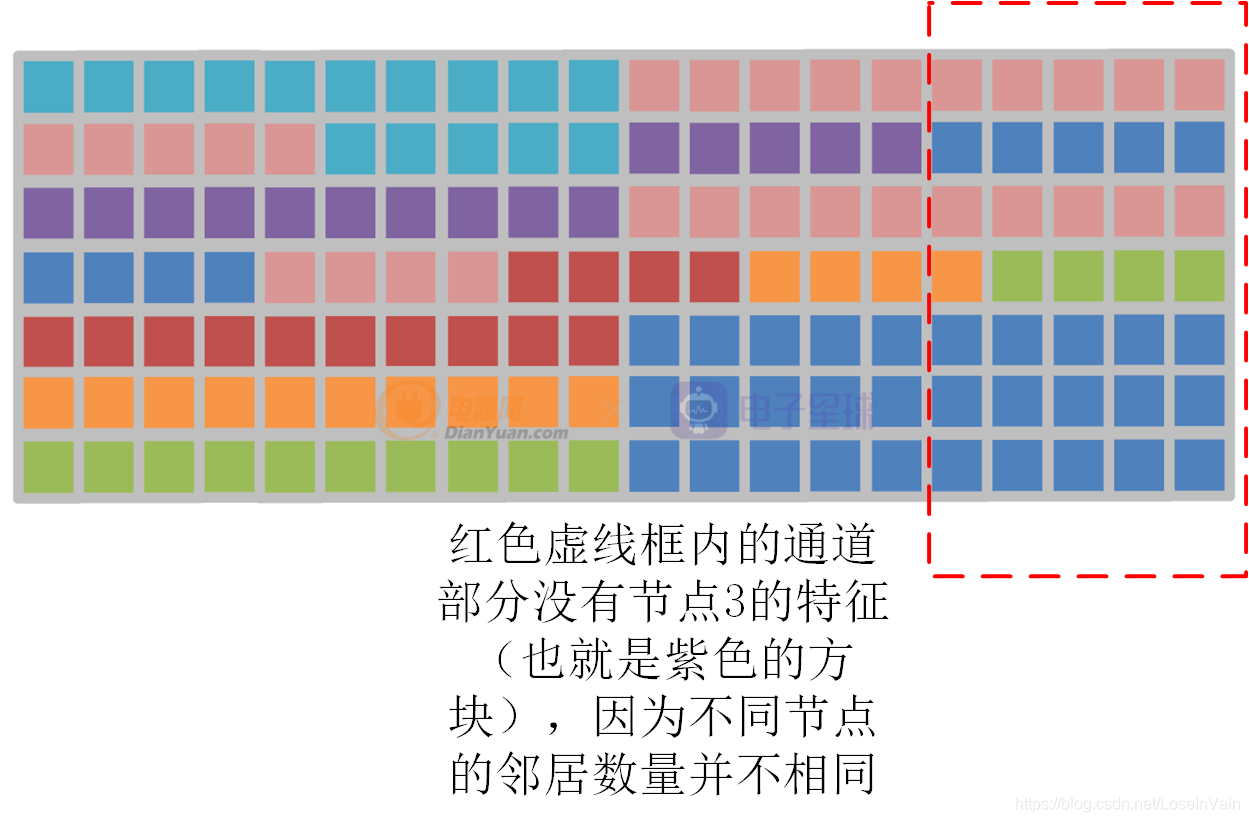
Fig 2.3 红色虚线框内的通道部分完全失去了节点3的特征信息（也即是紫色方块）。

为了解决这些问题，作者提出了全局Shift图卷积，如Fig 2.4所示。其改进很简单，就是去除掉物理固有连接的限制，将单帧的骨骼图变成完全图，因此每个节点都会和其他任意节点之间存在直接关联。给定特征图 $\mathbf{F} \in \mathbb{R}^{N \times C}$ ，对于第i ii个通道的平移距离 $d = i \bmod N$ 。这样会形成类似于螺旋状的特征结构，如Fig 2.4的The feature after shift所示。

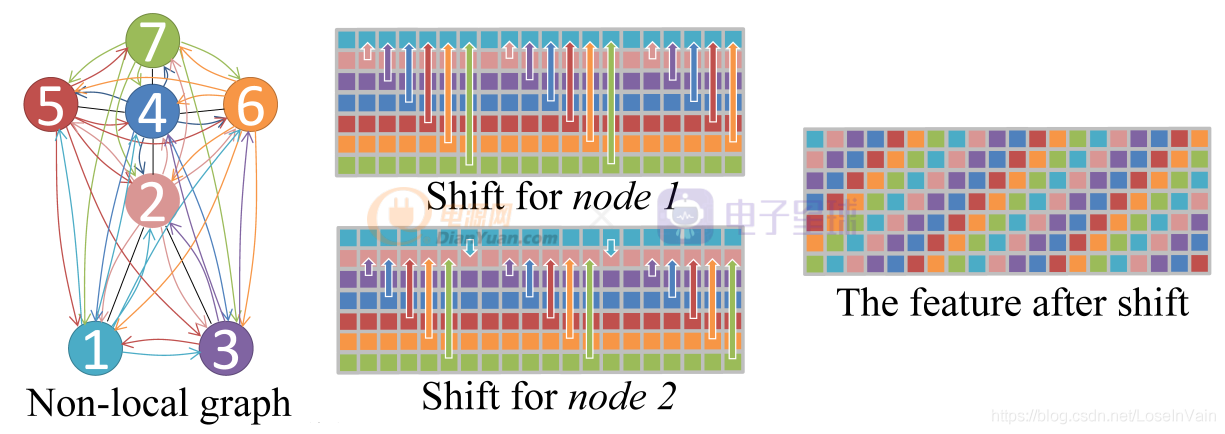
Fig 2.4 全局shift图卷积操作的示意图，假设骨骼点数据只有7个骨骼点节点。其中和局部shift图卷积操作的区别在于，当前的图是完全图，也即是完全连接的图了。

为了挖掘骨骼完全图中的人体关键信息，把重要的连接给提取出来，作者在全局shift图卷积基础上还使用了注意力机制，如式子(2.2)所示。

$\tilde{F}_{M}=\tilde{F}\circ(tanh(M)+1)(2.2)$

Temporal Shift-GCN

在空间域上的shift图卷积定义已经讨论过了，接下来讨论在时间域上的shift图卷积定义。如Fig 2.5所示，考虑到了时序之后的特征图层叠结果，用符号 $\mathbf{F} \in \mathbb{R}^{T \times N \times C}$ 表示时空特征图，其中有 $\mathbf{F} = \{\mathbf{F}^1,\mathbf{F}^2,\cdots,\mathbf{F}^{T}\}$ 。这种特征图可以天然地使用传统的Shift卷积算子，具体过程见[12]，我们称之为naive temporal shift graph convolution。在这种策略中，我们需要将通道均匀划分为个片区，每个片区有着偏移量为 $-u,-u+1,\cdots,0,\cdots,u-1,u$ 。与[12]策略一样，移出去的通道就被舍弃了，用0去填充空白的通道。这种策略需要指定u uu的大小，涉及到了人工的设计，因此作者提出了adaptive temporal shift graph convolution，是一种自适应的时序shift图卷积，其对于每个通道，都需要学习出一个可学习的时间偏移参数 $S_i,i=1,2,\cdots,C$ 。如果该参数是整数，那么无法传递梯度，因此需要放松整数限制，将其放宽到实数，利用线性插值的方式进行插值计算，如式子(2.3)所示。

$\tilde{F}_{(v,t,i)}=(1-\lambda)⋅F_{(v, \lfloor t+S_{i} \rfloor,i)}+\lambda⋅F_{(v, \lfloor t+S_{i}\rfloor +1 ,i)}(2.3)$

其中 $\lambda = S_i - \lfloor S_i\rfloor$ 是由于将整数实数化之后产生的余量，需要用插值的手段进行弥补，由于实数化后，锚点落在了 $[\lfloor t+S_i\rfloor, \lfloor t+S_i\rfloor+1]$ 之间，因此在这个区间之间进行插值。

Fig 2.5 考虑到时序后的特征图层叠结果。

网络

结合spatial shift-gcn和temporal shift-gcn操作后，其网络基本单元类似于ST-GCN的设计，如Fig 2.6所示。

Fig 2.6 Shift-Conv模块和Shift-Conv-Shift模块的设计都是参考了ST-GCN和传统Shift卷积网络设计的。

Update 20201130:来自一个知乎朋友的问题：

ID:fightingQ:好巧啊，又跟你看到同一篇论文了。不知道还记得我吗。这里的naive temporal shift 写的不详细。不知道我理解的对不对，想跟你探讨一下。对于每一个节点的c个通道，划分为u个部分。每个部分分别替换为其第-u，，，0,1，u帧处的对应特征，其中0指的是节点本身的这一部分特征。这样每一个节点就会包含了2u+1帧的信息。在adaptive中，每个通道都设置了一个可学习的移动参数，但是这个移动参数是怎么来学的。我随意设置这样一个学习的shift参数，学习的依据是啥呢？

回答：正如原文所讲的，其中的naive temporal shift完全是按照传统的shift卷积算子操作进行计算的，具体见[1]。我们知道，进行通道上的shift操作的目的在于改变卷积的感知野，因此文中提到的超参数其实就是控制了每一层的时序感知野大小，但是这样有几个缺点：

卷积是具有层次结构的，每一层的u uu如果都一样，那么感知野理论上也是一样的，这样不合理，因此卷积的层次结构意味着感知野大小不一定一致。
需要人工去设置这个超参数，对于不同数据集的结果都不一样，工作量大。

因此，引入了所谓的自适应时序 shift，其出发点就是通过反向梯度传播去学习每一层的感知野，也就是每一层都有一个，因为需要确保可以求导，这个参数必须是保证为浮点数才能存在梯度，因此shift操作被泛化到插值操作，正如式子(2.3)所示。

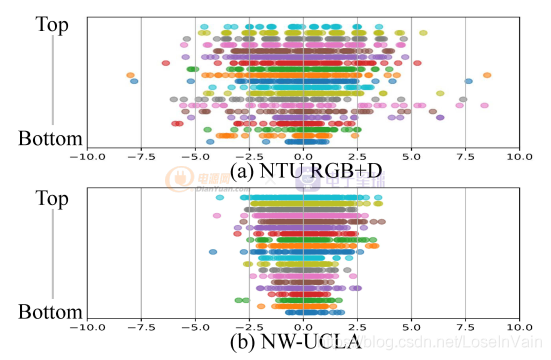
其实原论文对这个自适应学习出来的参数进行了可视化，如Fig a1所示，作者对于不同的数据集（NTU RGBD和NW-UCLA）上进行了adaptive temporal shift的每一层的结果的可视化（具体分析见原论文），简单来说，顶层（top layer，也即是输出层）的值范围都比较大（表现为值的范围比较宽广），意味着输出层需要的时序感知野比较大，这一点很容易理解，因为输出层需要更多的时序语义信息，因此感知野比较大是正常的；而底层（bottom layer，也即是输入层）的值范围都比较小，这一点也很好理解，输入层更多的是单帧的底层信息建模（比如纹理，色彩，边缘信息等），因此时序感知野比较小是正常的。

通过这种自适应的学习手段，确保了对不同层的shift系数的独立学习，因此使得不同层具有不同的时序感知野。

以上。

Fig a1. 对不同数据集上学习到的时序平移系数进行可视化的结果，(a)为NTU RGBD数据集结果，(b)为NW-UCLA数据集的结果。我们发现底层（输入层）的值都偏小，顶层（输出层）的值偏大。意味着输入层的感知野需求比较小，而输出层的感知野需求比较大。

Reference

[1]. Wu, B., Wan, A., Yue, X., Jin, P., Zhao, S., Golmant, N., … & Keutzer, K. (2018). Shift: A zero flop, zero parameter alternative to spatial convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 9127-9135).

[2]. Cheng, K., Zhang, Y., He, X., Chen, W., Cheng, J., & Lu, H. (2020). Skeleton-Based Action Recognition With Shift Graph Convolutional Network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 183-192).

[3]. https://fesian.blog.csdn.net/article/details/109474701

[4]. Sijie Yan, Yuanjun Xiong, and Dahua Lin. Spatial temporal graph convolutional networks for skeleton-based action recognition. In Thirty-Second AAAI Conference on Artificial Intelligence, 2018.

[5]. https://fesian.blog.csdn.net/article/details/105545703

[6]. https://blog.csdn.net/LoseInVain/article/details/87901764

[7]. https://blog.csdn.net/LoseInVain/article/details/88373506

[8]. https://fesian.blog.csdn.net/article/details/90171863

[9]. https://fesian.blog.csdn.net/article/details/90348807

[10]. Lei Shi, Yifan Zhang, Jian Cheng, and Hanqing Lu. Skeleton-based action recognition with directed graph neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 7912–7921, 2019

[11]. Lei Shi, Yifan Zhang, Jian Cheng, and Hanqing Lu. Two stream adaptive graph convolutional networks for skeleton based action recognition. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 2019.

[12]. https://fesian.blog.csdn.net/article/details/109474701

[13]. https://fesian.blog.csdn.net/article/details/108242717