前面我们讨论了BUCK变换器的工作模式,通过仿真波形分析了过程以及计算方法,那么本文将从前面所仿真的波形变化提取出相关的器件选型计算。
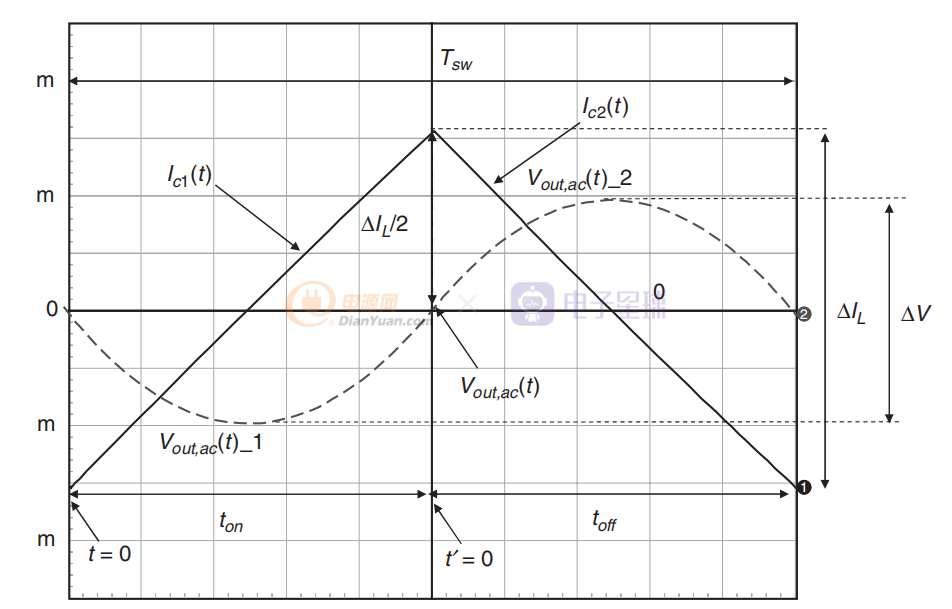
上图显示了流经输出电容器的线性上升和下降电流。 从前面方程,我们知道电容器两端的电压,在我们的应用中为 Vout,是通过对电容器电流 IC(t) 进行积分获得的。 电流是一个斜坡,由形式为ax的简单直线方程描述。 因此,它的积分看起来像抛物线表达式,满足形式 。 由于信号是不连续的,我们需要将其限制在已知限制之间。 第一个将介于 0 和 ton (IC1) 之间,而第二个 IC2 可能介于 ton 和 Tsw 之间。 但是,为了简化分析,我们将 IC2 绑定在 0 和 toff 之间。
请注意,我们只关心 Vout 的交流部分(实际纹波),因此符号 Vout,ac(t) 是 Vout(t) 减去其直流部分。
我们先表达IC1和IC2的电容电流表达式:
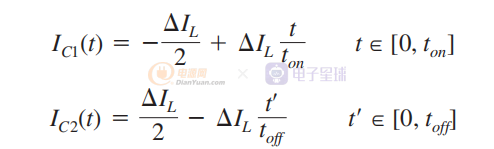
实际上是总电流纹波的二分之一。 为了获得输出纹波的图像, 通过从 0 到 t 对 IC1 和 IC2 进行积分。

由于我们对上述函数的幅度感兴趣,我们知道峰值会影响它们。 通过将它们各自的导数项归零 ,我们将找到这些函数达到峰值的确切时刻:

现在可以通过减去方程得出总峰峰值纹波 δV:
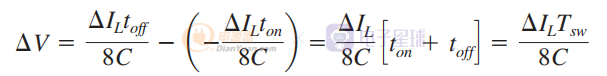
该等式描述了 CCM 降压转换器的峰峰值纹波定义,可用于计算与所需纹波相关的输出电容器。 请注意,此定义不包括等效串联电阻 (ESR) 效应。
现在的练习在于计算降压转换器的δIL, 从图中,在平衡时,电流从-δIL/2开始,上升到+δIL/2 ,然后又回到-δIL/2 。 因此可以从这个表达式导出一个简单的等式:

联立上述等式可以得到δIL:

可以得到最终的δV:
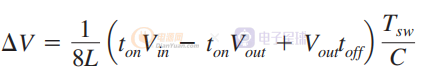
我们知道ton=DTsw,toff=(1-D)Tsw,那么进一步可以得到:

由于我们将降压转换器视为一个方波发生器,后跟一个 LC 滤波器,因此我们知道这种滤波器的截止频率为:
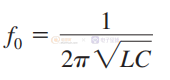
可以得到:
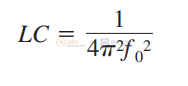
替换方程中的 LC,并引入 Fsw、开关频率、可得:
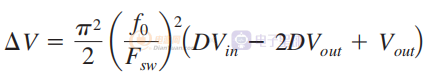
为了简化这个表达式,可以将纹波归一化为输出电压 Vout。 等式因此可以更新为
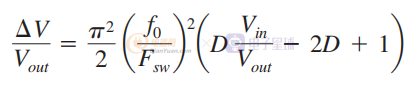
已知D=Vout/Vin,我们可以得到:
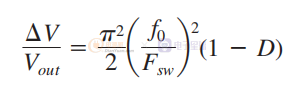

ESR 看起来像一个与电容器串联的电阻器。 交流电感电流纹波不再单独穿过 C,而是 C 加上串联 RESR 的电阻的组合。 实际上,等效电感也存在,但在这种情况下我们将忽略它。
可以得到一个很简单的等式:
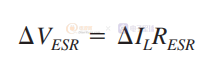
我们知道电感纹波电流流入RESR。 所以,
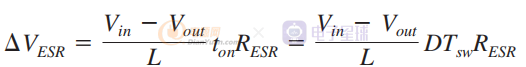
已知D=Vout/Vin,分子分母同时除以Vout:
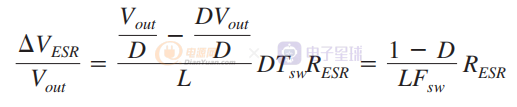
根据电容项或电阻项的重要程度,对于可忽略的 ESR 影响,最终纹波曲线看起来几乎是正弦曲线,或者在 ESR 贡献较大的情况下将转换为三角波形。
举个栗子吧:
假设我们BUCK电路中的L、C的值已知:
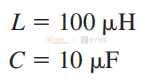
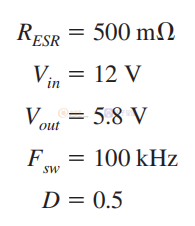
发现 LC 截止频率为 5.03 kHz。 根据上述方程,我们应该得到峰峰值电容纹波值:

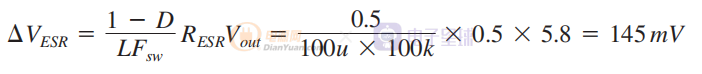
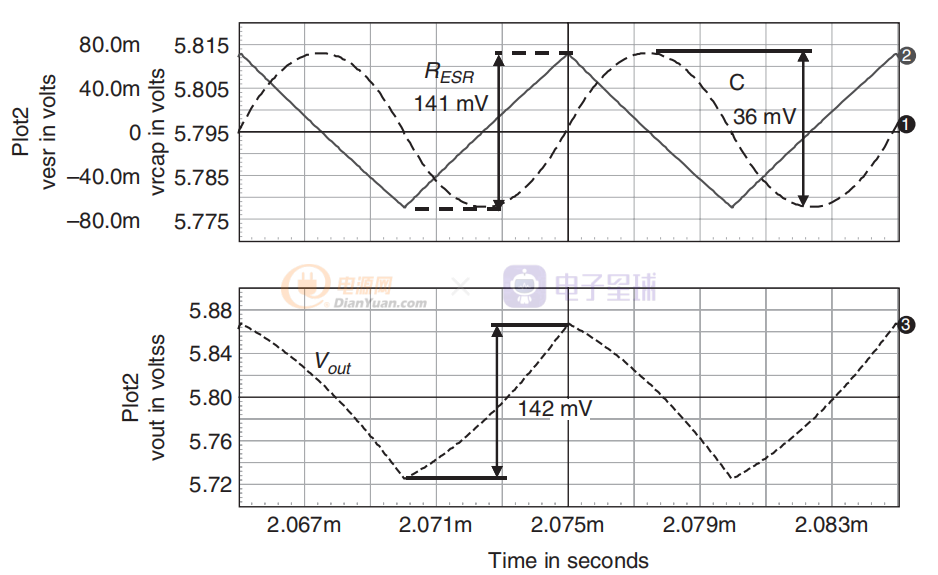
上图中给出了仿真结果并证实了我们的方法。 在这个例子中,我们可以看到每个术语的贡献。 然而,由于 ESR 在纹波表达式中占主导地位,最终波形看起来几乎是三角形的。


