第二节介绍了谐振原理与傅里叶级数推导方法,本节进入正题,讲述LLC谐振拓扑工作过程分析及基波近似法(FHA)推导公式。 本节讲述等效模型化简、直流增益公式和输入阻抗公式的详细推导过程。(本部分为纯数学原理,且篇幅较长,可能有些枯燥,还请大家仔细阅读)
目前市面上所有的资料几乎没有对原理公式的推导过程,初学者也不会对其公式进行推导,如果连公式是怎么来的都不知道,何谈学懂LLC谐振原理,又怎么能设计性能优异的电源呢?
为鼓励作者,快来关注、收藏、分享、点赞、评论一键五连吧,精彩不容错过。
3.1 基波近似等效法(Fundamental Harmonic Approximation,FHA )
对半桥LLC谐振变换器进行稳态分析,主电路拓扑如3-1所示。

图3-1 半桥LLC谐振变换器主电路
假设如下:
⑴ 功率管为理想元件,寄生参数不影响谐振;
⑵ 谐振电路的电感、变压器、电容等均为理想元件;
⑶ 忽略电路中的高次谐波,只有基波传输能量;
⑷ 输出滤波电容值足够大,输出电压无纹波。
图3-1中开关电路将输入的直流信号转换为方波信号,谐振电路可以滤除高次谐波。谐振回路施加的为方波电压,但只有正弦电流流过谐振电路,由于谐振的作用,谐振电路中电流相位滞后于电压相位一定角度,该条件为高压侧功率管零电压(ZVS)开通创造条件。变压器初级输入电压为方波信号、电流为正弦波信号,假设方波信号的能量主要由基波分量传输,利用基波近似等效法(FHA)推导负载阻抗表达式。简化电路如图3-2所示。
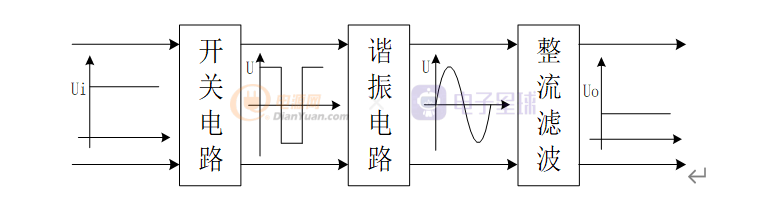
图3-2 主拓扑简化电路
开关电路将直流电压转换为高频方波,桥臂中点处电压值为Ui或0。利用傅里叶级数将方波电压展开:
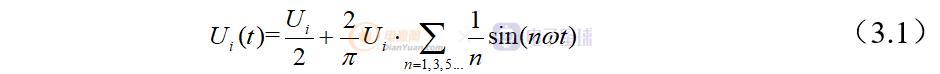
式中,Ui为方波电压幅值。

谐振电路滤除高次谐波,谐振腔中电流为正弦波,且电压相位超前电流相位一定的角度,为零电压(ZVS)开通做准备。

式中,Ir为电流有效值,φ为谐振电流与基波电压的相位差。
变压器低压侧输出电压为方波、电流为正弦波,其电压幅值为±Vo。波形如图3-3所示。
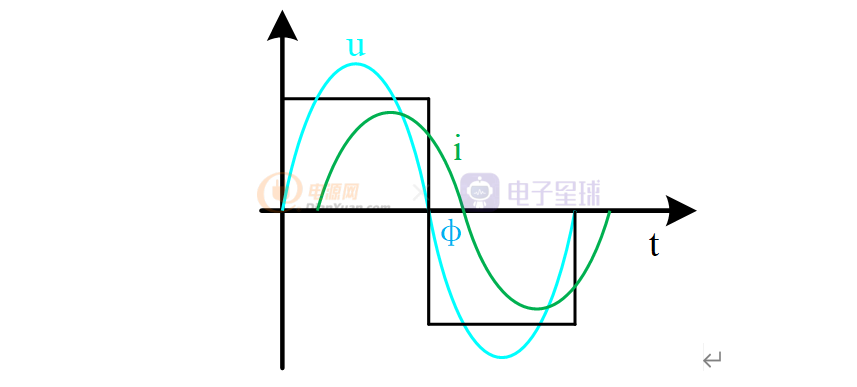
图3-3 低压侧电压电流波形
假设负载为阻性,低压侧电流和电压波形相位一致,即φ=0。电压的傅里叶展开式为:

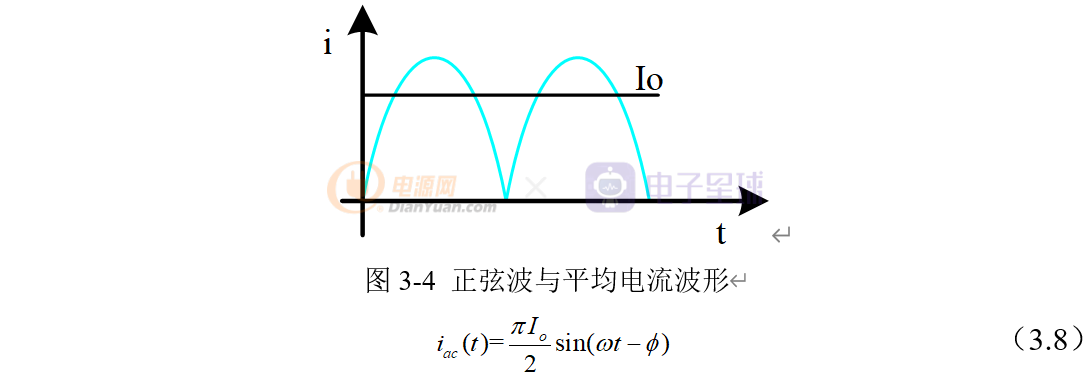
式中,Io为输出电流平均值。
等效交流负载:

直流增益方程推导





输入阻抗公式推导


阻性分割线公式推导

傅里叶级数参考资料
【1】boy59.图解傅里叶变换.电源网论坛(点击可看)
【2】Heinrich.傅里叶分析之掐死教程.知乎(点击可看 )


