接着上一篇!
我们现在将从面向详细电路的分析方法转变为对降压功率级进行更多系统级研究。 本文将帮助电源设计人员准确建模作为降压电源控制环路组件的功率级的技术。 电源控制环路的三个主要组件(即功率级、脉宽调制器和误差放大器)以框图形式显示在图 7 中。

图7 功率电源控制环路补偿
功率级建模是电源设计人员面临的主要挑战之一。 一种流行的技术涉及仅对功率级的开关元件进行建模。 推导出这些元件的等效电路,称为 PWM 开关模型,其中 PWM 是脉冲宽度调制的缩写。 此处介绍了这种方法。
如图 7所示,功率级有两个输入:输入电压和占空比。 占空比是控制输入,即这个输入是一个逻辑信号,它控制功率级的开关动作,从而控制输出电压。即使降压功率级具有基本线性的电压转换比与占空比,许多其他 功率级具有非线性电压转换比与占空比。 为了说明这种非线性,图 8显示了升压功率级的稳态电压转换比与稳态占空比 D 的函数关系图。这里使用非线性升压功率级进行说明以强调 推导线性模型的重要性。
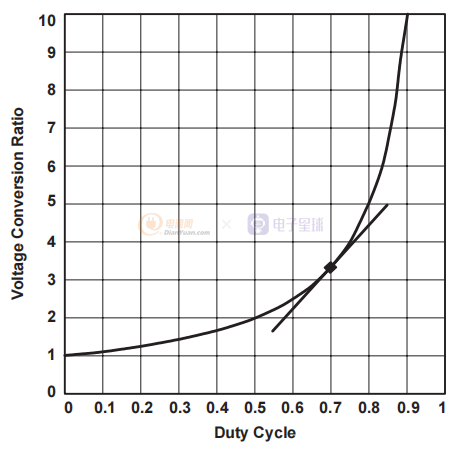
图8 提升非线性功率级增益与占空比
非线性特性是功率级开关元件 Q1 和 CR1 开关动作的结果。 功率级中唯一的非线性元件是开关器件; 电路的其余部分由线性元件组成。 通过在一个开关周期内对与这些非线性分量相关的电压和电流进行平均,可以导出仅包含非线性分量的线性模型。 然后将该模型代入原始电路以分析完整的功率级。 因此,给出了开关器件的模型,称为 PWM 开关模型。
功率级建模背后的基本目标是表示给定工作点的交流行为,并在工作点附近呈线性。我们需要线性,以便我们可以应用许多可用于线性系统的分析工具。 再次参考图 8,如果我们选择 D = 0.7 处的工作点,则可以构建一条直线,该直线与 D = 0.7 处的原始曲线相切。 这是关于工作点的线性化的说明,这是一种用于推导 PWM 开关模型的技术。 定性地,人们可以看到,如果占空比的变化保持很小,线性模型可以准确地表示所分析的功率级的非线性行为。
一、BUCK变换器CCM模式小信号分析
为了开始对降压功率级建模,我们从 (CCM) 中 PWM 开关模型的推导开始。 我们专注于图 1 中所示的 CCM 降压功率级。该策略是在一个开关周期内平均开关波形,并生成等效电路以替代功率级的其余部分。 平均的波形是 CR1 两端的电压 vc–p 和 Q1 中的电流 ia。 波形如图 3 所示。
再次参考图 1,功率晶体管 Q1 和钳位二极管 CR1 绘制在虚线框内。 这些元件将被 PWM 开关等效电路取代。 标记为 a、p 和 c 的端子将用于 PWM 开关模型的端子标签。
现在,对终端命名约定的解释是有序的。 名为 a 的终端用于活动; 它是连接到有源开关的终端。 同理,p 代表无源,是无源开关的端。 最后,c 表示公共端,是有源和无源开关共有的端子。有趣的是,所有三种常用的功率级拓扑都包含有源和无源开关,并且也可以应用上述端子定义。 此外,将我们将派生到其他功率级拓扑中的 PWM 开关模型替换为该特定功率级的有效模型,确实如此。 要在其他功率级中使用 PWM 开关模型,只需将下面图 10 中所示的模型替换为适当方向的功率级。
参考图 3 中的波形,视为时间的瞬时函数,以下关系成立:

其中:ia(t) 和 ic(t) 是开关周期内的瞬时电流,vcp(t) 和 vap(t) 是指示端子之间的瞬时电压。
如果我们取上述量的一个开关周期的平均值,我们得到:
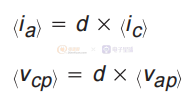
其中括号表示平均值。
现在,我们可以使用相关源在一个简单的电路中实现上述平均方程:
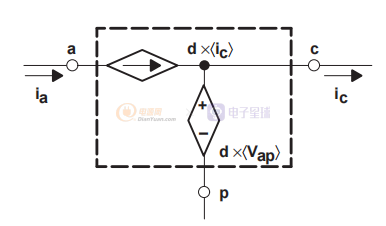
上述模型是PWM开关模型的一种形式。 然而,在这种形式中,它是一个大信号非线性模型。 我们现在需要执行扰动和线性化,然后 PWM 开关模型将处于所需的形式,即关于给定的工作点线性化。
扰动和线性化的主要思想是假设一个工作点并引入关于该工作点的微小变化。 例如,我们假设占空比固定为 d = D(大写字母表示稳态或直流量,而小写字母表示时变量)。 然后将一个小的变化 d^ 添加到占空比,以便占空比的完整表达式变为:

请注意,数量上方的 ^(帽子)代表扰动或小交流量。 我们稍微改变符号,用大写字母(表示直流量)如 Ia 替换平均量如〈ia〉。 现在我们将上述过程应用于等式(1)和(2)以获得:

现在,将稳态量从交流量中分离出来,并且还要去掉交流量的乘积,因为假设变化很小,并且假设两个小量的乘积可以忽略不计。 我们得出稳态和交流关系,或者换句话说,直流和小信号模型:

为了将上述方程实现到一个简单的电路中,首先要注意两个稳态关系可以用一个理想的(与频率无关的)变压器表示,其匝数比等于 D。 源到理想变压器的初级侧。 PWM 开关的直流和小信号模型如图 10 所示。可以很容易地验证下面的模型满足上述四个方程。
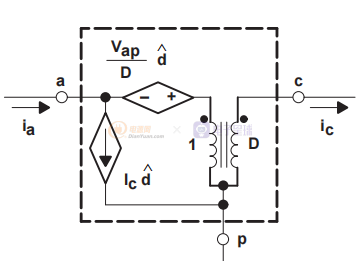
图10 直流和CCM模式PWM开关模型的小信号
该模型现在可以替代降压功率级中的 Q1 和 CR1,以获得适用于直流或交流分析的模型,如图 11 所示。
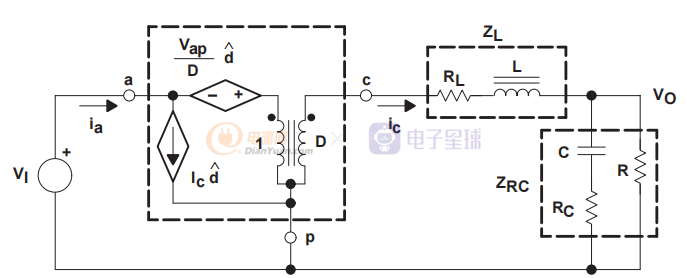
图11 CCM模式稳态模型
为了说明 PWM 开关模型的功率级分析变得多么简单,请考虑以下内容。对于直流分析,d^ 为零,L 为短路,C 为开路。然后通过检查可以看到 VI × D = VO。我们还看到 Vap = VI。因此,知道输入电压和输出电压,很容易计算 D。对于交流分析,可以计算以下传递函数:开环线路到输出、开环输入阻抗、开环输出阻抗和开环控制到输出。控制到输出,或占空比到输出,是最常用于控制环路分析的传递函数。要确定此传递函数,首先,使用 DC 分析的结果获取工作点信息。此信息用于确定相关源的参数值;例如,Vap = VI。然后将输入电压设置为零,因为我们只需要传递函数的交流分量。现在,为 VI 相关电压源 - 变压器初级环路编写电压环路方程给出从占空比到 vcp 的传递函数,如下所示:

从 vcp 到输出电压的传递函数为:
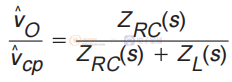
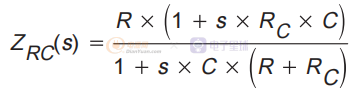
输出 R 和输出 C 的并联组合:
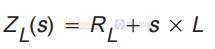
因此,简化后,占空比到输出的传递函数为:

二、BUCK变换器DCM模式小信号分析
为了模拟非连续导通模式 (DCM) 下的降压功率级操作,我们遵循与上述 CCM 类似的路径。 通过更换开关元件,将 PWM 开关模型插入到功率级电路中。 如上所述,DCM PWM 开关模型的推导在别处给出。 更多详细信息可以在电力电子基础知识中找到。 DCM PWM 开关模型的大信号非线性版本如图 12 所示。该模型可用于确定电源的直流工作点。 输入端口简单地用一个电阻器 Re 建模。 Re 的值由下式给出:
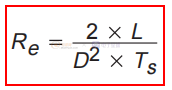
输出端口被建模为从属电源。 该电源提供的功率等于输入电阻 Re 消耗的功率。 该模型类似于图 9 中所示的(非线性)CCM PWM 开关模型。

图12 DCM模式平均的PWM开关模型
为了说明使用该模型的非连续传导模式电源分析,我们检查降压功率级。 分析像 CCM 案例一样进行。 等效电路代入原电路。 DCM 降压功率级模型原理图如图 13 所示。
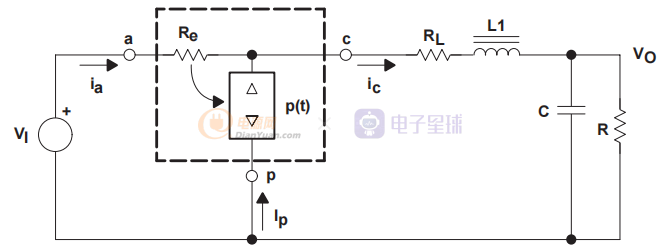
图13 DCM模式BUCK变换器DC稳态模型
请注意,该模型包含电感直流电阻。 为了说明如何使用模型来确定直流工作点,只需写出上述电路的方程式即可。 该电路可以通过所示的网络方程来描述。 首先,将 Re 中的耗散功率设置为从属电源提供的功率:
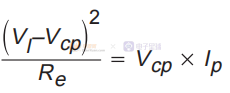
其中电流 Ip 是 IC 和 IA 之间的差值如下:
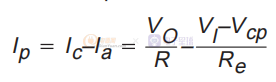
现在,将 Ip 的等式代入以下等式:

现在我们将 VCP 与 VO 关联如下:
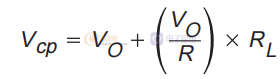
通过从两个方程中消除 Vcp 并使用我们之前对 Re 和 K 的关系,可以求解上述两个方程,以根据 VI 和 D 给出 VO。
DCM 降压的电压转换关系由下式给出:

这类似于我们之前的稳态结果,但包含电感电阻的影响。
为了推导小信号模型,图 13 的电路按照类似于 CCM 推导的程序进行扰动和线性化。 在 DCM 中运行的降压功率级的最终小信号模型如图 14 所示。
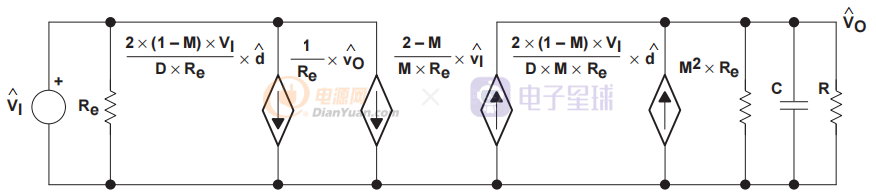
图14 DCM模式小信号
在 DCM 中运行的降压功率级的占空比到输出传递函数由下式给出:


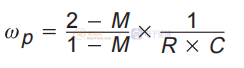
三、电感值确定
先前对降压功率级的分析是针对稳态操作的连续和非连续传导模式。 功率级的传导模式是输入电压、输出电压、输出电流和电感值的函数。 降压功率级可设计为在负载电流高于特定水平(通常为满载的 5% 至 10%)时以连续模式运行。 通常,输入电压范围、输出电压和负载电流由功率级规范定义。 这将电感值作为设计参数以保持连续导通模式。
维持连续导通模式的电感最小值可通过以下程序确定。首先,定义Io(crit)为维持连续导通模式的最小电流,通常称为临界电流。 该值如图 4 所示,计算公式如下:
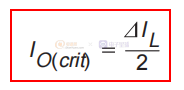
其次,计算 L 以满足上述关系。 为求解上述方程,ΔIL(+) 或ΔIL(–) 可用于ΔIL。 另请注意,ΔIL 的任一关系都与输出电流水平无关。 这里使用了 ∆IL(–)。 最坏的情况(给出最大的 Lmin)是在最大输入电压,因为这给出了最大的 ∆IL。
现在,代入并求解 Lmin:
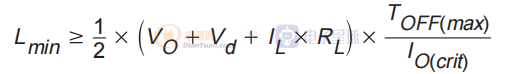
上面的等式可以简化并变成更容易应用的形式,如下所示:

使用刚刚计算的电感值将保证输出负载电流高于临界电流水平 Io(crit) 时的连续导通模式操作。
四、输出电容
在开关电源功率级中,输出电容的作用是储存能量。 由于施加的电压,能量存储在电容器的电场中。 因此,定性地,电容器的功能是尝试保持恒定电压。
通常选择降压功率级的输出电容值以将输出电压纹波限制在规范要求的水平。 由于输出电感中的纹波电流通常已经确定,因此电容器的串联阻抗主要决定了输出电压纹波。 影响其阻抗(和输出电压纹波)的电容器的三个元素是等效串联电阻 (ESR)、等效串联电感 (ESL) 和电容 (C)。 下面给出了输出电容器选择的指南。
对于连续电感电流模式操作,为了确定作为电感电流纹波 ∆IL、开关频率 fS 和所需输出电压纹波 ∆VO 的函数所需的电容量,使用以下等式假设所有输出电压纹波 是由于电容器的电容。

对于不连续电感电流模式操作,为了确定作为电感电流纹波 ∆IL、输出电流 IO、开关频率 fS 和输出电压纹波 ∆VO 的函数所需的电容量,使用以下等式,假设所有 输出电压纹波是由电容器的电容引起的。
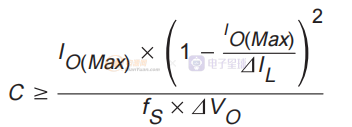
在许多实际设计中,为了获得所需的 ESR,必须选择比所需电容大得多的电容器。
对于连续或不连续电感器电流模式操作,并假设有足够的电容使得电容引起的纹波可以被忽略,则将纹波限制为 ∆VO V 峰峰值所需的 ESR 为:
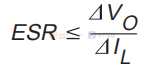
流经电容器 ESR 的纹波电流会导致电容器功耗。 这种功耗会导致电容器内部的温度升高。 温度过高会严重缩短电容器的预期寿命。 电容器的纹波电流额定值取决于环境温度,不应超过。 参考图 3,输出电容纹波电流是电感电流 IL 减去输出电流 IO。流经输出电容的纹波电流的 RMS 值(连续电感电流模式操作)由下式给出:
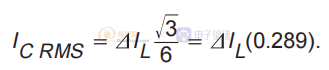
ESL 可能会因为在低兆赫兹区域引起振铃而成为一个问题,但可以通过选择低 ESL 电容器、限制引线长度(PCB 和电容器)以及用几个并联连接的较小设备替换一个大型设备来控制。
三种电容器技术——低阻抗铝、有机半导体和固体钽——适用于低成本的商业应用。低阻抗铝电解液成本最低,体积小,电容高,但 ESR 高于其他两种。 有机半导体电解液,如三洋 OS-CON 系列,已成为电源行业中非常受欢迎的最近几年。这些电容器兼具两全其美——在整个温度范围内保持稳定的低 ESR 和小型封装中的高电容。大多数 OS-CON 单元采用引线安装的径向封装;表面贴装器件可用,但牺牲了大部分尺寸和性能优势。如果必须使用表面贴装设备,则固态钽芯片电容器可能是最佳选择。 AVX TPS 系列和 Sprague 593D 系列等产品专为电源应用而开发。这些产品提供在温度范围内相对稳定的低 ESR、高纹波电流能力、低 ESL、浪涌电流测试和高电容体积比。
下一篇我们将介绍功率器件相关的选型计算。


