上一篇我们对LLC的模型进行分析和等效模型的建立,本文将根据模型中的电气特性,分析LLC如何工作使得输出稳定的?稳定的输出是由哪些量决定的?这些量之间又存在哪些关系呢?
在了解上述问题之前,我们先要分析一下电气变量的关系。【接上一篇文章】
在输入侧,方波电压(Vsq)的基波电压为:

它的RMS为:

在输出端,由于 Vso 近似为方波,因此基波电压为:
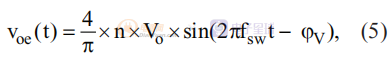
其中 φV 是 Voe 和 Vge 之间的相位角,RMS 输出电压为:

对应于 Voe 和 Ioe 的电流的基波分量是:
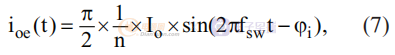
其中 φi 是 ioe 和 voe 之间的相位角,RMS 输出电流为:

那么交流等效负载电阻 Re 可以计算为:

由于图 1b 中的电路是单频正弦交流电路,因此可以按照与所有正弦电路相同的方式进行计算。 角频率为:

化简得到:

Cr、Lr 和 Lm 的容抗和感抗分别为:

励磁电流有效值为:

串联谐振电路中的循环电流为:

建立电气变量的关系后,下一步是进行电压增益函数推导。
自然,输入电压和输出电压之间的关系可以用它们的比率或增益来描述:
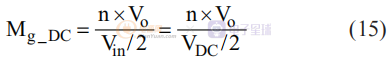
如前所述,将直流输入电压和输出电压转换为开关模式,然后等式(15)可以近似为双极方波电压(Vso)与单极方波电压(Vsq)之比:

交流电压比 Mg_AC 可以通过使用基本分量 Vge 和 Voe 分别代替方程(16)中的 Vsq 和 Vso 来近似:

为简化符号,此处将使用 Mg 代替 Mg_AC。 从图 1b 中,Voe 和 Vge 之间的关系可以用电参数 Lr、Lm、Cr 和 Re 来表示。 然后输入到输出电压增益或电压传递函数变为:

等式 (18) 描述了从输入电压 (Vin) 到输出电压 (Vo) 的连接,该连接与具有 LLC 电路参数的 Mg 相关。 虽然这个表达式只是近似正确,但实际上它足够接近串联谐振附近。 接受近似为准确允许方程(19)写成:

换句话说,可以在知道 Mg、n 和 Vin 之后确定输出电压。
电压增益函数的归一化格式
等式 (18) 描述的电压增益函数以具有绝对值的格式表示。 很难对这种格式的设计问题进行一般性描述。 最好用规范化的格式来表达。 为此,可以选择串联谐振频率 (f0) 作为归一化的基础。 然后归一化频率表示为:

此外,为了将两个电感合二为一,电感比可以定义为:

串联谐振电路的品质因数定义为:

请注意,fn、Ln 和 Qe 是无单位变量。
在这些定义的帮助下,电压增益函数可以被归一化并表示为:
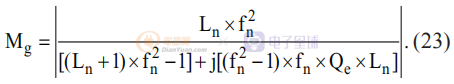
输入和输出电压之间的关系也可以从等式(23)获得:
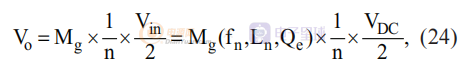
电压增益函数的特性
等式 (23) 表示的电压增益函数和图 1b 中的电路模型构成了本主题所述设计方法的基础; 因此,有必要了解 Mg 如何作为三个因素 fn、Ln 和 Qe 的函数。 在增益函数中,频率 fn 是控制变量。 Ln 和 Qe 是虚拟变量,因为它们在确定物理参数后就固定了。 设计完成后,通过 fn 调整 Mg。 因此,解释增益函数如何表现的一个好方法是在给定条件下从 Ln 和 Qe 的值族中绘制 Mg 与 fn 的关系图。
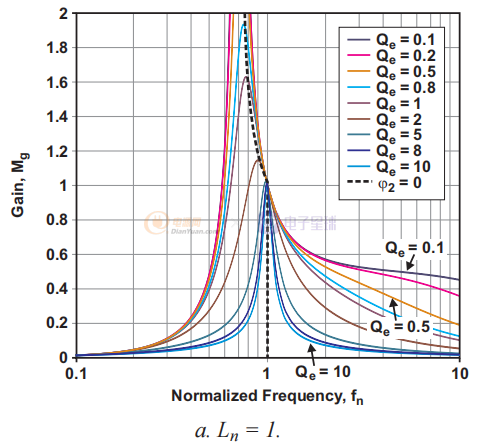
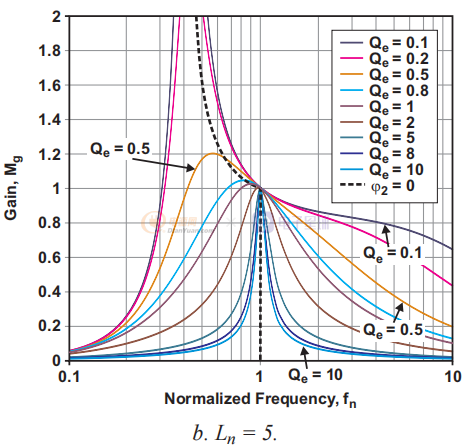
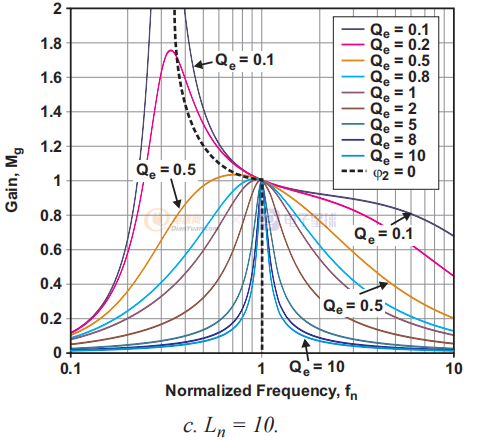

图 2. 具有不同 Ln 值的电压增益函数 (Mg) 图。
图1a到1d说明了几种可能的关系。 每个图都由一个固定的 Ln 值(Ln = 1、5、10 或 20)定义,并针对变量 Qe 显示具有九个值(从 0.1 到 10)的曲线族。 从这些图中,可以得出几个观察结果。
Mg的值不小于零。 这是显而易见的,因为 Mg 来自模数运算符,它描述了一个包含实数和虚数的复杂表达式。 这些数字代表幅度和相位角,但在这种情况下只有幅度有用。
在给定的 Ln 和 Qe 内,Mg 在电路谐振频率附近呈现凸曲线形状。 这是一条典型曲线,显示了谐振转换器的增益形状。 对应于谐振峰值(fn_c0,或 fsw = fc0)的归一化频率随着负载的变化而移动,因此对于给定的 Ln,也随着 Qe 的变化而移动。
改变 Ln 和 Qe 将重塑 Mg 曲线并使其与 fn 不同。 由于 Qe 是由方程 (9) 和 (22) 描述的负载函数,因此 Mg 呈现了一系列将频率调制与负载变化相关联的曲线。
无论使用 Ln 和 Qe 的哪种组合,所有曲线都会收敛并通过 (fn, Mg) = (1, 1) 点。 该点位于 fn = 1 处,或来自公式 (20) 的 fsw = f0。 根据串联谐振的定义,在 f0 处 XLr– XCr = 0。 换句话说,Lr 和 Cr 两端的压降为零,因此输入电压直接施加到输出负载,从而导致单位电压增益 Mg = 1。
请注意,工作点 (fn, Mg) = (1, 1) 与负载无关; 即,只要增益 (Mg) 可以保持一致,无论负载电流是多少,开关频率都将处于串联谐振频率 (f0)。 换句话说,在工作点位于 (fn, Mg) = (1, 1) 或其附近的设计中,频率变化被缩小到最小。 在 (fn, Mg) = (1, 1) 处,假设没有寄生功率损耗,串联谐振电路的阻抗为零。 然后,无论负载电流变化多少,整个输入电压都会施加到输出负载。 然而,远离(fn, Mg) = (1, 1),串联谐振电路的阻抗变为非零,电压增益随着负载阻抗的不同而变化,相应的操作变得依赖于负载。
对于固定的 Ln,增加 Qe 会缩小曲线,导致频率控制带变窄,这是预期的,因为 Qe 是串联谐振电路的品质因数。 此外,随着整条曲线向下移动,Mg的对应峰值变小,对应于该值的fn向右移动并接近fn=1。这种随着Qe增加的频移是由于负载增加。 回顾方程 (9) 和 (22) 很明显Qe 的增加可能来自 RL 的减少,因为 Lm 和 Lr 都是固定的。 对于相同的串联谐振频率,Cr 也是固定的。 RL 与 Lm 平行,因此减少 RL 将减少 Lm 的影响并将 fc0 移向 f0。 作为一个简单的例子,检查两个极端是有帮助的:
1、如果 RL 开路,则 Qe = 0,并且 fc0 = fp,如等式 (2) 所述。 fc0 位于 f0 的最左边,对应的增益峰值非常高,理论上可以无限大。
2、如果 RL 短路,则 Qe = ∞ 并且 Lm 被完全旁路或短路,使得 Lm 对增益的影响消失。 然后来自 Lm 效应的相应峰值增益值变为零,并且 fc0 一直向右移动,与 f0 重叠。
3、因此,如果 RL 从无穷大变为零,则谐振峰值增益从无穷大变为 1,峰值谐振处的相应频率 (fc0) 从 fp 移动到串联谐振频率 (f0)。
对于固定的 Qe,Ln 的减小会缩小曲线; 整个曲线被挤压,fc0 向 f0 移动。 这导致更好的频率控制带具有更高的峰值增益。 有两个原因。 首先,当 Ln 由于 Lm 减小而减小时,fp 越来越接近 f0,从而挤压了从 fp 到 f0 的曲线。 其次,降低的 Ln 会增加 Lr,从而导致更高的 Qe。 如上所述,较高的 Qe 会缩小曲线。
乍一看,Ln 和 Qe 的任何组合似乎都适用于转换器设计,并且可以在 fn = 1 的任一侧运行 fn 来进行设计。但是,下一篇文章会讲述LLC在设计时的更多考虑!


