多输出反激式转换器因其简单和低成本而成为一种流行的拓扑结构。 如果绕组之间的完美耦合是可能的,那么输出电压将直接由它们各自与提供稳压输出的绕组的匝数比来定义。 不幸的是,完美的绕组耦合是不可能的,耦合操作非常复杂,这往往会导致交叉调节不佳。本文就来揭开交叉调整率的神秘面纱!
一、理论分析
有一些已知的交叉调节分析模型。例如,使用物理模型的交叉调节分析相当复杂,但具有几何独立性和其参数可以直接测量等优点。另一方面,图1中所示的物理模型(也称为“梯形”模型)基于这样一个事实,即变压器绕组由于它们之间的物理分离而无法全部都很好地耦合到储能间隙。此外,额外量的磁能存储在绕组之间并表示为漏电感。尽管不适用于任何变压器几何结构,但该模型是帮助了解大多数常见反激变压器几何结构如何工作的好工具。图 1中的电路表示仅适用于所示的变压器绕组叠层。如果使用交错或同时缠绕多个次级绕组(多股),则需要更复杂的电路表示。此外,该模型在评估轻载次级输出时确实缺乏准确性。
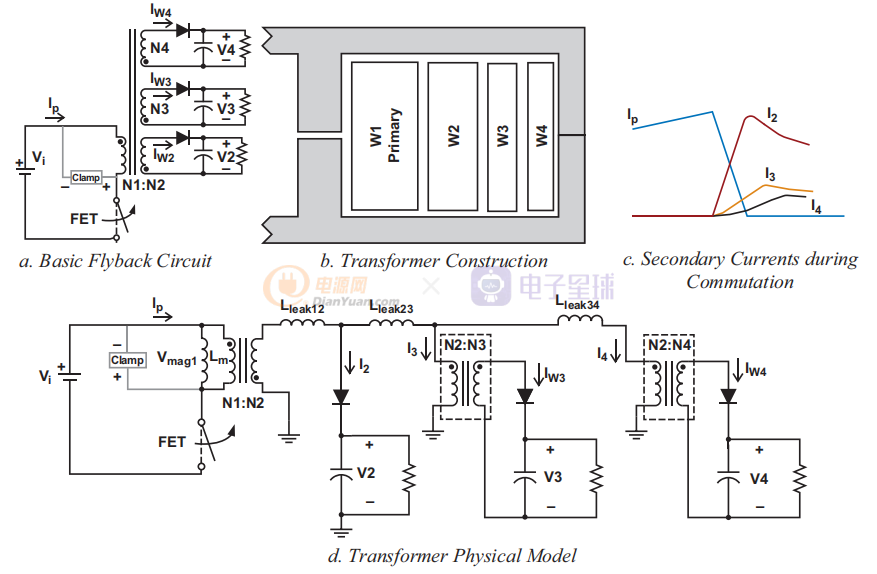
图1 具有理想化次级电流波形的基于物理模型的反激交叉调节(所有输出均处于满载状态;不包括绕组电阻和寄生电容效应)。
在换向过程中,间隙中的磁通量 (φm) 会降低,从而在次级绕组中感应出电流。 这种感应电流有助于保持间隙中的磁动势 (MMF)。 每个次级绕组内的磁通下降率(包括漏感)受其输出电压的限制,公式如下:
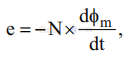
其中 N 是绕组的匝数,e 是其感应电压。
例如,一旦初级电压超过 W2 的反射电压,W2 的电流就会增加,进而产生增加的通量。 由于 W1 和 W2 之间的漏磁通,初级电压上升,直到达到钳位电压。 这定义了间隙中 dfm/dt 的限制。
主次级绕组 (W2) 与初级 (W1) 相邻,决定了外部绕组在换向过程中将看到的 df/dt。 由于 W3 和 W4 位于主输出绕组之后,如果完全没有泄漏,则产生的绕组电压低于预期的电压。 图 1中显示的净效应是,当主开关关闭时,电流从近端到远端的次级绕组逐渐换向。
然而,如果采用交错方式,使 W1 的一半靠近低功率次级绕组,W1 的部分磁通将不会被 W2 检测到,但会被低功率次级绕组检测到,从而增加了 感应到这些绕组中的电压。
在所示模型中,当所有泄漏都移到变压器的 W2 侧时,Lleak12 对应于 W2 和 W1 之间的漏电感,而 Lleak23 和 Lleak34 分别对应于 W2 到 W3 和 W3 到 W4 之间的泄漏。
二、漏感和寄生电容引起的振铃
大多数现有模型无法准确预测反激变压器的一种行为——主输出满载时辅助绕组的轻载运行。
当主开关关闭时,当主输出负载很重时,初级电流会导致电压迅速上升。 由于变压器漏感和寄生电容(绕组和二极管),次级电压趋于振铃。 如果辅助输出满载,则此振铃被钳位。 然而,在轻负载时,这种振铃开始通过输出整流器将输出存储电容器充电至振铃电压过冲,从而阻止能量返回。 在轻载时,这会导致辅助输出电压高得多,有时甚至会超过其标称值的两倍。 随着初级钳位电压升高,这种影响通常会变得更糟。
对于反激电源来说,轻负载交叉调节问题可以通过最小化次级绕组之间的漏电感来减轻,但不能消除。 它还有助于找到最靠近初级的最高功率次级。 处理此问题的其他解决方案包括使用后置稳压器、串联电阻或最小负载。
三、工作影响
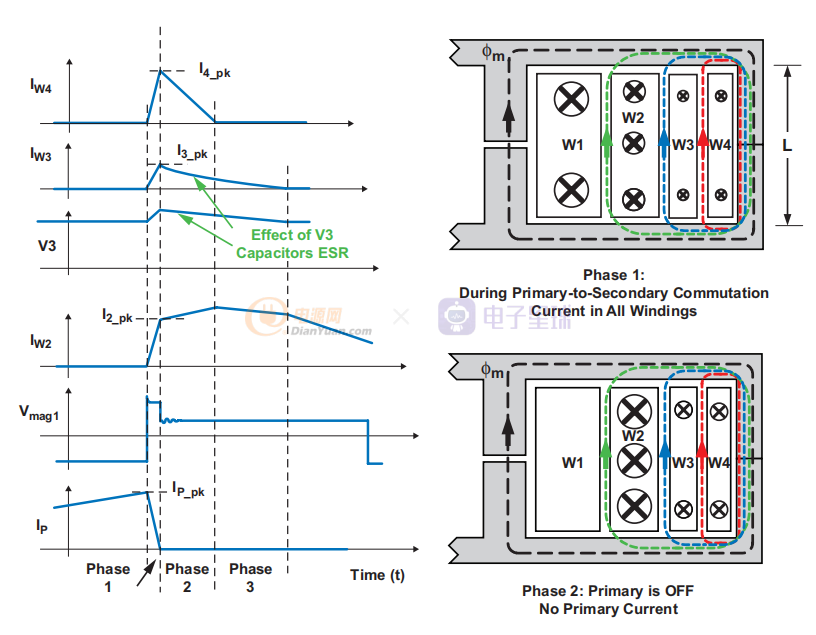
图2初级开关关断时的交叉调节阶段
与图 1 相对应,图 2 显示了从初级到次级换向期间前三相的示例。 出于描述的目的,假设W2是大电流绕组,I2_pk不够高,因为Lleak21太大,W4在换向过程中因为轻载振铃接收太多能量。 W3 和 W4 是低电流辅助次级绕组。
与正激变压器不同,在反激变压器中,初级和次级绕组仅在换向期间同时产生磁通; 该通量是磁化通量。 另一个区别是,在换向期间,间隙内每个绕组产生的磁通方向相同,因为在初级绕组电流逐渐下降时,所有绕组都试图保持磁化通量。 因此,在绕组之间的间距(泄漏)中产生的磁通线彼此相对。 请注意,沿特定路径的漏磁通幅度与 S(N × I) 和两层之间的间距成正比,与图2 所示窗口区域的尺寸 L 成反比。
如前所述,在换向过程中,磁通量 (φm) 的减少会在次级绕组中感应出上升的电流。 由于 W1 和 W2 之间的泄漏,初级电压上升直到达到钳位电压,这定义了间隙中 dfm/dt 的限制。 钳位电压越低,次级绕组中的感应电压越低,其中的 di/dt 越软。 如果没有初级钳位电路,转换到 W2 次级将是瞬时的,但 MOSFET 会被电压应力破坏。
在阶段 1 结束时,反射的次级电流之和等于总磁化电流:
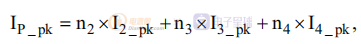
其中 Ix_pk 和 nx 分别是换向间隔结束时的电流和次级绕组数 x 的初级与次级匝数比。
从第 2 阶段和开关周期的剩余时间 (1 – D) 开始,次级电流以取决于反射输出电压之间差异的速率增加或减少。 在此示例中,假设 I4_pk 变得太高,并且 V4 的输出电容器在阶段 1 期间接收了过多能量。在阶段 2 开始时,一部分磁通来自 W4,并开始以 W4 电压定义的速率下降 . 此外,W2 的贡献增加以保持间隙中的磁化通量。 在此期间,IW4 下降,直到它过零并因二极管而停止下降。 如果一个输出负载很轻,它的电压会在换向过程中显着增加。 这意味着在第 1 阶段之后电流下降更陡峭(更快)。
每个输出端的负载会极大地影响交叉调节。 输出电容器 ESR 也具有不可忽略的影响,因为它会随着电流减小而改变斜率。 电流越小,ESR 电压和漏电感两端的电压将越低,这意味着 di/dt 越低。 图 2中 V3 和 IW3 的波形展示了这一概念。
当 IW4 过零时 IW2 的斜率变化可以用以下公式解释:
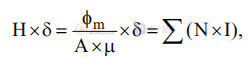
其中 H 是磁场,δ 是磁芯间隙,φm 是磁化通量,A 是磁芯横截面,μ 是磁隙磁导率,N × I 是绕组的安匝数。 公式显示下降的磁化通量 (fm) 对应于所有有源绕组共享的下降的磁化电流。
显然,在 CCM 中操作主输出(使用同步整流器是一个例子)保证了 Vmag1 在 (1 – D) 期间保持不变,有助于实现更好的交叉调节。
后续文章我们讨论如何优化交叉调整率的具体措施。


