漏感是由变压器中一个绕组的磁通量引起的,该磁通量不耦合到其他绕组。 这是由于绕组之间的空间和间隙中的磁通量将能量存储在这些间隙中,就像能量存储在铁氧体磁芯的气隙中一样。 漏感中的能量通常耗散到变压器外部。
对于反激变压器,最小化漏电感非常重要,因为在大多数情况下漏电感 能量在外部缓冲器或钳位电路中耗散。 正如您稍后将看到的,将漏电与磁化电感的比率降至最低以最大限度地减少钳位电路损失的磁化能量也很重要。
一、如何估计和最小化漏电感
几种已发表的方法解释了如何根据绕组的物理几何形状和变压器中的层结构来估计漏电感。 图 1和公式显示了使用夹层的方法。 此方法假设所有绕组层的全宽 b 相同,并且不能与某些部分宽度的层一起使用。 请注意,任何部分宽度层的漏电感都会高得多,随着部分层宽度变窄而增加。

以下是公式的参数:
• N = 与泄漏有关的绕组匝数
• MLT = 每匝绕组的平均长度
• Σh = 所有绕组层的高度总和
• Σc = 绕组层间距的高度总和
• m = 交错级别(绕组“部分”的数量)
• b = 骨架绕线宽度(绕线层的宽度)
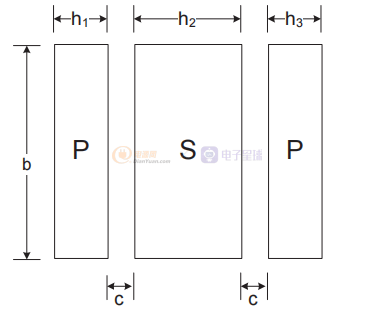
图1 典型的交错式反激变压器绕组层间距
根据 Dowell 方程中使用的假设,圆形线径 d 的每个绕组层都转换为相同横截面的等效矩形块。 因此,h 与 d 并不完全相同:
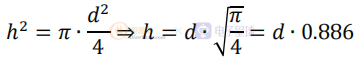
如图 2所示,您可以使用线径和公式来计算每个绕组层的 h。 您可以使用中间胶带或绝缘体的厚度,加上电线上的厚度或漆包覆层或任何其他绝缘体,再加上由于直径 d 转换为等效的 h 而产生的额外间隙,从而计算间距 c。
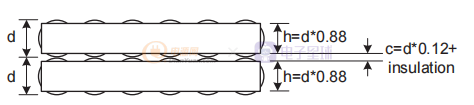
图2 将每个绕组层对转换为等效的 h 和 c
二、漏电感减少和最小化
漏感很大程度上取决于物理绕组几何形状; 您可以根据此几何形状估算漏电感。 可以通过以下方式降低漏电感:
• 交错——增加m 的值。
• 使用更宽的绕线宽度——最大化b。
• 最小化圈数 N 和每圈平均长度 MLT。
• 最小化绕组层之间的间距cn 的厚度和数量。
• 最小化绕组层厚度、hn 和层数。
三、交错
图3显示了在传统前向模式环境中降低漏电感的不同级别交错的示例变压器。 但同样的原理也适用于转换间隔期间的反激式变压器,此时初级和次级电流同时流动,以及漏感相关时。
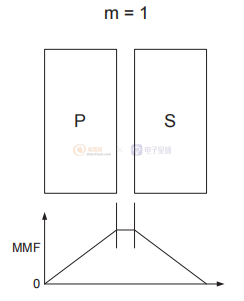
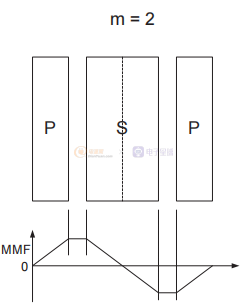
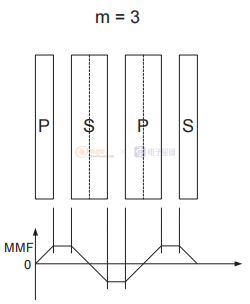
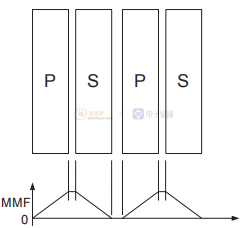
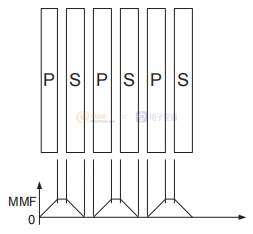
图3 不同级别的交错以减少漏感。
在第一个示例中,初级和次级并排放置,没有交错。 下面相应的 MMF 图显示了主要 MMF 如何建立到最大值,然后被次要 MMF 取消,回到零。 MMF 图仅显示 MMF 的一部分或区域累积并返回零 - 因此在此示例中,只有一部分,m = 1。
主要和次要在第二个示例中交错。 两种交织方法不同,但等效。 这是因为在这两种情况下,MMF 在两个不同的部分建立一个峰值并下降回零,所以在这两种情况下 m = 2。类似地,第三个例子显示了两种不同的交织方法,但两者在 交错部分,两种情况下 m = 3。
由于漏电感与 m2 成反比,因此预计第一级交错两部分(即 m = 2)会导致漏电感降低四倍。 通过从 m = 1 更改为 m = 2,如图3所示,绕组结构从单个初级 - 次级界面变为两个界面,次级的每个面都有一个界面。 在交错情况下,现在有两个界面间距间隙,c; 在非交错情况下,两者的维度可能与单个 c 的维度大致相同。 所以实际上,公式中的因子 Σc/m2 只减少了两倍,而漏电感实际上只减少了一半。 尽管如此,这是一个显着的减少,通常是非常有益的。
然而,设计人员应该意识到,初级和次级绕组交错可能会增加变压器成本,使 EMI 和安全合规性变得复杂(因为现在有两个初级 - 次级接口),并增加变压器绕组间电容。
四、漏电感估计 - 工作示例
我们现在使用公式来估计图4中所示的典型反激式变压器绕组结构的漏电感。该结构由分离的初级和夹在中间的辅助偏置层和次级层组成。 每个半初级缠绕在两层上,次级和偏置层缠绕在单层上。 在次级和外半初级之间还有一个屏蔽层。 图 4列出了所有电线尺寸。

图4交错式反激变压器绕组结构。
我们将所有圆形线径转换为具有相同横截面的等效矩形块。 目标设计的开关频率为 60 kHz,δ ~0.31 mm。 屏蔽层足够薄(0.05 毫米,δ 的六分之一),因此为简单起见,我们将其作为次级和外半初级之间的绝缘空间的一部分(图 5)。
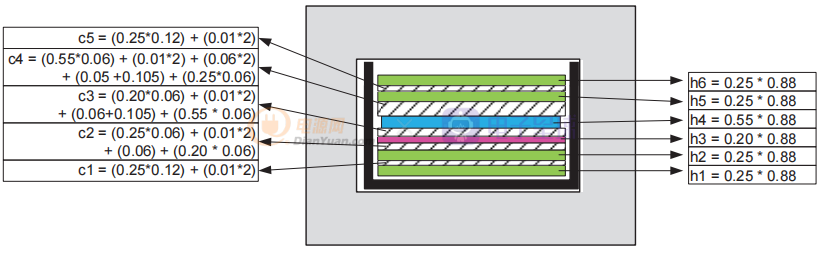
图5 样品交错反激式变压器绕组结构到层高hn和间距cn的转换。
当您知道所有导电层的高度 hn 和绝缘层的间距 cn 时,您可以使用公式估算漏电感。在这种情况下,初级总匝数 N = 34; 我们使用了 RM10 线轴,MLT = 52 毫米。 原版由两部分交错,m = 2; 绕组宽度 b = 9 mm。 (线轴标称尺寸实际上是 10 毫米,但由于导线绝缘和入口/出口导线布线,层填充通常是可用宽度的 90%)。

在公式中,2.71 µH 与测得的 3.2 µH 漏电感相当接近。 差异归结为实际绕组的实际非理想性,例如胶带压痕、入口/出口厚度和返回线。 尽管如此,我们已经展示了如何估计给定绕组结构的漏电感,以及如何客观地比较不同绕组结构的漏电感性能。 我们还展示了所选骨架形状/几何形状对漏电感的影响。
五、钳位电压值对变压器漏感损耗的影响
在单开关反激式转换器中,您通常需要一个钳位电路来限制开关的漏极电压; 钳位电路吸收存储在变压器漏电感中的能量,并且根据钳位电压的值,还会吸收一小部分磁化能量。在图 6 中,您可以看到晶体管 Q 关断后,所有的 初级电流转移到钳位电路(在图6中由电压源 VCLAMP 表示)。 漏电感 LLEAK 上将产生电压,该电压等于 VCLAMP 和反射次级电压 VREFLECTED 之间的差值。 因此,漏电感中的电流(也是初级电流)将以取决于两个电压差的速率下降; 因此,磁化电流将流入钳位电路,直到初级电流衰减为零。
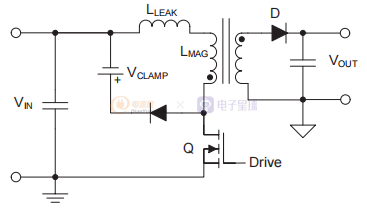
图6 简化的反激原理图,显示了作为理想电压钳位的钳位/缓冲器网络
漏电感中电流减小的速率决定了电流转移到次级的速率。 图7说明了这个过程。
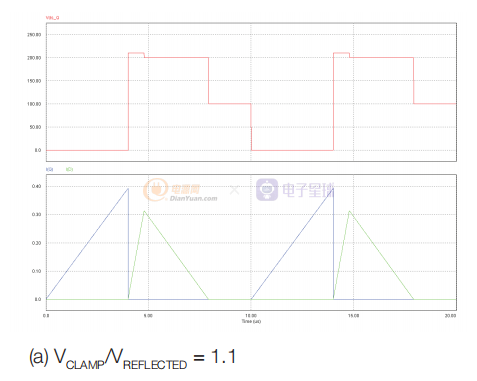

图7 到次级绕组的电流传输 (a) 与电压钳位 (b) 的比较
在图 7a 中,钳位电压仅比反射的次级电压高 10%,在钳位中损失了大量的磁化能量。 与图 7b 相比,传输到次级的电流明显较低,其中钳位电压比反射的次级电压高 50%。
在极端情况下,反射的次级电压等于钳位电压,没有电压可用于 迫使漏电感中的电流比磁化电感中的电流衰减得更快; 因此,没有磁化电流可以传输到次级。 钳位电路将吸收所有磁化能量和泄漏能量。
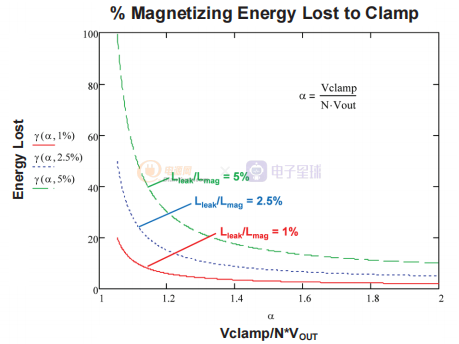
图8 钳位能量损失百分比与钳位电平和漏感/磁化电感比的图表。
图 8显示了钳位中磁化能量损失的百分比 γ,它是钳位电压与初级反射电压之比 α 以及漏电流与磁化电感的百分比的函数。
钳位中的能量损失 随着钳位与反射电压的比率下降到 1.2 以下,它迅速增加。 这种损耗对漏磁电感比也非常敏感。
虽然选择较低的钳位电压可能允许使用具有较低 RDS(on) 的低压开关晶体管,但增加的钳位损耗很容易超过预期的好处。


