给大家简单讲讲在BUCK变换器基础上发展出来的正激、半桥、推挽和全桥PWM变换器多路输出中常采用的耦合滤波电感的工作原理。因为水平有限,只能用仿真软件来简单介绍一下工作原理和设计思路。
常见的PWM控制的正激、半桥、推挽和全桥,其实质还是一个buck变换器。为了简化分析过程,变压器前面的部分我就不说了。仅仅从变压器后面部分开始说明。
对于多路输出的电源,通常变压器次级有多个绕组,按照不同的输出电压要求,绕组的匝数按照相应的比例来设计。但是反馈回路一般只有一个,而且通常是取功率输出最大的那一路来反馈。
假设有这么一个正激电源,输出为:
- 5V/10A
- 3.3V/20A
实际电源中,反馈回路是从3.3V这路取样。
再假设每路输出的整流管都是二极管,压降为0.5V。
再假设如下参数:
- 开关频率f=50KHz
- 满载占空比,低压输入时为Dmax=0.4
- 高压输入时为Dmin=0.2
那么根据这些参数,我们可以来计算每一路的滤波电感的数值应该为多少,假设电流的纹波为20%,根据工作原理,最大电流纹波出现在最高输入电压最大输出负载时:

由此我们也可以知道变压器次级5V绕组和3.3V绕组之间的匝比关系为:
n=13.75/9.5=1.447
有了以上参数,我们就可以建立一个简单的电路模型来模拟双路输出的正激变换器的次级部分了。为了简单起见,我们采用开环控制,这样的话,输出一开始会有过冲,我们可以等稳定以后再分析数据,忽略前面过冲的部分。实际电路由于有反馈环,过冲是不存在的。我们用Vpulse这么模型来模拟次级的变压器绕组输出,二极管采用MBR2540,电感和电容都是采用的理想元件,没有考虑ESR等杂散参数。建立如下电路图,模拟在最低输入电压两路都是最大输出时的状态:
然后如下参数设定时域扫描

扫描完成后,观察输出电压:

从图上可以看出,待稳定后,输出电压是正常的,满足设计要求。
看看此时两个电感的电流波形,注意要把电压探头删掉,换成两个电流探头,分别放在两个电感输入端,同时把波形图的横坐标展开,观察9.9ms到10ms这部分:
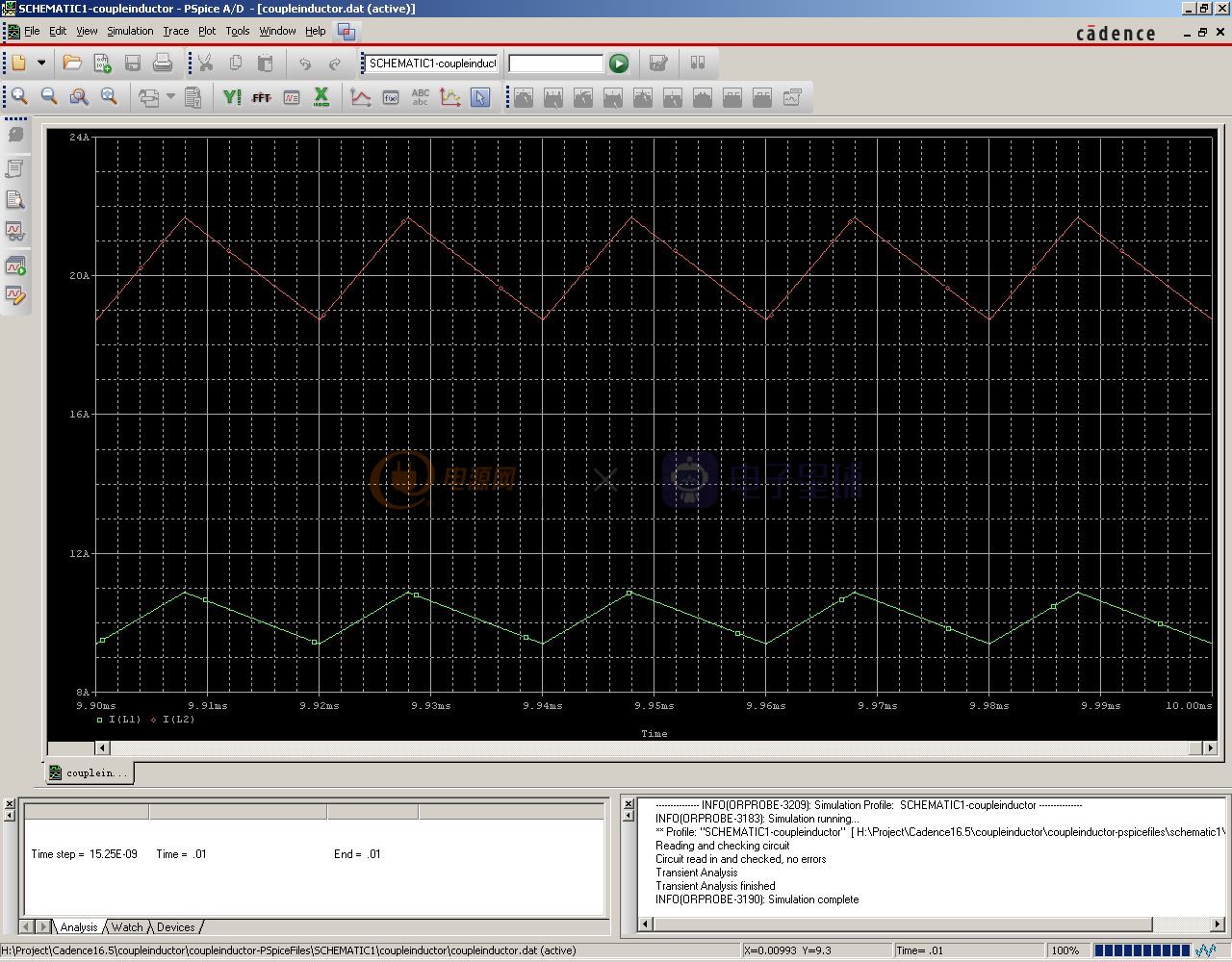
从电感电流波形可以看出,两路输出的电感电流都是处于连续模式的。
现在假设,3.3V输出的负载不变,5V输出的这路输出电流降低,输出电流从10A降到了0.25A,因为实际电源的反馈是取自3.3V输出的。那么由于3.3V这路的输出没有改变。所以电路的工作占空比没有发生变化,那么这时候,会发生什么事情呢?
首先修改5V的输出负载电阻为20欧。
然后,修改时域扫描的时间,把扫描时间增加为20ms,以保证输出完全稳定下来,仿真结束后,如上图再次放上电压探头,看看此时的输出电压是如何变化的:
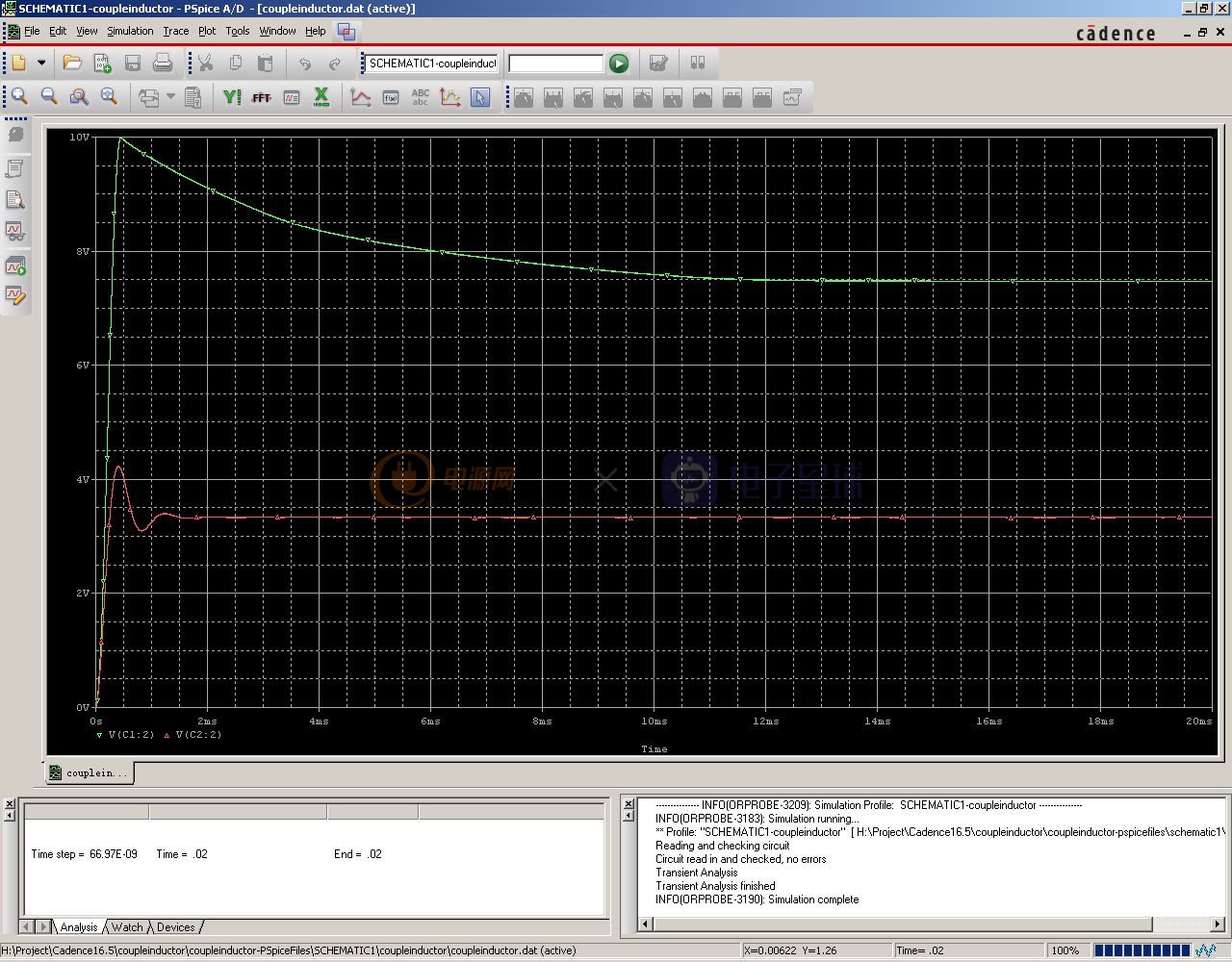
从图中可以看出,3.3V那路的输出还是正常的,而5V那路的输出已经飙升到了7.5V左右。
同样把电压探头删掉,换成电流探头,看看电感电流波形。只不过,这次把时间轴设置成19.9ms~20ms,看看:
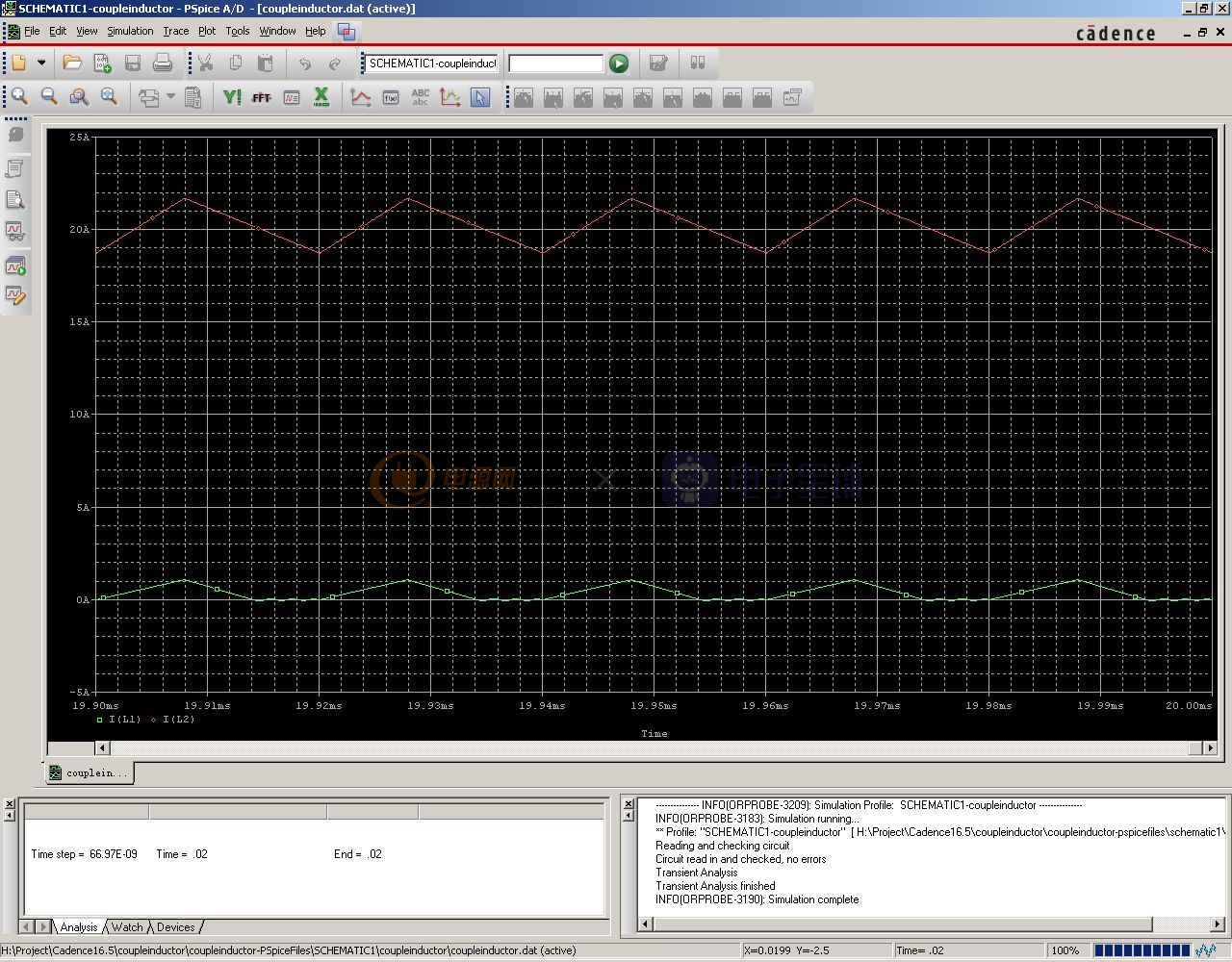
从图中可以看出,5V输出这路,由于负载电流太小,已经进入了DCM模式。那么输出电压已经不再是Vout=Vin×D了。
这就是多路输出,独立滤波电感存在的一个严重问题。为了解决这个问题,就引入了耦合电感这个方法。
在实际设计过程中,通常把所有的输出都折算到某一路输出来计算磁芯的参数,然后按照每路输出电流来选择线径。同时,必须使每路输出电感的匝数比与变压器次级每个绕组的匝数比相同!
我们来尝试计算一下:
假如把5V绕组输出折算到3.3V绕组的输出,那么:
Iout=(5×10+3.3×20)/3.3=35.15A
输出滤波电感应该为
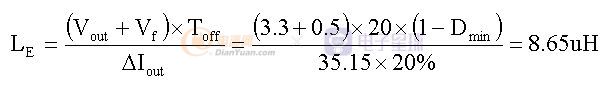
有了这两个数值,我们就可以根据AP法求出实际的磁芯大小。这里我就省略了。
我们前面已经有了5V变压器绕组和3.3V变压器绕组的匝比关系n=1.447,现在根据能量的关系来计算耦合电感的每一路输出的电感量:

把原理图中的两个电感的电感量分别设置为以上参数。然后放置一个耦合元件K_Linear,并将其参数L1、L2分别设置为两个电感的名字l1,l2。设置好负载电阻的阻值:
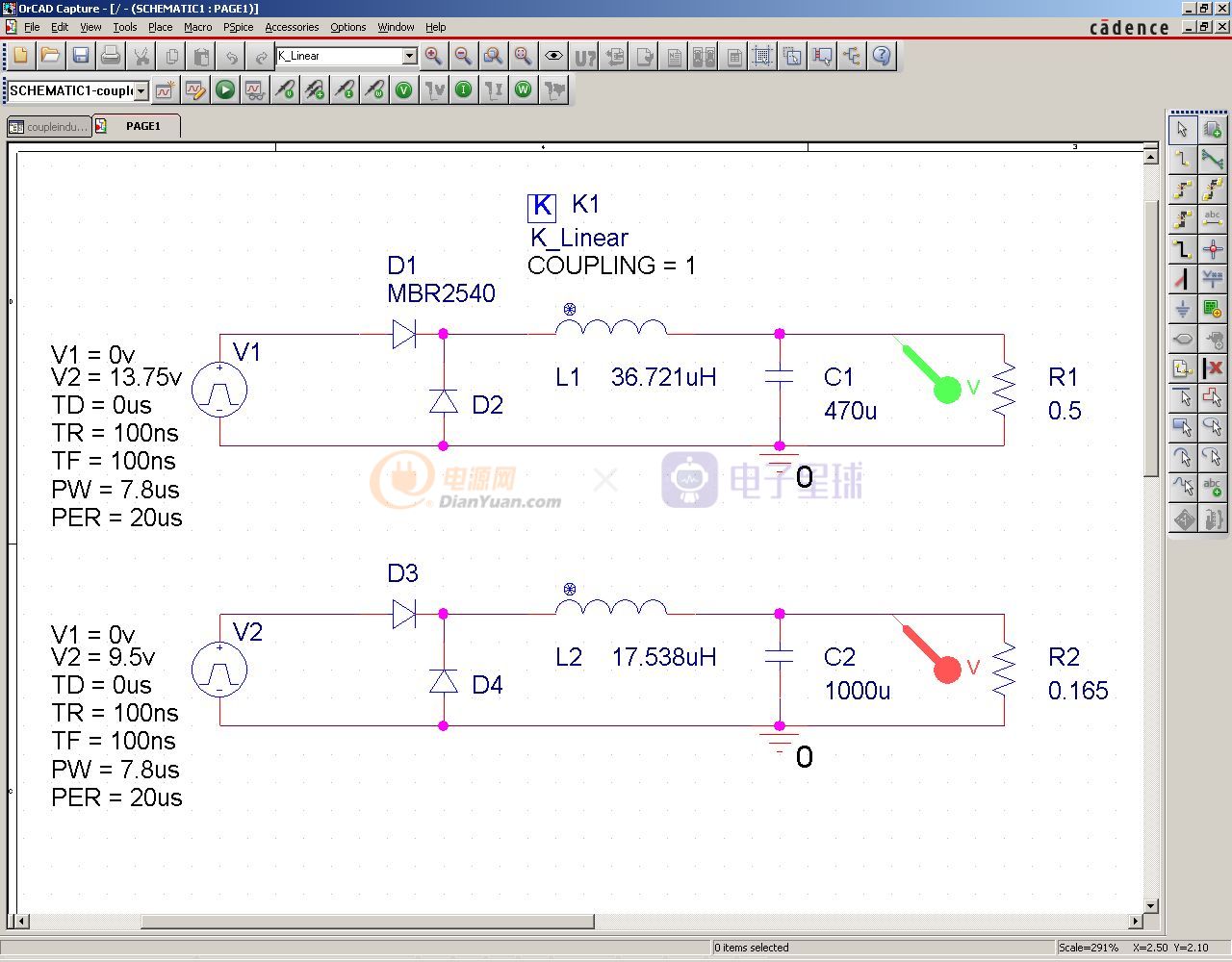
先看看都是满载输出的时候的情况,输出电压:
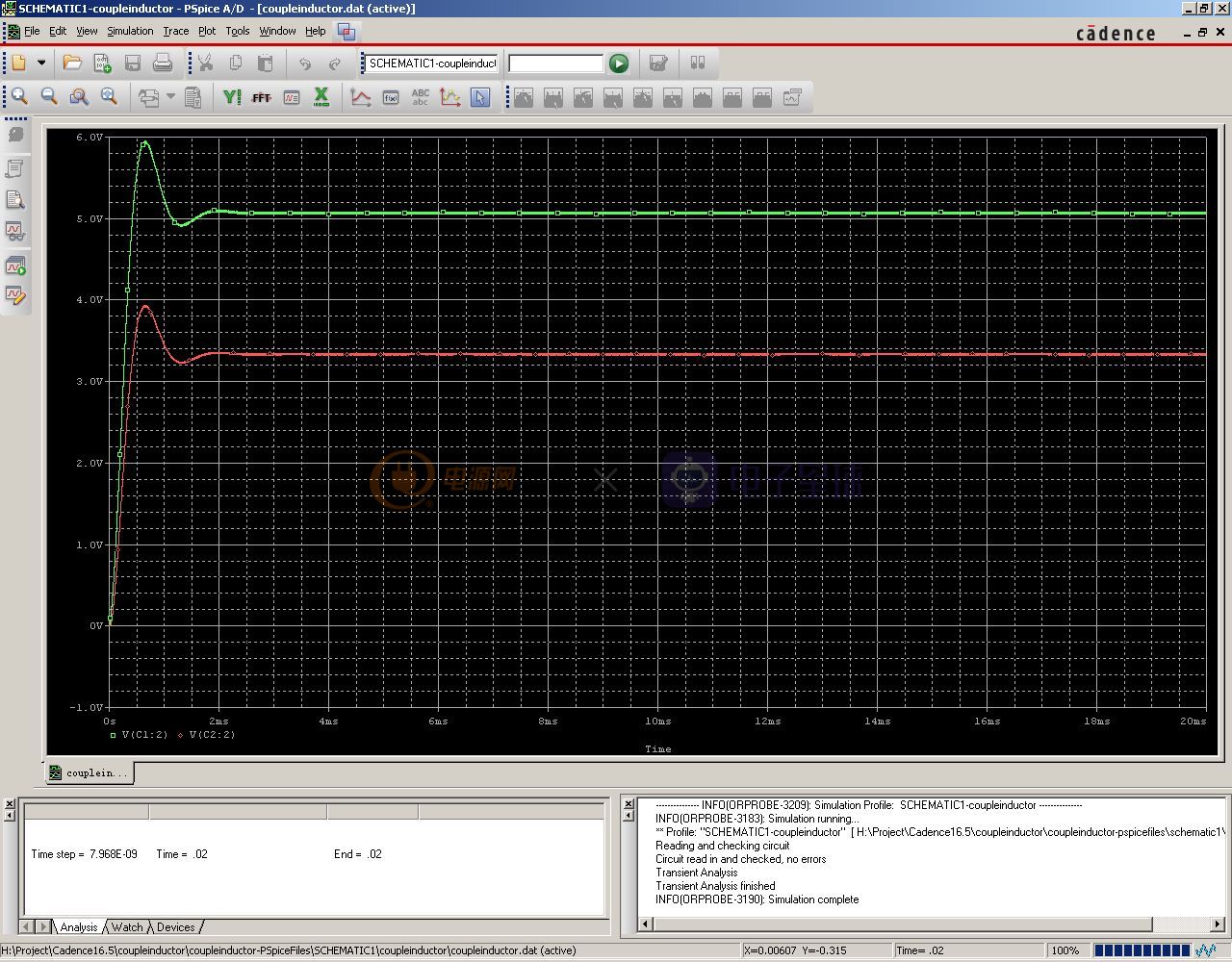
从图中可以看出,输出电压都是正常的,满足设计需要。再看看把5V输出的负载电阻改成20欧的结果会怎么样,下面是仿真后的输出电压波形:
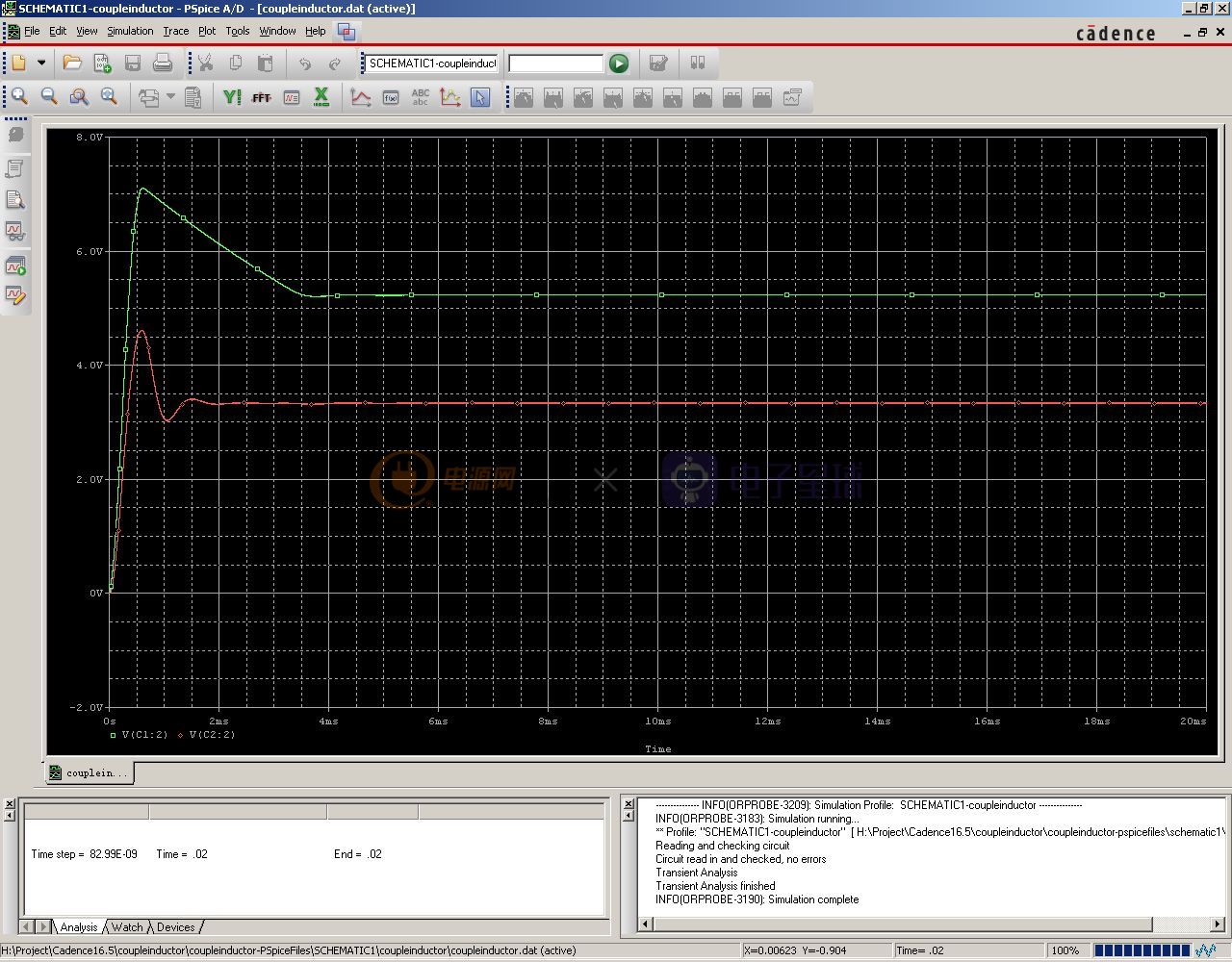
可以看到,即便把5V的输出负载变成20欧,此路输出的电压依然能够保持在一个比较正常的值,而不像独立电感时,电压会飙升到7.5V。这就是耦合电感带来的好处。
很惭愧,我并没有耦合电感输出的正激电源的设计经验。所以,以上只能从基本原理的角度给大家一些原理性分析。具体的设计过程是否合理,我不能确认。欢迎有此类设计经验的朋友参与讨论。另外,实际的工程设计中,元件不是理想化的,耦合电感会存在漏感,而漏感也会影响交叉调整率,所以,实际情况会复杂的多,耦合电感的结构设计会非常重要。


