一、系统框图
系统中的反馈回路可以使用以下众所周知的框图进行建模。
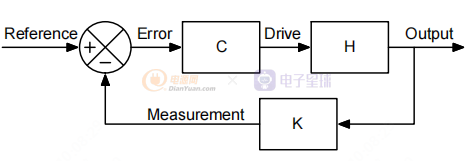图 1. 反馈回路框图
H 块代表要控制的工厂或系统。 它提供由反馈回路控制的输出。K 块在将系统输出与参考值进行比较之前测量和缩放系统输出。 缩放的结果称为测量，比较结果称为误差。 C（用于补偿器）放大比较误差以获得输出中的预期值。 它生成控制设备 H 的驱动信号。
二、系统公式
如果我们写一些描述系统关系的方程，我们得到：
如果我们解决它，我们可以写出输出方程：
通常，在补偿器 C 中，我们构建一个积分器（或在原点放置一个极点）以减少静态输出误差。 在这种情况下，准静态增益（或直流增益）是无限的，所以我们得到：
将（3）代入（2），我们可以得到静态或DC的输出值：
这个方程是众所周知的，并且用于通过电阻分压器来缩放输出值，例如在 TL431 应用中。 使用（1）中的方程组，我们可以推导出另外两个公式。 首先，我们可以提取作为误差函数的测量。 这就像通过排除比较器来打开系统。
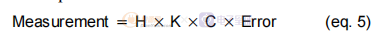
系统开环方程：
其次，我们可以将 Measure 提取为 Reference 的函数。 使用（2），我们得到：
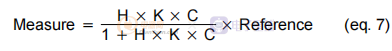
这个公式描述了我们可以称之为 S 的系统闭环方程。
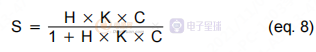
然后我们可以不同地组合这些术语，并获得闭环表达式和开环表达式，反之亦然。
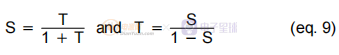
三、稳定性标准
在系统方程（8）中，我们可以清楚地看到，如果分母为零，则 S 是不确定的。 这是系统输出值存在的条件之一。 实际上，如果不满足此条件，系统将变得不稳定（并振荡）或饱和至电源轨之一。
拥有稳定系统的最低要求是：
Nyquist是第一个使用图形方法研究反馈回路稳定性的人，以确定系统是否稳定。 开环传递函数 T(jω) 作为脉动频率 2πf 的函数绘制在虚轴上。 如果该曲线在频率增加时环绕 (-1 + j0) 点，则系统（通过闭合反馈回路制成） 不稳定。 如果不是，显然系统是稳定的。
该奈奎斯特准则为我们提供了以下稳定和不稳定系统的图表。
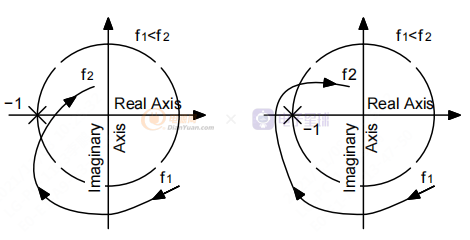图 2. 奈奎斯特准则
为了具有更好的鲁棒性和确保稳定性，定义了两个主要标准。 它们基于开环传递函数图分析。 对于绘图，我们可以使用 Nyquist 、Bode 或 Black-Nichols 图。
相位裕度定义为开环传递函数相位与交叉频率下的 -180° 之间的差值（即，当开环传递函数增益为 1 或 0 dB 时）。
增益裕度定义为开环传递函数增益与 0 dB 增益之间的差值，当开环传递函数相位等于 -180 时。
这给出了以下图表来评估这些标准。
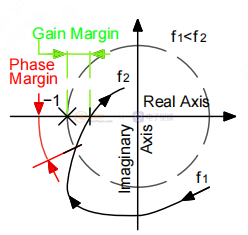图 3. 奈奎斯特图中的边距
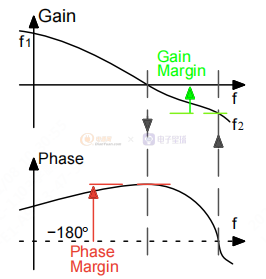
图 4. 波特图中的边距
Black-Nichols 图是测量相位和增益裕度的最简单方法。 一开始，没有与频率的链接会干扰用户，但这是一个简单的测量方法，因为稳定性很重要。
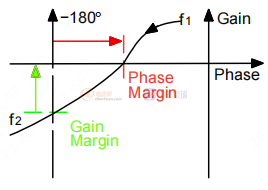图 5. Black-Nichols 图中的边距
Black-Nichols 图的另一个优点是，如果增益发生变化，它只是曲线的向上或向下移动。 当光耦合器的电流传输比 (CTR) 随工作条件变化时，会发生这种类型的偏移。因此，很容易预测下图所示的剩余余量。
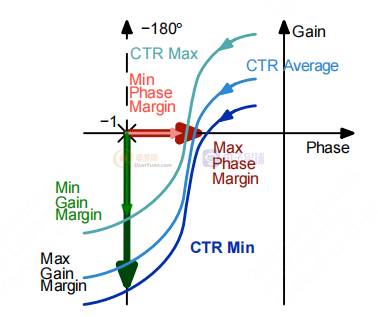图 6. 增益和相位裕度变化与传递函数增益变化