一、原则
当我们没有方程 H 时，就不可能直接使用反馈设计方法。我们可以或需要使用模拟或测量来获得设备（或系统）传递函数。
显而易见的方法是直接测量或模拟设备以对其进行表征。在非线性系统中，设备方程随连续（或直流）工作点而变化。在测量过程中，低频效应，如自热，会影响工作点并修改设备传递函数。在增益非常高的系统中，甚至可以饱和。当这种情况发生时，测量不再是在线性区域中进行，需要采取措施将系统恢复到线性模式。最常用的方法是在闭环中表征设备。反馈将负责设置工作点。在测量过程中，它将补偿低频漂移效应，如自热，并使系统保持在线性区域。
为了在回路闭合时提取开环，我们在反馈回路中注入（或添加）一个小信号。注入的信号会扰乱系统。通过测量效果，我们可以得到开环传递函数。我们获得以下设置。
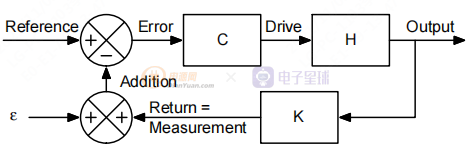图 7. 测量或模拟设置
在上图中，代表注入的信号。 我们将返回信号定义为将添加到注入信号的信号。 加法是那个操作的结果。返回也可以看作是注入信号扰动的结果。 带注入加法器的系统方程如下：
由于我们正在寻找传递函数，我们将使用正弦波信号作为注入信号。 通过改变注入信号的频率，我们可以确定频率响应并绘制传递函数的波特图。
由于参考是直流信号，我们专注于频率响应。 它可以从图片中排除，因为它不包含频率信息。
使用这些假设，我们可以求解（11）中给出的方程以获得输出方程。 然而，这还不是最有趣的。 由于我们已经“打破”了注入加法器的循环，我们可以专注于它周围的信号。 由于 Return 不知何故是注入信号 ε 效应的结果，我们可以求解系统并得到作为 ε 或加法函数的 Return 方程。我们可以很容易地得到：
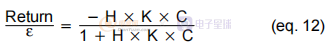
同理可得：
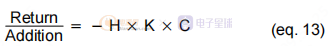
我们可以看到（13）和（12）分别与开环和闭环方程相反。 这是因为从理论上讲，比较器不在图片范围内，而是充当“回路断路器”。 在测量或仿真设置中，注入加法器的作用是在该点“中断”循环，而比较器则保持不变。
二、分析
注入加法器可以放置在循环中的任何位置，等式（13）和（12）仍然有效。有三种简单的方法可以制作一个简单的注入加法器：
1. 与浮动电源串联注入电压。
2. 就像在射频放大器中，单根同轴电缆传输信号并远程传输功率，使用低通和高通滤波器合并注入的交流信号及其直流成分。
3. 使用真正的电压加法器。
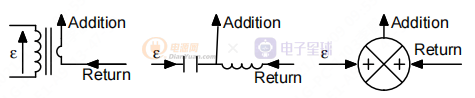图 8. 注入加法器
对于模拟文件中的第一个解决方案，我们只需在要注入的电线中插入一个纯交流电源。 对于实际产品中的测量，最常见的方法是通过变压器操作浮动正弦波发生器以提供电流隔离。
对于模拟文件中的第二个解决方案，我们使用非常大的组件值来形成一个非常低的交叉频率滤波器。 一个 1 kH 电感器将阻止交流内容并对直流内容造成短路。 相反，即使在非常低的频率下，一个 1 kF 的电容器也会阻止直流成分并短路交流成分。 对于测量，由于注入信号频率在数十赫兹到数百赫兹的范围内，因此很难获得足够大的组件，此选项仅适用于仿真目的。
对于第三种解决方案，加法器模块通常在模拟器库中可用。 对于测量，我们可以使用运算放大器和一些电阻来构建具有单位增益的放大器。
三、测量
首先，如果我们要测量系统，我们需要在不影响运行环境的情况下注入信号。 在我们打破环路的那一点，我们必须注意阻抗匹配。 这种说法意味着注入加法器的输入阻抗与断点处的阻抗匹配，而注入加法器的输出阻抗与断点相同 在断点处。
图 9. 阻抗匹配原理
为了简化这些条件，我们可以选择输入阻抗无穷大或输出阻抗为零的断点。
理论上，理想的运算放大器没有输入阻抗（它是开路输入），也没有输出阻抗。
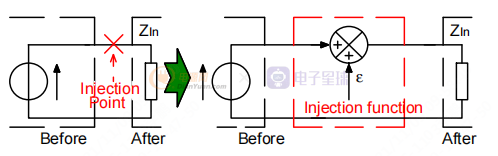图 10. 运算放大器阻抗匹配
如果环路中有运算放大器，则满足此条件。 事实上，运算放大器输出阻抗几乎为零（或低于 1Ω）。 一般情况下，运放输出负载在kΩ范围内。
图 11. 断开运算放大器的环路
在许多情况下，运算放大器输出连接在 PWM 设备内部，因此不可能在该点断开环路。 一种解决方案包括在输出处中断循环。 通常，输出阻抗很低，而测量网络输入阻抗很高。因此，我们可以使用该点，因为它几乎就像一个电压源。 这只会引入与输出与输入阻抗之比成正比的小误差。
图 12. 在输出端断开环路
在仿真中，我们也必须关心阻抗匹配，但一般情况下，放大器输出是可用的。其次，为了确保足够的测量条件，我们必须确保系统保持在线性区域。如果注入信号是正弦波，则所有其他信号（特别是加法和返回）也应该是正弦波。因此，我们需要为 ε 使用一个较小的值。但是，如果调制幅度太小，则不会无法正确观察关键信号，因为它们会淹没在环境中。
在这种情况下，测量是不可能的。因此，调制电平应具有足够的幅度以保持在本底噪声之上。为了简化测量过程，我们可以使用现代示波器提供的一些功能，例如平均、同步检测或高级触发。
在仿真中，随着程序线性化在运行小信号分析之前的电路中，幅度无关紧要，结果不取决于注入信号幅度。在任何情况下，测量或仿真都不应依赖于环路中的注入加法器、注入加法器设置和注入信号幅度。如果动态结果随着调制幅度的变化而变化太大，则表明系统未在其线性区域中运行，可能需要调整设置。
四、结果
根据可用信号，还可以绘制（通过测量或模拟）其他传递函数。 唯一的条件是注入加法器在我们想要绘制的传递函数之外。例如，观察输出与驱动的比率将为您提供工厂传递函数 H。这很明显，这里最困难的一点是访问 驱动信号。如果注入加法器连接到输出（在这种情况下，返回 = 输出），如果我们绘制驱动/加法，我们会得到补偿器乘以比例因子 (-KC) 的相反结果，因为比较器位于 路径内。