在具体分析反馈电路模型之前,我们先来简单探讨一下一个基本知识——电路的传递函数。
什么叫做传递函数呢?通俗的来说,我们把一个系统看作一个黑箱子,黑箱具有输入和输出,而输出和输入会建立某种固定的关系,这个关系可以用一个函数来表达,这个函数可以称之为传递函数。举个最简单的例子,比如用两个相同的电阻串联来分压,我们可以知道分道的电压为输入电压的0.5倍,而且不管输入电压怎么变,0.5的比值都不变。 其实这个0.5就是最简单的传递函数,整个表达式可以写作 输出/输入=0.5,但是实际中我们的电路不可能永远这么简单,当电路更加复杂的时候,我们就需要引入另外一个概念,就是频域。

首先我们来看一个图上的所画的简单的rc电路,对于这样一个rc电容,我们如何来计算输入和输出的关系呢?假设输入是个直流信号,我们可以很简单知道输出是个同等大小的直流信号,那么如果输入不是直流信号,那么输出会是一个什么样的信号?
虽然基本上所有的工程师都知道,这样一个rc电路,其实就是个低通滤波器,它会衰减高频信号,那么到底对什么样的信号会衰减,会衰减多少,我们需要一个可以量化计算的方法,这里就需要用到频域的概念,在频域里面信号都是以正弦波的形式存在的,而正弦波除了有幅度,他还有频率和相位这几个参数,电路里面的元器件阻抗也要以负阻抗的形式存在。比如在频域里面,电阻r还是用r来表达,但是电感l的阻抗是用 s*l来表达电容c的阻抗, s乘以1/c来表达,其中 s=ωj,ω是指的角频率,那么这个角频率和我们熟悉的频率之间的关系是ω=2πf, j就是表示的复数。
这样一来我们可以知道,除了电阻,电感和电容的阻抗会随着频率变化,电感的阻抗会随着频率的增大而增大,而电容则相反。得到了这些元器件的复阻抗表达式之后,我们就可以利用基尔霍夫定理在频域里面计算出简单的rc电路的传递函数,那么我们得到这样一个传递函数 输出/输入=1/(scr+1)。
其实这里的话就是一个以复数形式表达的传递函数,而对于复数来说,它是可以求模,那么膜在实际意义里面其实就是信号的增益,也就是输出信号的有效值和输入信号之间的比值是放大了还是缩小了?放大倍数又是多少?可以用增益来表达。那么复数还可以求角度,也就是我们实际情况意义里面的像,也就是输出的信号的相位减去输入信号的相位得到的相位差。总而言之,复数形式表达了传递函数,既可以准确反映信号幅度的变化,也可以反映信号相位的变化。
那么在这里要注意的是 s这个符号,刚才讲过s=ωj那么其中包含了一个变量,ω就是角频率,也就是说当信号的频率变化的时候,s就是个变量,这个变量会导致传递函数的模和角度会随着频率的变化而变化。如果我们把幅值和频率的关系图描绘出来,就可以得到个增益曲线,把相位和频率的关系图描绘出来,可以得到一个相位曲线,那么这几个曲线我们称之为波特图。
在这里我们留个思考题,假如说我们有一个两级rc滤波器,那么这个滤波器的传递函函数会是怎么样的?大家可以去推导一下。
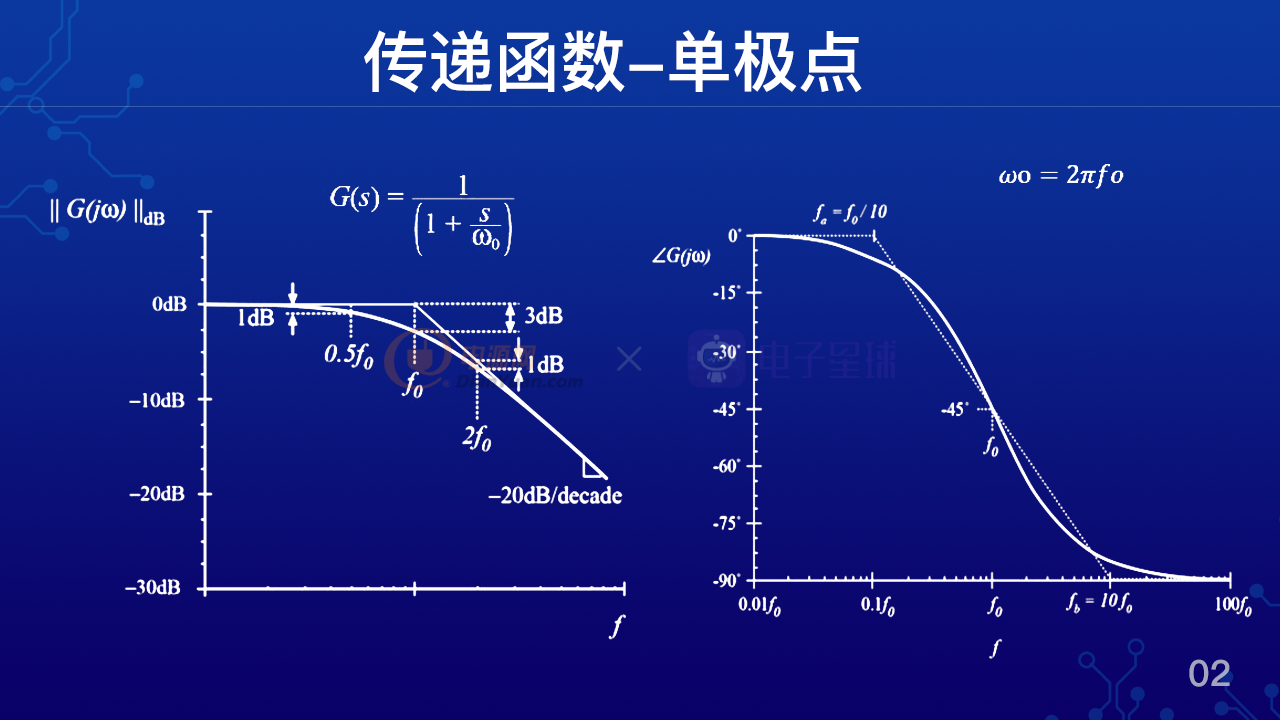
在刚才我们已经求出了rc滤波器的传递函数,但是这样的传递函数表达了什么样的物理意义?如果单从公式来看很难理解,但是如果我们把这个函数求模,求出来的模再做对数运算,再乘以20,也就是说把它转化成分贝,那么在以频率为横坐标,分贝为纵坐标就可以得到一个增益的波特图,也就是左边这个曲线。
那么我们看曲线可以得知增益会随着频率的增加逐渐降低,并且在f0这个频率点降低了三个db,那么我们称之为 f0频率点为转折频率点。最后的话我们可以看到争议会议20db10倍频的斜率下降,对于这样特性的函数,我们称之为单极点特性,极点的位置就是转折频率点,就是我们刚才所说的f0。
那么如何计算这个f0的值,我们可以先把传递函数写成标准模式,就是我们图上所示的G(s)=1/(1+s/ω0),那么其中ω0就是极点的位置。如果我们把刚才rt滤波器的传递函数也写成这样的标准模式,那么就可以写成 Vout/Vin= 1÷(1+ s)÷1/rc,那么这里也可以得到ω0=1/rc,那么转化成f0,就是f0=2π 1/rc,也就是说其实rc滤波器表现出来就是单极点特性,而这个极点的位置在2π 1/rc。
对于增益图,通常为了简化分析,理论上可以用渐进性,也就是图中的折线来代替,折线的转折点就是转折频率点,采用折线来近似,非常适合早期没有计算机的时代,可以大大简化波特图的分析和理解。但是现在计算机如此的发达,我还是建议大家利用计算机来汇出完整的增益曲线。
同时我们知道复数表达的函数,还有相位角度的问题,那么右图就是单极点传递函数的相位曲线。
我们可以看到在转折频率点相位之后正好45度,但是相位其实从远远小于转折频率的地方就开始滞后了,一直到无穷大频率处,最后总共滞后90度。换个说法,就是一个单极点会带来90度的相位之后,那么如果为了简化分析,我们也可以做一个近似,通常就认为在1/10转折频率点,相位就开始滞后,到转折频率点,正好滞后45度,再到10倍的转折频率点,认为它已经滞后了90度。就这样我们把具有单极点特性的传递函数的波特图描绘了出来。
从增益曲线上我们可以看到,增益在频率接近0的地方为0db,也就是一这意味着在低频段输出接近输入,但是随着频率的增加,增益开始下降,呈现出明显小于一的特性,这就意味着信号被衰竭了,验证了低通滤波器的特性。那么从相位曲线也可以看到,在低频段相位滞后很少,但随着频率的增加,最终会滞后90度。那么这个就是整个低通滤波器表现出来的特性,我们也可以称之为单指点特性。
除了表现为单极点特性的传递函数之外,我们再来看一下其他类型的传递函数工。比方说我们把这个单极点的传递函数做一个倒数运算,就可以得到这样一个表达式,就是G(s)=(1+s/ω0) 。如果我们把这个表达是求膜求相位,就可以把波特图描绘出来。
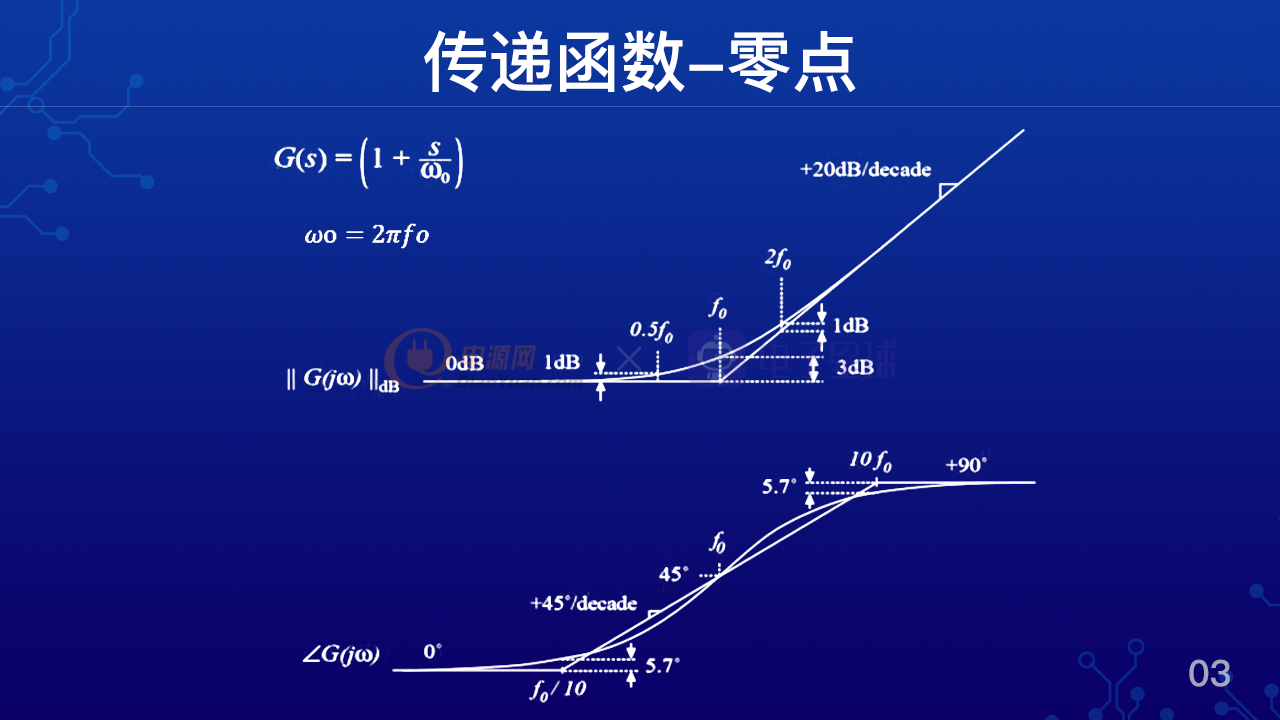
可以看到如图所示的两个曲线。我们先看上面的增益曲线,从这个增益曲线可以看到增益从0db 开始,然后到接近f 0的地方开始上升,到f 0处上升了3个db,最后他会以20db每十倍频的斜率上升。我们马上就会意识到这个增益曲线其实和极点正好相反,那么我们称之为零点,这个零点的位置就是f 0,如果以角频率点表达,就是ω0。那么再看下面的相位曲线呢,可以近似的认为从十分之一的转折频率开始超前,在零点的位置超前45度,到10倍转折频率处超前90度。
所以说零点的特性和极点是完全相反的。这就是我们为什么会经常听到说用一个零点去补偿一个极点的说法。因为他们两个是对偶的是互补的,是可以互相抵消的。

除了极点和零点,那么我们再来看另外一个表达式,G(s)=1-s/ω0 。那么和刚才那个零点的表达是不同的是,0点是1+s/ω0,这里是-s/ω0。
这个表达式呢就是表示了一个右半平面0点。这个右半平面零点在波特图中的表现形式为增益随着频率上升,但是相位却是随着频率滞后。也就是说它的增益曲线和零点相同,但是相位曲线却和极点相同。
那么在什么样的系统里会碰到右半平面零点呢,就在ccm 模式的boost ,或者Buck/Boost或者反激这些拓扑中会碰到这个右半平面0点。
那么右半平面零点在电源系统中具体表现是什么呢?比如在boost 中,如果负载突然变重,输出电压下跌环路会加大占空比。但这个时候整流管的的占空比一减力就会相应变小。
但此时电感电流却没有立即升起来,会导致不适的整流管输出平均电流反而减小,从而进一步加剧输出电压下跌。这就是右半平面零点的物理特性。理论上来说,右半平面0点可以用右半平面极点来补偿。
但是事实上在我们的开关电源系统中,我们没有办法在补偿电路中构建这样一个右半平面极点。所以这个右半平面零点我们根本没有办法补偿。这也就意味着具有右半平面零点的拓扑在环路上具有严重的局限性。
在了解了一些基础传递函数的增益特性和相位特性之后,我们来看一下,如果把这些基础函数乘起来,就可以得到更加复杂的传递函数。
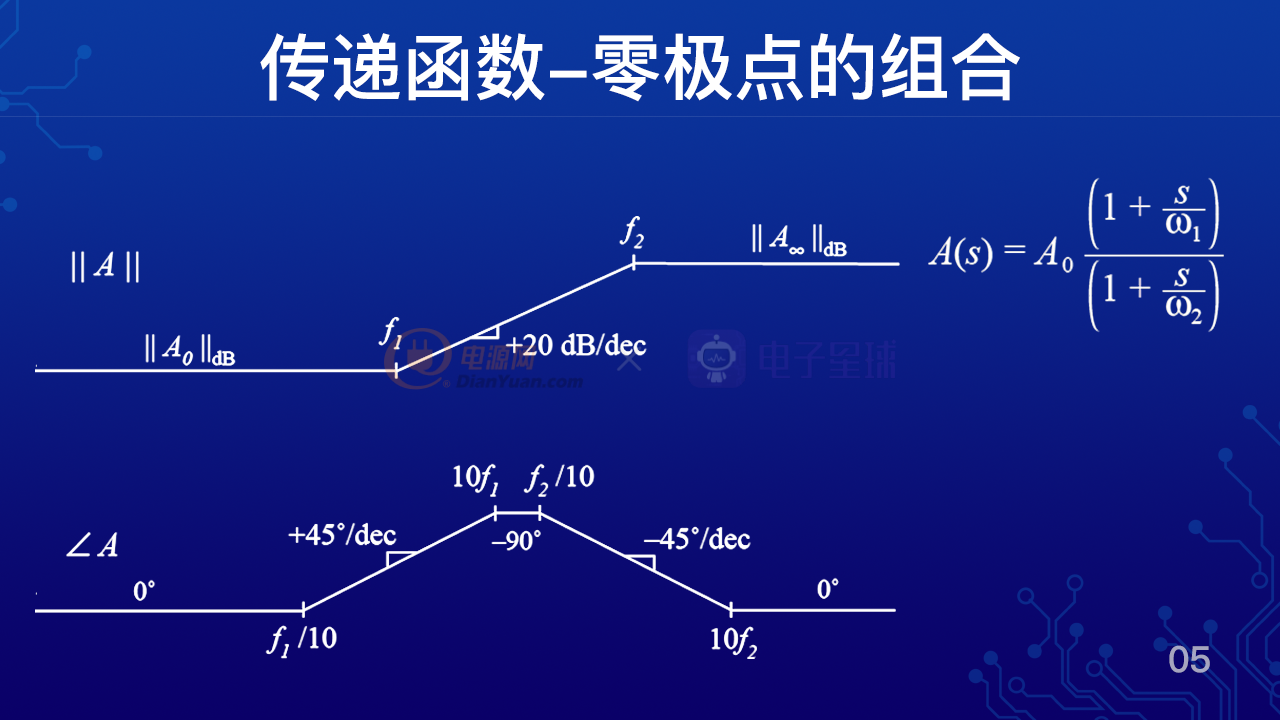
如图所示,我们可以把一个极点和一个零点的传递函数相乘,可以得到这么一个表达式。
A(s)=A0*(1+s/ω1)÷(1+s/ω2),这个表达式里面包含了一个极点和一个零点,A0是直流增益,ω1为一个零点,ω2为一个极点。
如果ω1=ω2,我们可以得到这个函数会变成极其简单的比例函数,就是A(s)=A0。这种函数的增益曲线和相位曲线都会变成一条直线,也就是我们常说的零极点互相补偿,互相抵消。
那么如果ω1≠ω2,假如ω1<ω2,我们就可以得到如图所示的波特图。
首先看上面的增益曲线,我们可以发现随着频率的增加,我们先碰到一个零点,ω1或者f1过了零点之后,争议以20db每10倍频的斜率上升,等到了ω2或者f2这个频率点,我们又碰到了一个极点,增益就不再上升,后面的增益曲线就变平了。
那么再看一下下面的相位曲线,相位在十分之一ω1处开始超前,到10倍的ω1处超前了90度,在十分之一ω2处开始滞后,最终在10倍ω2处滞后的90度,这样一个超前一个滞后,他们互相抵消就可以得到高频处的相位和低频处的相位是相同的。也就是说最后总共的相位超前或者滞后只有0度。
但是在这里我们要注意一下,这里有个前提假设,假设10倍的ω1要比十分之一的ω2还要小,如果10倍的ω1是要大于十分之一的ω2,我们就会发现中间拱起来的相位超前不会达到90度,因为它还没有达到90度,就会被ω2这个极点影响,从而转向开始下降。
所以大家可以想象一下,这种情况下,如果ω1和ω2开始靠近,增益曲线和相位曲线又会怎么变化呢?那么再当ω2小于ω1的时候又会怎么样?大家可以去思考一下。
除了上述所讲的单极点、单零点以及零极点的组合之外,在开关电源系统里面,我们还会碰到更加复杂的传递函数,那就是复合双极点。比如常见的lc滤波器的传递函数,就是一个典型的复合双极点。复合双极点和单纯的两个极点相乘不同,复合双极点有时候是无法解析出三个节点来的,我们不能简单的把它认为是两个极点的组合,必须统一起来分析。
复合双极点标准表达式为:

其中ω0为转折频率,Q为品质因素,简单的来讲,双极点的增益曲线表现为过了转折频率之后,以40db每10倍频的斜率下降,这种斜率是单极点的两倍。

但是复合双极点还有一个特性,那就是Q值。当Q值很大的时候,就是左图最上面的曲线,表现为在转折频率点增益会变得很大。那么随着Q值的降低,转折频率点的增益也逐渐降低,越往下面的曲线表现为Q值逐渐降低。 右边是相位曲线,我们可以看到当Q值大的时候,相位之后的非常快,如同跳水一样,在很窄的频率范围内就可以实现180度的相位滞后,但是Q值低的时候缓和很多。
那么符合双击点到底能不能解析为两个单极点的组合?其实当Q小于等于0.5的时候,我们可以把复合双极点解析为两个单极点的组合。比方说当Q=0.5的时候,我们可以把复合双极点解析为两个单极点,这个时候两个单极点在同一个位置,就是ω0。事实上这种复合双极点在我们开关电源系统里面是很常见的。
刚才我们讲到复合双极点是个比较复杂的表现形式,但是我们知道当Q小于等于零0.5的时候,可以解析为两个单极点组合。

刚才已经讲了,Q=0.5的时候,可以解救一对位置相同的极点。那么Q<0.5呢,在早期计算机不是很发达的时候,为了简化理解,我们通常会做一些近似,那就是当Q明显小于0.5的时候,可以把这对复合双极点分解为两个单极点,一个为Q乘以ω0,另外一个有1/Q乘以ω0,这样就很容易理解和计算。
当然实际上现在随着计算机技术的发展,我们已经很少在应用的时候采用手动记账,而是采用计算机软件进行计算,比如Mathcad的excel等工具就可以。所以这种近似的方法已经不是那么重要了。但是对于学习的人来讲,还是有一定的意义。


