前面讲了一些基本的传递函数,但是这些都是开环电路的传递函数,我们现在来阐述一下基本的闭环系统的传递函数。
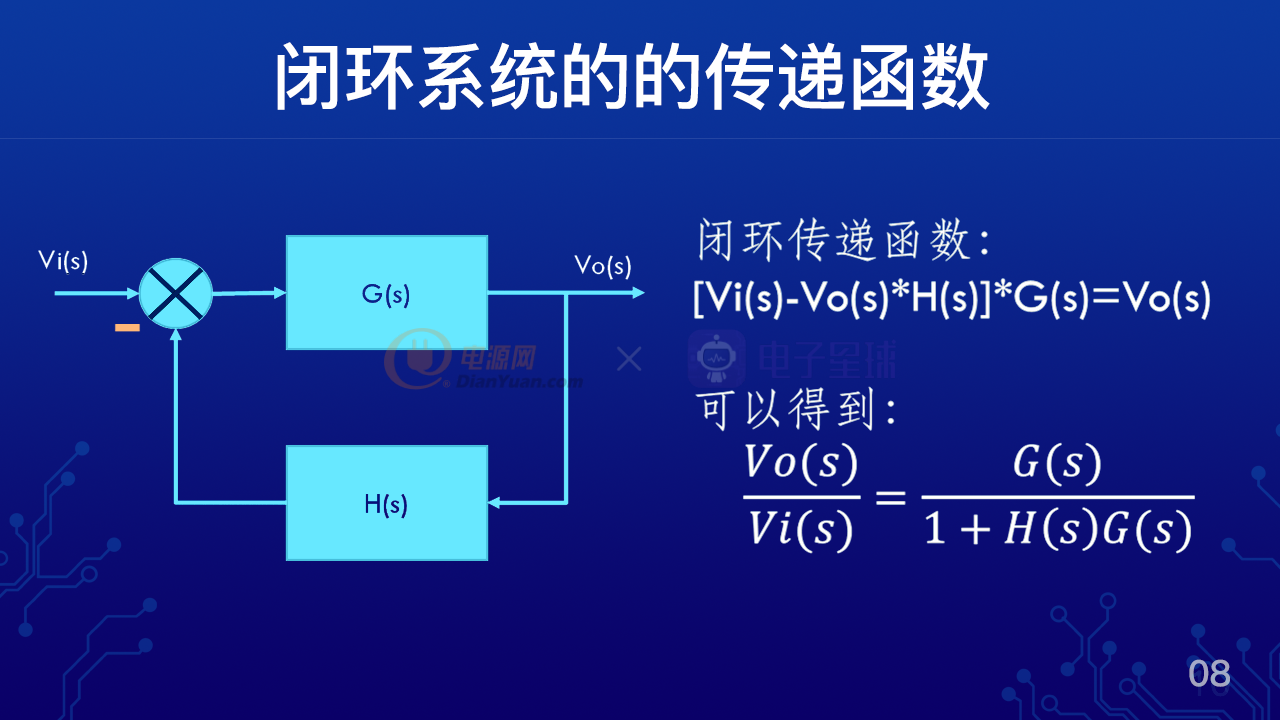
左边框图表示了一个带有负反馈的闭环系统,其中Vi(s)为输入信号,Vo(s)为输出信号,G(s)为前项的传递函数,H(s)反馈传递函数,那么我们就可以得到这样一个等式,[Vi(s)-Vo(s)*H(s)]*G(s)=Vo(s),这里的Vo(s)*H(s)为反馈过来的信号,那么把这个等式经过变化之后就可以得到Vo(s)/Vi(s)= G(s)/[1+H(s)G(s)],这样的表达方式我们称之为标准的闭环传递函数。其中H(s)*G(s)为开环传递函数,那么这样的闭环传递函数表达了输出Vo和输入Vi的一种关系函数。
从闭环传递函数,我们同时可以得到一个线索,如果H(s)*G(s)也就是开环传递函数,正好等于-1的时候,那么 Vo/Vi就会变得无穷大,也就是说这个时候系统会产生自激震荡,那么在复数里面-1表示什么呢?它表示的就是增益为1,或者说0db相位180度。由此我们可以得出什么结论呢?在这样一个负反馈系统里面,如果开环传递函数的增益等于0,或者说0db,同时相移为180度的时候,整个系统就会出现自激震荡。所以我们在设计闭环反馈系统的时候,要避免出现这样的情况。
那么这里要强调一点,有的时候我们会把负的H(s)乘以G(s)嘴开环传递函数,也就是说把反馈里面的减号算在开环传递函数里面,如果这样的话,计算出来的结果要在开环传递函数等于1的时候,系统会产生自激震荡。那么传递函数等于1,就表示着增益为0db,相移为360度。事实上我们在计算电源补偿环节的时候,经常有人会搞错负号的计算,导致两种计算的相位相差了180度。
刚才我们说到可以根据开环的传递函数来判断什么时候会产生自激震荡。为了避免这种自激震荡,我们就需要避免开环传递函数等于-1的情况,意味着不能让增益等于0db,相位等于180度,这两种条件同时出现,这样才能保证系统的稳定性。
那么我们怎么来判断反馈系统有足够的稳定性呢?有一种非常简单的办法,就是描绘波特图来判定。
如何描绘波特图呢? 首先我们要把开环传递函数就是H(s)乘以G(s)的函数公式写出来,这个公式写出来之后一定是一个复数函数,然后对这个复数函数求模,把求出来的模以横轴为频率,纵轴为增益的形式描绘出来。其次,可以对负数函数求角度,也就是相位,把相位以同样的方式描绘出来,这样就形成了开放函数的波特图。
波特图里面包含了增益曲线和相位曲线,那么如图中所示,图中的蓝色曲线为增益曲线,红色曲线为相位曲线,从这个波特图中我们就可以得到三个重要的参数。
第一个就是相位余量。什么是相位余量?就是当增益穿过0db的时候,相位离180度还有多少余量。这里还要强调一下,如果开环传递函数是负的H(s)乘以G(s)那么就是离360度或者0度还有多少余量称为相位余量。通常我们认为相位余量大于45度,是足够维持系统稳定性的。
第二个就是增益余量。当开环传递函数相位达到180度或者0度的时候,增益离0db的余量叫做增益余量。我们认为小于-6db就可以维持系统稳定。
这两个余量都是为了避免系统产生自激震荡而保留的余量。但是在很多情况下,有些客户会要求我们设计的电源系统相位余量达到60度,增益余量达到-10db,这些更高的要求。
第三个参数就是带宽或者说穿越频率,在开关电源系统里面,我们希望带宽越宽越好,带宽宽意味着动态响应更容易做好,但实际上电源系统的带宽是受到约束的。一般情况下,电源的带宽受开关频率的限制,通常我们会把带宽设计在1/5~1/6开关频率以下,但是如果这个电源系统有右半平面零点,那么带宽就会设置在1/3右半平面零点以下。
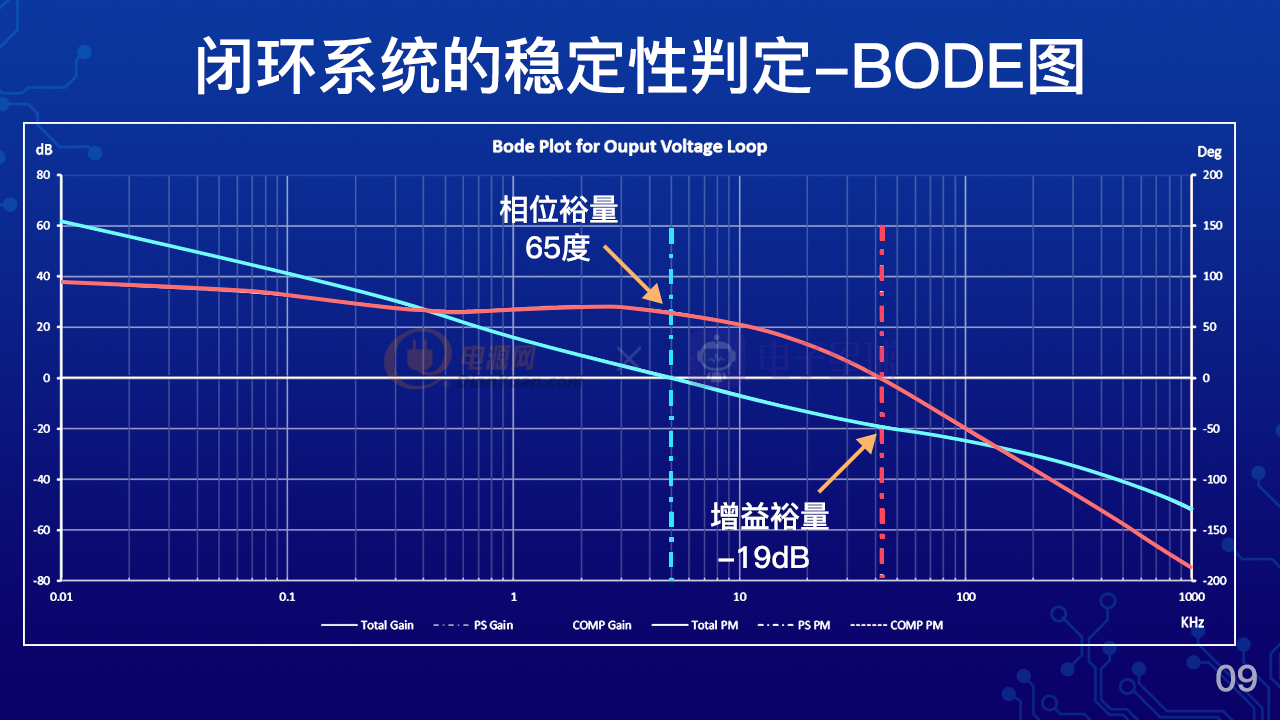
在这张图里面我们可以看到这个波特图的相位余量为65度,增益余量为-19db,而带宽大概在5k左右,在我们实际设计中不可能把三个参数都设置的最优,因为他们都有互相牵制的作用,所以这三个参数一定是全盘考虑折中之后的结果。
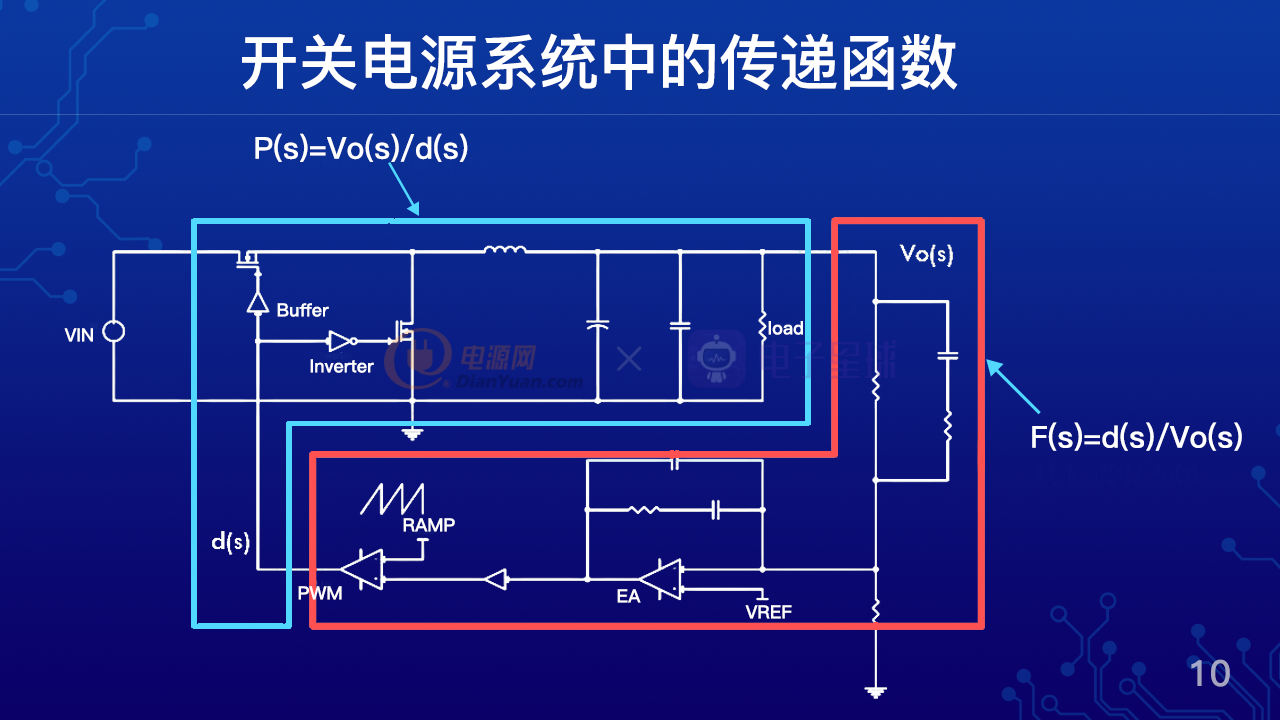
在开关电源系统里面,我们通常把整个开关函数分成两个大的环节,比如图中所示的电压型buck电路,我们把红框里面的电路做一个环节,这个环节所表达的函数F(s)=d(s)/Vo(s),这个表达式的物理意义就是当Vo产生变化的时候,占空比会怎么变化。篮筐里面的电路作为另外一个环节,那就是P(s)=Vo(s)/d(s),它表达了当占空比变化的时候,Vo又会怎样变化。那么F(s)乘以P(s)就形成了该电源的开环传递函数。
接下来我们就要去做的就是,第一步,把F(s)和P(s)的传递函数写出来,然后把两个函数相乘,最后形成一个总的开环传递函数。第二步,把这总的开环传递函数的模和相位求出来,并且以波特图的形式把曲线描绘出来。第三步,根据波特图来判断其稳定性。
我们可以说第一步是最关键的一步,也是最难的一步,我们来看一下电路图,为什么我们要把它分成两个环节。一个是红框里面的电路,一个是篮筐里面的电路。因为我们可以看到红框里面的电路是完全线性的电路,对线性电路来说,我们只要学过电路原理,都能轻松的写出传递函数。但是篮筐里面电路却是包含了开关电路,这是个非常典型的非线性电路,对于非线性电路理论上是写不出传递函数的。
这里来介绍一下什么是线性电路呢?就是全由线性元器件组成的电路称之为线性电路。比方说我们常用的电阻,电容和电感,以及运算放大器等就是线性元件,因为他们的参数并不会随着外界条件的改变而改变。比方说电感的感量,理论上是不会随着电感电流变化,又比如说电容的容量也不会随着电容上的电压变化,这样的元器件称之为线性元件。但是什么又是非线性元件呢?比如mos管,mos管工作在开关状态的时候,它是受门极电压控制的,当门极电压是高电平的时候,导通mos管可以等效为一个很小的电阻,但是当门极电压是低电平时,mos管关断,它又可以等效为开路模式。就是这种参数受其他条件控制的元器件称之为非线性器件,包含了非线性器件的电路,就是非线性电路。
当然我们实际应用的电感和电容多多少少有点非线性特性,比如电感的感量实际上会随着电感电流增大而下降,而某些电容的容值也会随着电容上的电压增大而减小。但是我们在理论分析的时候,还是会把这些元器件当做线性元件来分析。
早在上个世纪开关电源的稳定性分析一直困扰着电源工程师,因为大家都知道开关电源是非线性系统,无法写出线性电路中的传递函数,而非线性电路理论又是大家不熟悉的知识,所以基本上电源的稳定性只能靠测试、经验等方式来解决,直到几位美国的大学教授开辟了一个新的路径,就是把非线性电路线性化,我们现在常说的状态空间平均法。状态空间平均法的要义就是把离散的周期信号平均化,然后近似为连续信号。
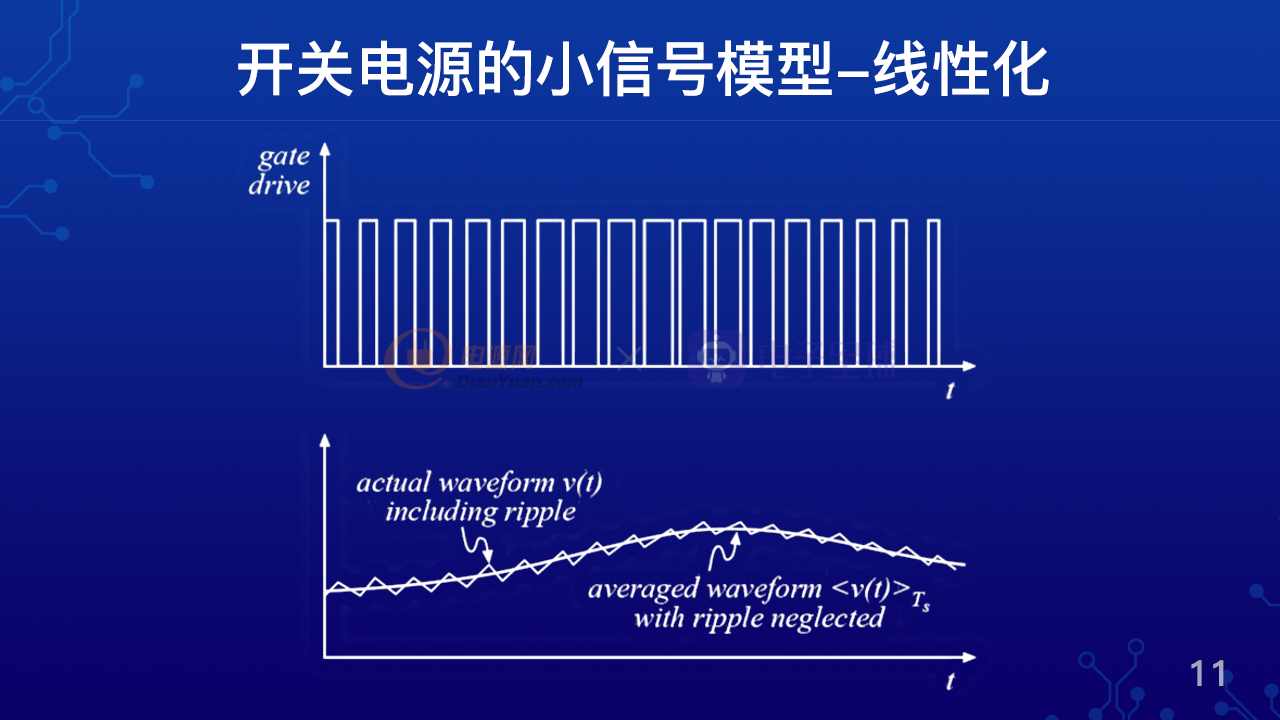
比如上图的脉冲波,为一串占空比不断变化的脉冲,这就是一个离散的信号。如果我们把这些信号在一个周期内做平均,或者说我们来个低通滤波器,滤掉高频信号,我们就可以得到一个带有开关纹波的连续波动信号。再次把开关频率的纹波抹掉,我们就可以得到一个连续光滑的波动曲线。这样我们就把脉冲电压信号平均等效为下图中的连续信号。基于这样的思路,就可以把开关电源中的一些周期开关信号平均为连续信号,并且把开关电路等效为一些线性电路。
基于这种近似等效的方法,我们就可以建立开关电源的交流小信号模型。为什么叫交流小信号模型呢?因为这种模型是建立在直流工作点上的交流模型,而且这个模型只有在传递足够小的信号前提下,才能保证准确性,但是这种模型对开关电源的环路分析具有非常重大的意义。这种模型由于做了平均化,事实上只有在低频信号下才是准确的。如果当信号频率开始接近脉冲信号频率的时候,它的准确度就会大大降低。比如下图中的连续信号,包含了低频的劳动和脉冲频率的波动,平均法建立的模型对低频劳动来说是准确的,但是对脉冲频率的劳动是不准确的。
在我们实际应用中,通常认为信号频率低于开关频率的1/3,可以认为是比较准确的,低于开关频率的1/10,这种模型可以认为是非常准确。那么这个状态空间平均法虽然是采用了近似的方式把开关电路线性化了,有着很多的局限性,可是他的理论简单易懂,方法直接有效。所以到目前为止,依然是最受欢迎的分析方法。
虽然利用状态空间平均法推导小信号模型,在学术上被认为是相对简单的方法,但是实际上它并没有那么简单,还是需要繁琐的公式推导,这就需要相当的数学功底。虽然这些知识在我们一些大学教科书上已经被详细的阐述了,但是很多工程师还是无法准确地推导出小信号模型。不过幸好我们电源所用的大多数拓扑都是被研究了一次又一次,所以基本上常见的拓扑小信号模型都已经被推导过了,我们只要直接拿来用就可以了。
这里我们就来看一下三个基本拓扑Buck、Boost、Buck-Boost。

在电压模式下的小信号模型,这边采用一个统一的公式来表达三个拓扑的小信号模型, 那就是:
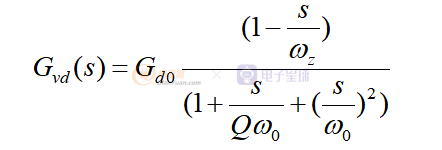
在这Gvd(s)表达了 V o的变化除以占空比的变化。也就是说当占空比在某个直流工作点的基础上,出现了正弦波的交流劳动,那么这个劳动最后会传递到输出,这个传递函数就是表达了输出和占空比之间的关系。
仔细看一下这个传递函数它包含了三个要素,首先是直流增益Gd0,还有是一个右半平面零点ωz和一对复合双极点ω0。
具体来先看Buck电路,Buck电路的直流增益为V/D,其中的V表示为输出电压,那么V/D实际上就是输入电压,所以我们可以说Buck电路的直流增益就是输入电压。其次为复合双极点的位置,这个双极点的位置在:

这里的R为负载电阻,那么理论上来说当空载的时候,也就是R为无穷大的时候,Q值应该也是无穷大。但是我们实际在测试的时候,即便是空载Buck电路的Q值也没有那么的大,那是因为在实际中电感的直流电阻,mos管的导通电阻都会降低Q值,只不过在理论分析的时候没有把它们考虑进去。
最后一个参数就是右半平面零点ωz,事实上Buck电路是没有右半平面零点的,所以这里就是无穷大。
表的下面两行同样列出了Boost和Buck-Boost 4个参数,最主要的不同是Buck没有右半平面零点,而Boost和Buck-Boost有零点。
我们前面也讲了,右半平面零点是无法补偿的,所以Boost和Buck-Boost的环路带宽必须低于右半平面零点。而在实际上为了可靠性,一般会把带宽设计在低于1/3的右半平面零点。如果以Boost为例,我们可以看到占空比越大,负载越重,电感越大,那么右半平面零点的频率越低,所以在设计Boost的时候,为了避免右半平面零点频率过低,电感量必须尽量取小。
当然这里的模型是在连续模式下推导出来的,如果是在DCM也就是在断续模式下传递函数就会有很大的不同。最大的变化就是Boost和Buck-Boost的右半平面零点就不存在了。
除了电压型控制之外,最受欢迎的控制方式就是电流型控制。电流型控制里面比较常用的是峰值电流和谷底电流控制。和电压型不同的是电流型控制常规模型里面并没有lc形成的复合双极点,取而代之的是两个分开的极点,一个在低频处,另外一个在高频处。因为一般情况下高频极点远远高于环路带宽,所以可以忽略掉。为了简化计算,我们只有可以用一个一阶系统的传递函数来表达电流型控制,那么它表达公式为:
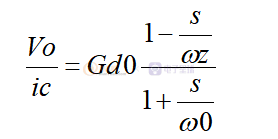
这里的ic表示为受控电流,也就是电感电流的劳动。这个传递函数表达了什么呢?当电感电流出现扰动,最后传递到输出电压的劳动是什么样的。

和电压模式一样,它也包含了三个基本参数,一个就是直流增益Gd0,一个就是右半平面零点ωz,另外就是一个单极点ω0。
以Boost为例,我们可以看到直流增益Gd0为:
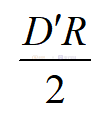
这里的D'=1-D。那么单极点的位置为2/RC,右半平面零点的位置依然为和电压型控制一样为:
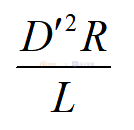
我们可以看到这个传递函数里面只有一个极点,但是在实际应用的时候,电流型控制通常是要加斜率补偿,加了斜率补偿之后,高频极点的位置就会往低频段挪,那样有时候我们就不能忽略掉这个极点,这个时候我们就需要更为精确的数学模型,如果大家对更为精确的数学模型感兴趣的话,可以参考一些文献,甚至有些文献推导出来具有三个起点的精确模型。
那么最后这里再强调一下,对于Boost和Buck-Boost电流型控制并不能消除它们的右半平面零点。
刚才的小信号模型为了简化公式推导,都没有考虑输出电容的ESR,但是在实际应用中,电容或多或少存在ESR,特别是电解电容的ESR更不能忽视。所以我们在计算模型的时候还是要把ESR考虑进去。这里来讲一下电容ESR对环路带来的影响。
首先如果输出只有一个电容,那么电容的ESR会给环路带来一个零点,零点的位置就是ωz=1/RC,或者说 Sz=2π*1/RC,这里的R就是电容ESR。
但是如果有多个电容并联,那么多个电容并联会给我们计算带来很大的麻烦。很多人喜欢把多个电容等效为一个电容,但实际上只有多个相同的电容才能等效为一个电容,如果多个不同的电容并联,不能简单的等效。
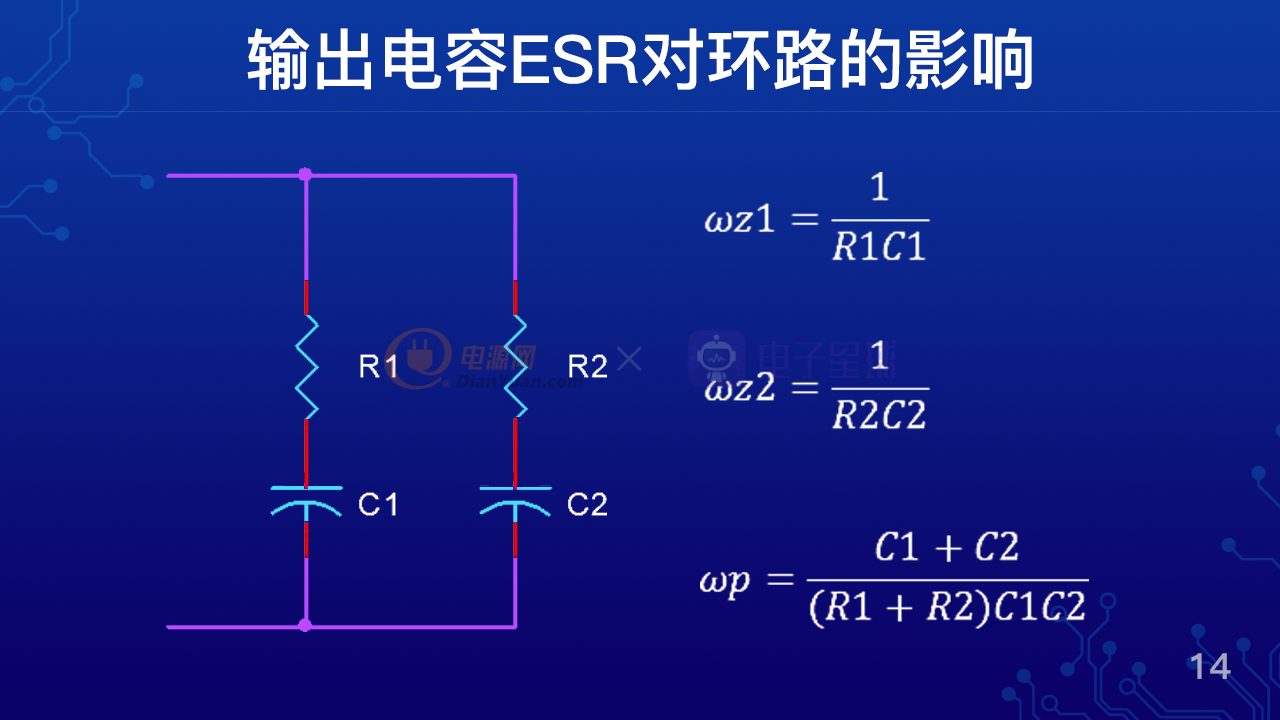
我们来看一下一个两个电容并联的例子,C1和C2并联分别有两个ESR,R1和R2。那么我们可以推导出实际上两个电容并联会给环路带来两个零点和一个极点,分别是ωz1=1/R1C1,ωz2=1/R2C2,ωp=(C1+C2)/(R1+R2)C1C2。这里ωz1和ωz2是两个零点,ωp是一个极点。那么我们可以看出来,只有当C1=C2的时候,并且R1也等于R2的时候,那么其中一个零点就可以把极点抵消掉,这样的话我们就才可以等效为一个电容,可以认为它带来了一个零点。
如果是更多不同的电容并联,那么情况会变得更复杂。所以有时候电容也是我们实际情况和理论有所差异的一个重要原因。


