环路设计和稳定性测试是电力工程师的重要任务。电源,无论是开关模式还是线性模式,都应设计为具有快速瞬态响应和足够的稳定性裕度。不稳定或勉强稳定的电源可能会振荡并导致纹波、电压、电流和热应力增加,并可能损坏电源及其关键负载设备。
奈奎斯特图和奈奎斯特准则
为了评估线性负反馈回路系统的稳定性,一个基本的原始概念是使用奈奎斯特图的奈奎斯特准则。它以贝尔电话实验室的工程师 Harry Nyquist 的名字命名,他在 1932 年发表了一篇关于反馈放大器稳定性的经典论文。他的 Nyquist 稳定性判据现在可以在所有关于反馈控制理论的教科书中找到。
假设反馈系统开环增益传递函数为 T(s),其奈奎斯特图是 T(s) 在 Re(T(s)) 和 IM(T (s)),因为频率 ɯ 作为从 0 到无穷大的参数被扫描。该图可以使用极坐标来描述,其中环的幅度是径向坐标,传递函数的相位是从点 (0, 0) 开始的相应角坐标。通过查看该图上 (-1, 0) 点的包围数来确定循环稳定性。对于典型的模拟反馈环路电源,其开环传递函数通常是稳定的(即,没有 RHP)。在这种情况下,如果随着频率的增加,T(jɯ) 图没有顺时针环绕 (-1, 0) 点,则闭环系统是稳定的,如图 1 所示。

图 1. 稳定负反馈线性系统(电源)的典型奈奎斯特图。
为了保持一定的稳定性,重要的是使 T(jɯ) 图远离临界 (-1, 0) 点。因此,使用 Nyquist 准则和图,电源反馈系统稳定性裕度由 T(jɯ) 图与 (-1, 0) 点的距离决定。严格来说,应该使用 (-1, 0) 点到 T(jɯ) 图之间的最小距离来量化稳定裕度,如图 2 中的值 dm 所表示的。但是,为了简化频域的任务分析(使用波特图),相位裕度 (PM) 定义为 T(jɯ) 图与单位圆相交点的相应相位角 (|T(jɯ)| = 1,或 0 dB),增益裕度 (GM) 由 |T(jɯ)| 确定 值,其中 T(jɯ) 图与实轴相交(即相位 = –180°),如图 2 所示。
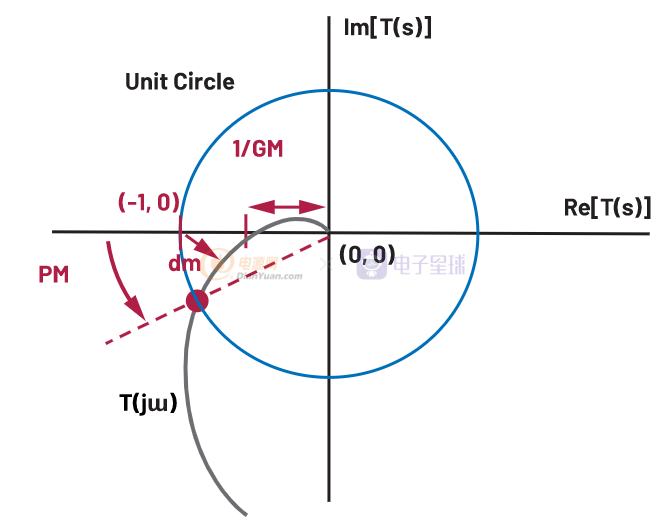
图 2. 奈奎斯特图上的稳定性裕度(相位裕度 (PM) 和增益裕度 (GM))
波特图和稳定性准则
尽管奈奎斯特图提供了反馈系统的准确稳定性标准,但它并没有直观地显示 T(jɯ) 图上的频率值。将此图用于传递函数分析和频域中具有极点和零点的设计并不容易。1930 年代,贝尔实验室的另一位工程师 Hendrik Wade Bode 设计了一种简单的方法来绘制增益和相移图。它们被称为一对波特图,包括相应的增益图和相位图作为频率的函数。以更直观的方式,可以用一对波特图重新绘制一个奈奎斯特图,如图 3 所示。波特幅度图是函数 |T(s = jɯ)| 的图。频率值 ɯ = 2πf。这里,频率的水平 x 轴是对数的。幅度(增益)以分贝为单位给出——也就是说,幅度值 |T| 绘制在 20log10|T| 的轴上。波特相位图是频率值 ɯ 的传递函数 arg(T(s = jɯ)) 的相位图,通常以度数表示。相位值绘制在线性垂直轴上。使用波特图,增益图达到 0 dB(x 轴)的频率定义为闭环带宽 f系统的BW。这与 T(jɯ) Nyquist 图穿过单位圆的点相同。因此,在 f BW处,相位图与 –180° 之间的相位差是 Nyquist 图中所示的相位稳定性裕度 (PM),即 f BW处的 PM = 180 + arg(T(jɯ)) 。请注意,PM ≤ 0 表示系统不稳定。随着频率的增加,供电相位可能会进一步减少。在相位达到 –180° 的点处,与 T(jɯ) Nyquist 图与 Re 轴相交的点相同,其中增益裕量 (GM) 由 1/|T(jɯ)| 定义。总之,Bode 稳定性准则是在 Bode 图中表示的简化 Nyquist 准则。

图 3. 一个典型的稳定系统:奈奎斯特图到波特图以及相应的带宽、相位裕度 (PM) 和增益裕度 (GM)。
例如,图 4 显示了一个典型的不稳定系统及其奈奎斯特图和相应的波特图。在其奈奎斯特图中,随着频率的增加,循环 T(jɯ) 轨迹顺时针环绕 (-1, 0) 点。该图甚至在 |T(jw)| 之前就与 x 轴相交。幅度(即到 (0, 0) 点的距离)下降到 1。T(jɯ) 图与单位圆相交,相位角为负。相应地,在其波特图上,相位图达到 –180°,而增益图仍大于 0 dB。在交叉频率 f BW处,相位值低于 –180°。从波特图中,很容易看出它是一个 PM < 0° 的不稳定系统。

图 4. 一个典型的不稳定系统 Nyquist 图及其对应的 Bode 图
波特图的另一个主要好处是传递函数及其极点和零点的非常明显的表示,以及它们的精确频率位置以及对增益和相位图的影响。这使得回路补偿设计成为标准的工程过程。
最后,虽然波特图增益和相位裕度是经典的稳健性度量,已在控制系统设计中使用了很长时间,但请注意,如果存在多个点(频率),稳定性裕度的波特图解释可能不正确或不准确。 Nyquist 图穿过或接近单位圆(即,Bode 增益图穿过 0 dB)。例如,图 5 显示了一个在波特图上具有良好相位和增益裕度的系统示例。然而,奈奎斯特图显示它非常接近 (-1, 0) 点,具有不稳定的风险。在此示例中,系统不稳健。因此,即使在波特图上,重要的是要查看整个图,而不是只关注 PM(在 f BW处)和 GM 的两个点。
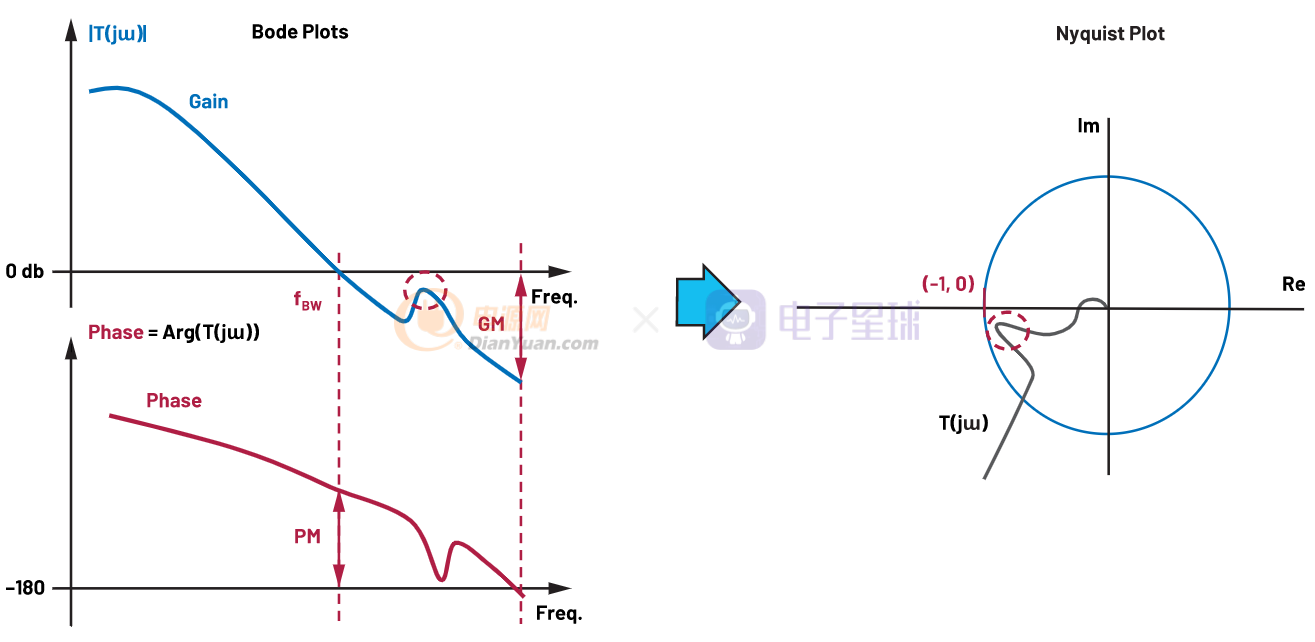
图 5. 具有良好 PM 和 GM 的概念系统,但存在不稳定的风险
总之,伯德图方法在回路稳定性分析中既简单又成功。因此,它被广泛用于线性反馈系统,包括电源。工程师只是喜欢使用相位裕度来确定和量化环路稳定性的简单性(谁不喜欢?)。许多现场工程师可能已经忘记了学校教科书中最初的奈奎斯特概念。需要指出的是,Nyquist 准则和 Nyquist 图的概念仍然有用,尤其是在出现异常和令人困惑的 Bode 图时。
电源回路稳定性
有两种主要类型的电源:线性模式电源和开关模式电源 (SMPS)。线性模式电源相对简单。它们的补偿网络通常集成在 IC 内部;因此,用户只需遵循数据手册中关于最小和最大输出电容要求的指南。SMPS 通常具有更高的效率,因此比线性电源具有更高的功率水平。许多 SMPS 控制器允许用户从外部调整补偿环路以获得最佳稳定性和瞬态性能。
由于开关动作,SMPS 是非线性的时变系统。但是,它们可以用平均小信号线性化模型建模,该模型在电源开关频率 f SW /2 内有效。因此,可以应用使用 Nyquist 和 Bode 图的线性控制回路稳定性分析。通常,SMPS 的最大带宽约为开关频率 f SW的 1/10 到 ~1/5. 通常 45° 的相位裕度是可以接受的,尤其是对于降压转换器。首选 60° 相位裕度,这不仅是一个保守值,因为它还有助于使闭环输出阻抗图变平,以实现良好的配电网络 (PDN) 设计。通常需要 8 dB 至 ~10 dB 的增益裕度,但应记住,平均模型及其波特图仅在 f SW /2 时有效。
此外,为了衰减反馈补偿环路中的开关噪声,需要在 f SW /2 处实现 ≥8 dB 的增益衰减,作为另一个增益裕度或增益衰减设计指南。


