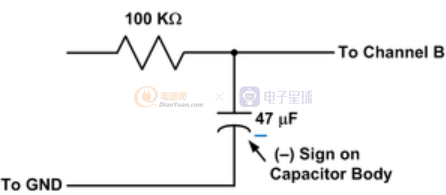
电容器由两个导体组成,通常称为“极板”,由称为“电介质”的绝缘材料隔开。在电路中,电容器的使用方式是在每个板上产生相等和相反的电荷。电荷是由导体中自由电子的积累或耗尽产生的。电荷在电介质中产生电场,从而在极板上产生电压。对于板上的固定电荷 Q,板上的电压V由电容值 C 根据以下关系确定。
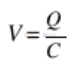
如果我们想确定电压和电流之间的关系,重新排列方程如下是有用的。
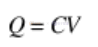
由于电流是 Q 的时间导数,因此取每一边的一阶时间导数 - 注意 C 是常数 - 会产生一个表达式,将电流与电容器中电压的变化率联系起来。
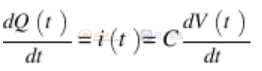
这可以明确地写成电压变化率。
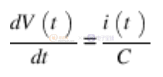
我们可以使用这个方程来研究电容器的充电。如果我们有一个恒流源 I,电容器将以每秒 I/C 伏特的恒定速率充电。在 RC 电路中,我们有一个与电阻串联的电压源,而不是电流源。当 5 V最初应用于电路时,它都出现在电阻器上,因为电容器上的初始零电压不能立即改变(当然,除非我们有无限电流可用)。在第一个电路中,电阻两端的 5V 根据欧姆定律产生 5V/100K 安培的电流,开始为电容器充电。然而,当电容器充电时,电阻两端的电压会按照基尔霍夫电压定律下降,从而降低电流和电容器电压的变化率。该过程使电容器电压的增加速度呈指数减慢。
RC 电路中的充电速率取决于 RC 乘积,通常称为“时间常数”,由希腊字母 tau 表示。在一个时间常数内,充电电容器将从其当前电压移动 63% 到通过电阻器施加的电压。施加阶跃电压V T的 RC 电路中的电容器电压V C由以下等式控制。
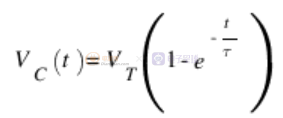
在一个时间常数中,电容器达到施加电压的大约 63%,在五个时间常数中达到大约施加电压的 99.3%。从实际角度来看,电容器充满电所需的时间通常被视为五个时间常数。在第一个电路中,时间常数为 (100 KΩ)*(47 μF) = 4.7 秒,使电容器充满电的时间约为 23.5 秒。充电和放电的时间常数相同,因此当通道 A 的电压降至零伏时,电容器完全放电大约需要 23.5 秒。
结论
1.电容器储存电荷。
2.当使用与电阻串联的电压源对电容器充电时,电容器电压的变化率呈指数下降。
3.RC 电路的特点是 RC 积,称为时间常数。
4.一个简单 RC 电路中的电容器在一个时间常数内移动到其电流值与施加在电路上的阶跃电压之差的 63%。
5.电容器完全充电的普遍接受时间等于五个时间常数。


