第六章 储能元件
这一章,主要增加了两种储能元件的介绍:电感,电容。个人认为加上了电感和电容之后电路分析的复杂难度开始上升。
储能元件用在直流电路还好,只需列出KVL、KCL公式,结微分方程即可得到结果;但用在交流电路时,这两个知识碰在一起,就像星球相撞,蹦出来好多概念和应用。比如复数,功率因数,有功功率,无功功率,频率响应,谐振,滤波等。从标量分析到相量分析,实数域到复数域,时域到频域,整个电路的分析多了一个维度,多了好多定义和分析方法。
电容
电容是由两块金属板组成,金属板间隔内充满不同的介质(云母,绝缘纸,空气),可在介质中建立电场而具有电场能量。
电容的元件特性:
q=Cu
电容的特性曲线:
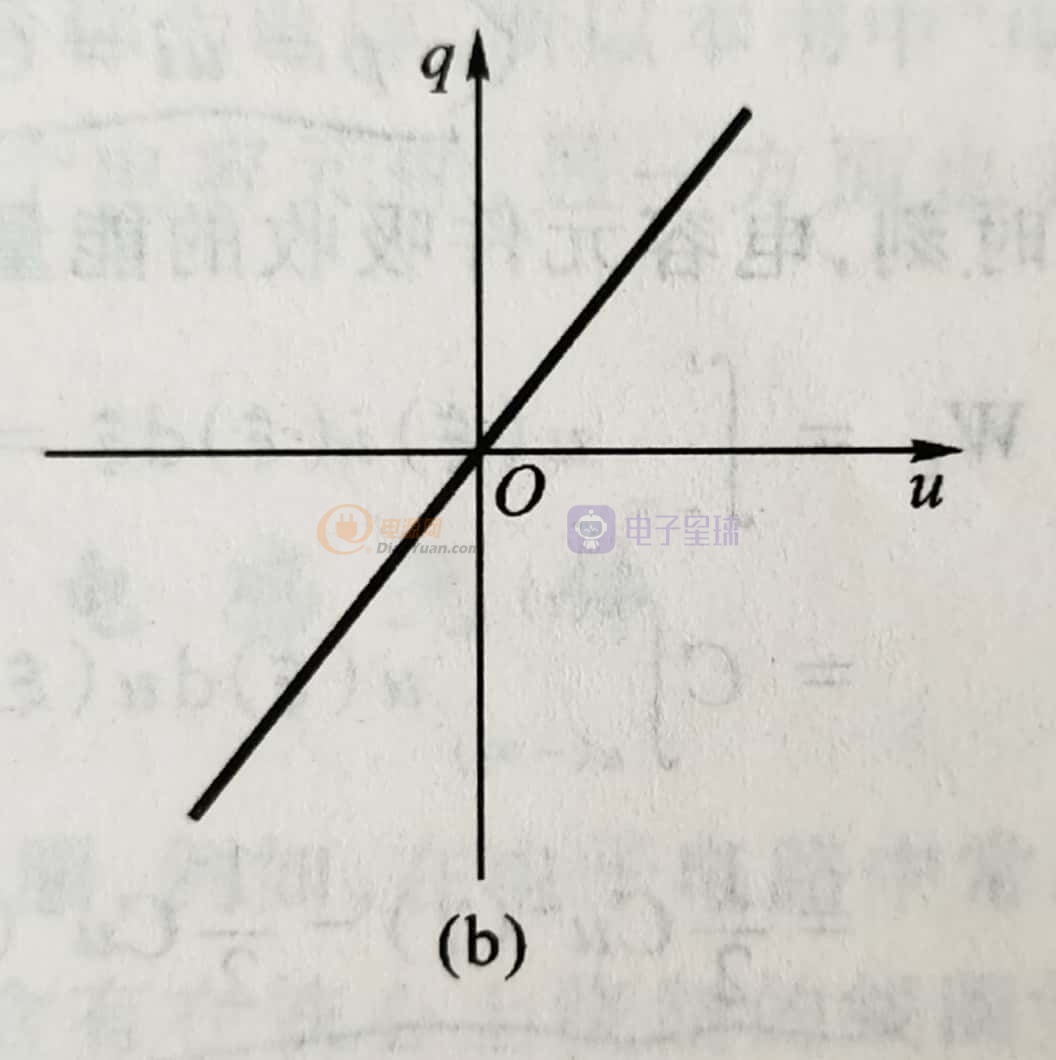
库夫特性曲线(电荷的单位库伦),电阻的特性曲线为伏安特性曲线。正如前面所说,特性曲线,是要寻找可以描述元件性质的曲线。不一定非要是伏安特性曲线。对于电容来说,电流和电压和关系不可以描述电容的性质。
电荷的流动就是电流,电容的电流和电压关系:

电容的电流与其两端电压变化率正比。如果电压一直不变那么就没有电流,相当于开路。这就是电容隔直的作用。
电容器是由两个金属板组成的。生活中也会存在这种结构,所以电容的这种储存能量的效应在别的场合也存在,这就是分部电容和杂散电容。理论上,有电势差的两个物体之间就应该存在这种电容效应,可能电势差太小,面积太小,或者距离太远等导致电容效应太小,可以忽略。但是在要求严格,计算精密的场合是不可以忽略的。
电感
电感元件是由导线绕制的线圈,是一种反应了电流产生磁通和磁场能量储存的一个理想模型。线性电感元件的元件特性:

电感的特性曲线:

注意:这是电流和磁通链的关系,磁通链的单位Wb(韦伯),所以这个就是韦安特性曲线。
根据电磁感应定律,可得电感的电压电流关系:
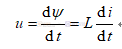
通过上式可以看出:如果电流是个直流电,则没有电压产生,这个时候电感就像一个普通的导线。如果电流高频变化,则会产生电压、电感阻交。磁感线都是一条条封闭的曲线,在多条靠近的电感同时工作时,不仅会有自身的磁场,还会受到其他磁场的影响,也就是说除了自感还会有互感(后面会详谈)。
储能元件的串并联
串并联的基本准则就是伏安特性相同,过程不赘述,结论如下:

如果有写错的地方或者有什么新想法,欢迎大家评论指导。


