本小结介绍滤波环节即单相逆变电路的LC滤波。
根据上一节可知,单相逆变器的桥式电路输出的方波信号内包含工频信号以及与开关频率相关的高频信号,因此为了令逆变电路输出标准的正弦波,需要“去除”高频信号,这个环节就是滤波环节,更详细的可以理解为低通滤波环节。就是频率低的调制波信号可以通过,高频的杂波不能通过。
经典的低通滤波器就通过LC串联形成。
LC滤波电路可简化为:
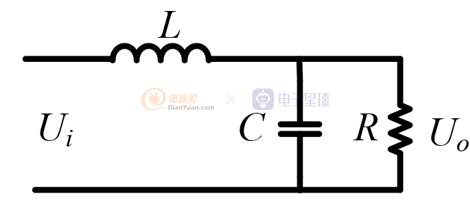
LC滤波电路
其中:L滤波系统的电感,C为滤波系统的电容,R为逆变器的负载。
在交流通路分析可知,电路中电感和电容的阻抗分别为:

则根据基尔霍夫定律可知
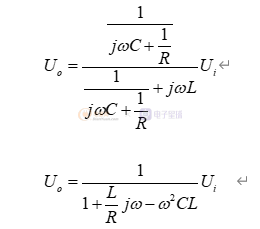
则LC滤波的电压传递函数可表示为:
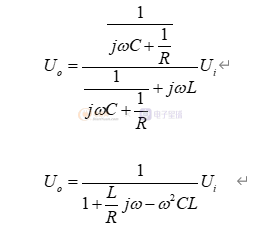
其中:为自然震荡角频率,的值代表着该二阶系统的转折角频率;为阻尼比。可见LC是一个二阶震荡系统。其频率特性可化简为:

LC滤波系统的转折频率为:
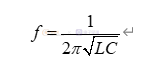
LC滤波系统的Bode图如所示
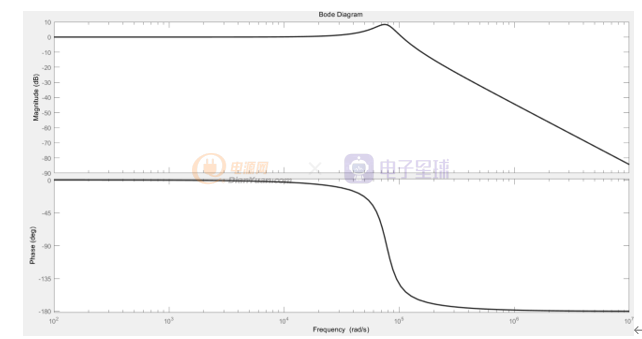
LC滤波系统Bode图
LC滤波系统的滤波效果取决于滤波系统中电感和电容的值,根据LC滤波系统的Bode图可知,LC系统对大于转折频率的谐波有明显的抑制作用,对于小于转折频率谐波无抑制作用。因此转折频率是滤波性能的关键参数。若转折频率太小则滤波系统对工频信号有抑制作用。若转折频率太大则对在开关频率上的谐波抑制作用不明显,输出电压谐波含量较高。根据经验,可取转折频率为开关频率的十分之一,这样即可以保留工频信号,又能有效抑制高频谐波。
接下来通过两个方式设计滤波环节:
1 LC串联
本文仿真开关频率:5000Hz,期望输出频率50Hz,输出电阻100Ω。本文选择滤波电路的截止频率为500Hz。
假设令L=1mF计算可得:C=10.132mH。低通滤波器在线计算网站:
https://www.bchrt.com/tools/resonant-frequency-calculator/
仿真图如下:

输出电压如下
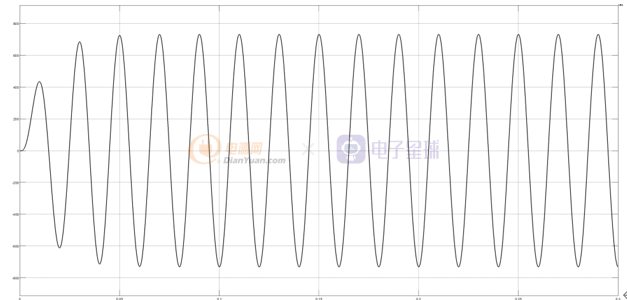
FFT分析如下:

500HZ以后的滤波几乎全部被滤除,效果理想。
2 滤波模块
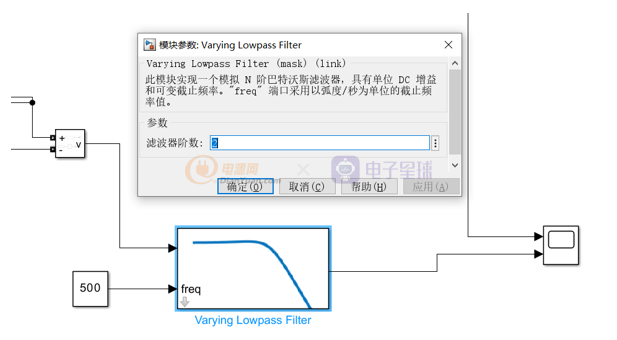
巴特沃斯滤波器,设置阶数,输入为信号以及截至频率。本文设置截至频率为500Hz,阶数为
2。
输出电压为
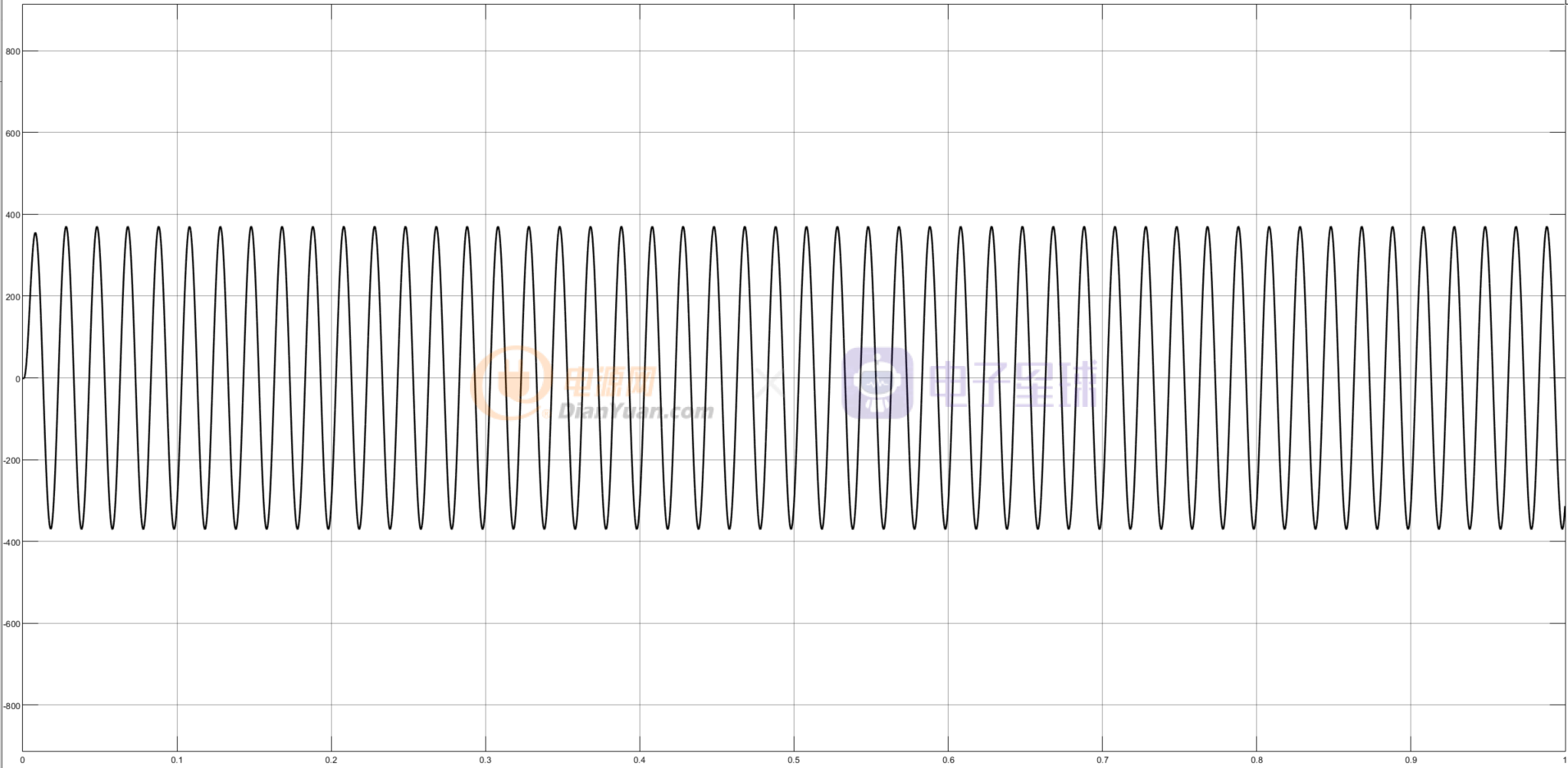
FFT分析为
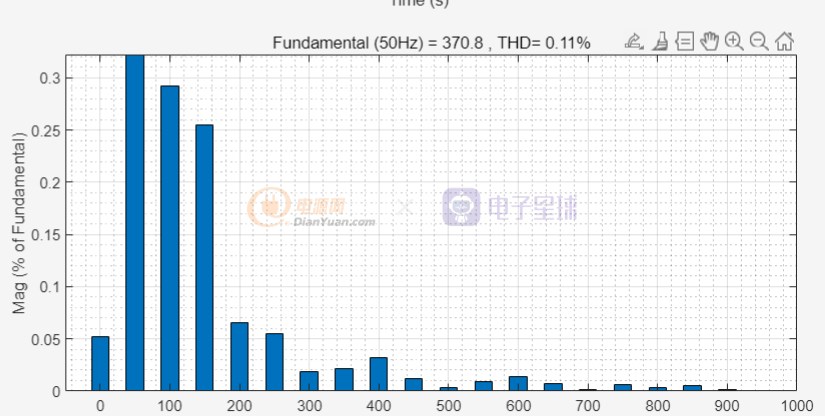
500-1000Hz的内存在少量和谐波,是因为采用2阶巴特沃斯滤波器导致的,若用更高阶的巴特沃斯滤波器则会有更好的滤波效果。
输出电压对比
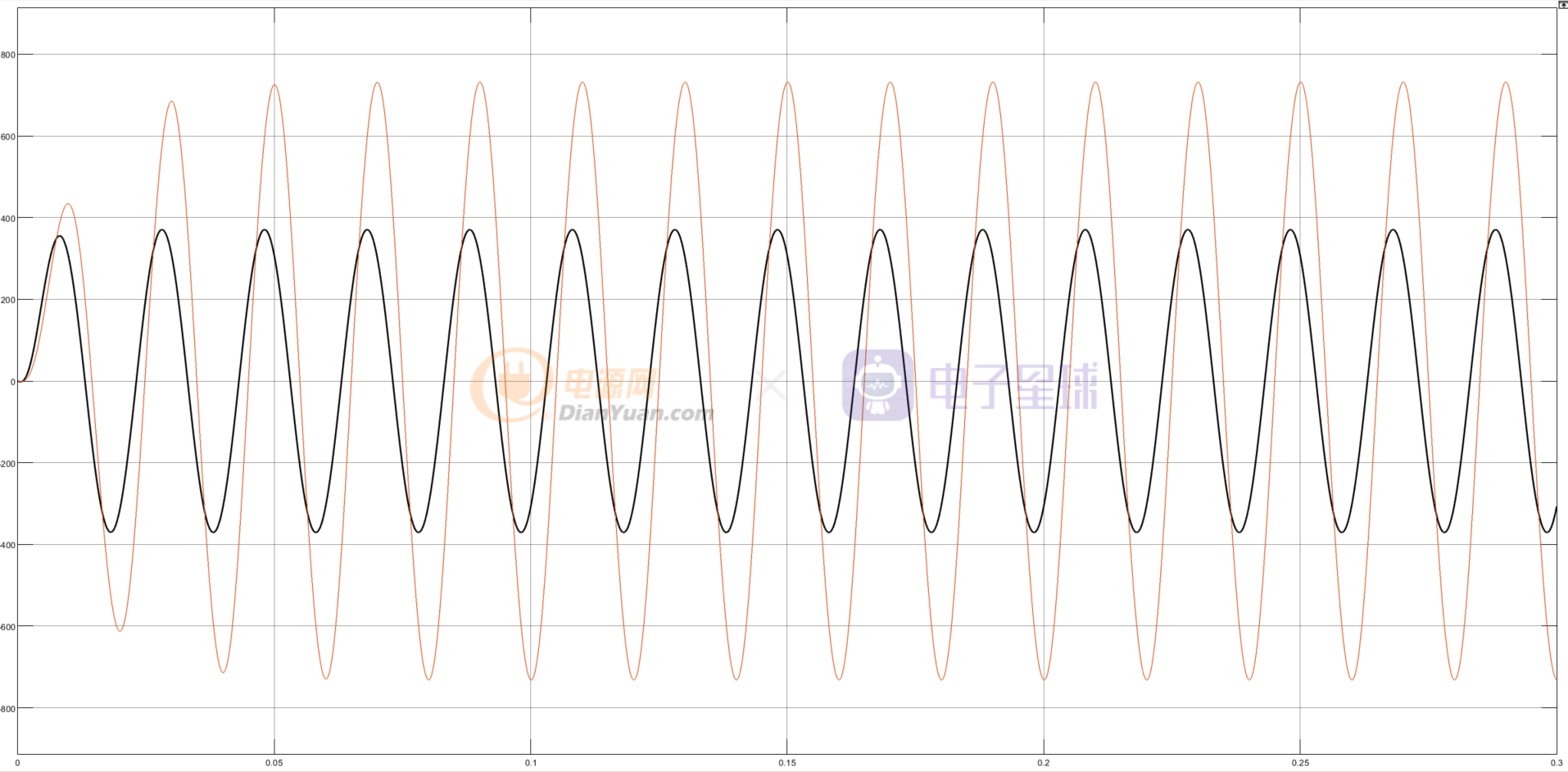
一直输出电压均为标准正弦波,因此可以分析两种方式均可以对高频谐波进行去除,但通过LC滤波的方式进行滤波的输出电压会大于方波的电压(什么原因还未分析出)。初此之外,两者的输出电压相位有略微差别,因此造成改现象的原因为两个环节的传递函数不同,相位响应不同,因此输出电压相位不同,下一章节将通过传递函数的形式对LC滤波电路进行验证。(一切低通低通滤波器都可以以传递函数、幅值响应的角度来解释,截下来对两个滤波器的产地函数进行详细的分析)


