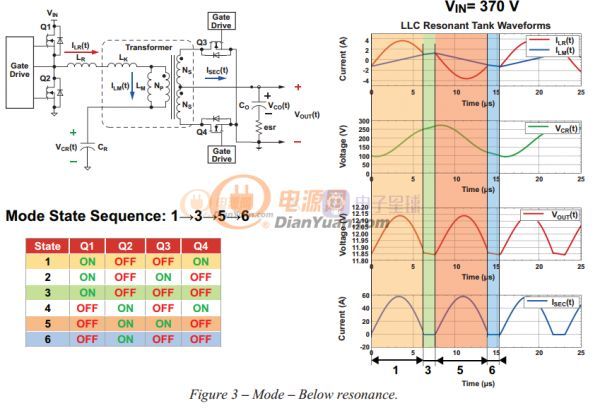
拓扑:半桥 + 不控整流
对于BUCK来说,轻载指的是输出电流减小,Udc升高,通过反馈减小占空比使整流侧处于DCM模式,即靠PWM的占空比调整实现的,可用二阶充放电回路原理分析具体的电流形式。
对于LLC来说,占空比恒定,属于变频调制,谐振下的轻载 、 次谐振下的重载 都会出现DCM模式,但这两种DCM模式有着本质的不同
前提:基波分析法
% 基波分析法指的是电流的基波,没有基波电流,则不存在基波分析法,基波的周期决定于具体的L-C值。
% 对于单独的L-L-C串联谐振电路来说,器件上的电流、电压都是基波形式。但是,对于LLC变换器来说。即使在谐振下,也并非每个器件上都有基波形式的电压,如,Lm被钳位时,并联形式的Lm和励磁线圈,对外表现为”基波电流、恒定电压“。基波电流直接决定于输入阻抗的频率特性,这就是LLC基波分析法的要点。
众多资料(如TI的LLC converter small signal modeling)的波形分析中可得两点:
1---任何开关周期下,谐振的充要条件<===>Lm被钳位,Lr Cr参与谐振,谐振的基波电流与参与谐振的Lr Cr大小有关,基波分析法成立
2---Lm不被钳位,即参与谐振,重点在这里,此时,并不是众多资料上说的那样,Lm 参与谐振与 Lr的电流相等,如果真是这的的话,那下面彩色图中”3“阶段的电流应该是正弦的。。。而是C -Lr-Lm-Cr(上开下关)构成的充放电回路。只是这个过程比较短暂,可进行线性化,C指Q1的结电容
----补充一下:忽略等效R时,对于L-C形式的充放电回路,只能用基波分析法,基波周期决定于L-C元件 ,如是考虑电路中的R,则表现为二阶电路。
因此,Lm不被钳位时,例如下图阶段3中,可知,L-L-C的总体电压在上升,而MOFET的结电容C的电压却在减小,即,所谓的L-L-C均谐振,实际指的是Q1的结电容给C---Lr----Lm---Cr--构成充放电回路 。如果要分析此时段的谐波电流,可忽略Q1的结电容,分析Vin--Lr---Lm---Cr回路即可。基波频率决定于Lr---Lm---Cr的值。应该有文献分析过,图中并没说明。
总结:
LLC只有一种工作模式,即充放电模式,充放电的谐振频率,即基波电流的频率决定于参与充放电的L-C的大小,
只不过开关周期T、充放电的电流基波周期t,死区时间,使得模式变得复杂。或者说,
通过控制开关周期、死区时间 (即控制在一个开关周期T内,二次侧充放电的基波电流能否完成一个周期的换流)把Lm切入L-C充放电回路的本质是当电流进入换流模式时,电压方程是不同时满足。
通过轻载把Lm切入L-C充放电回路的本质是,可强迫原充放电回路中的基波电流发生阻断,
以上两种控制形式就像开关一样,可切换Lm是否参与L-C的充放电回路。
=================================
基于以上两点可得
1)
fs
注:t3时段 Lm上的电压其实比前面时间要小,因为Q1的C- Lr Lm Cr 的充放电回路中,基波周期比Lr Cr大,电流上升速度必定减缓
这一点并非是大多数资料中,DCM时,Lm上的电流仍按原速率线性上升,显然DCM时,充放电回路也可用基波分析法,只是时间太小了近似于线性充放电。否则电路分析太杂。而是一般的KVL KCL
总结:
a: fs
结论:这种DCM模式是由原边引起的,称主动DCM模式
(图片:TI LLC converter small signal modeling)
2)
fs=fr时的DCM:
fs=fr时,也会出现DCM模式,如下图b(华科论文)
应该怎么分析这种轻载模式?
直观上,可从基波电流角度分析,输出端的基波电流减小,以至于基波励磁电流减小或消失,此时进行DCM模式
,
总结:轻载-----整流侧基波电流回路被切断-----强迫阻断原边基波电流,使LM加入原谐振回路,构成新的充放电模式------------新的基波周期=f(fr fm cr)
结论:
t3-t4:是由负载引起的DCM模式,称为被动式DCM模式
t4-t5:是由原边开关模式切换成了充放电模式,其DCM原理与fs
====================================
要说明的是,对于LLC变换器的DCM模式 CCM模式,主要指基波电流的连续和断续,Lm被钳位是,基波=f(LR CR),Lm不被钳位时,基波=f(Lr Cr Lm) 是不是两种基波电流情况下 Lm都能被钳位?如果只考虑二次 侧的整流电路,当然可以对任何正弦电流进行全波整流,但对于LLC,当然不是这样,因为Lm参与L-C充放电回路后,Cr电压变大,导致二次侧VD反偏,最终原边电压<原来的n*Udc,可勇者TI的LLC小信号建模