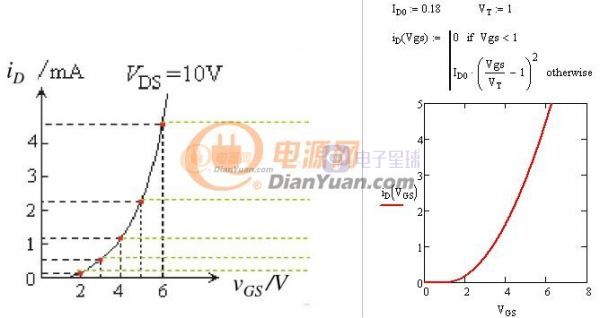
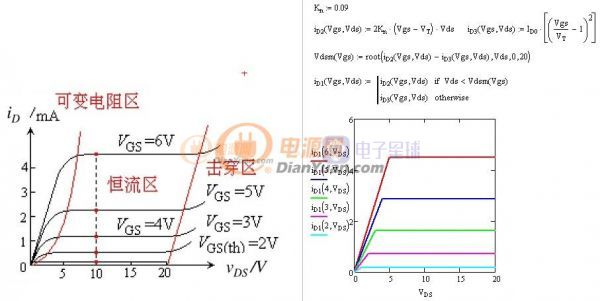
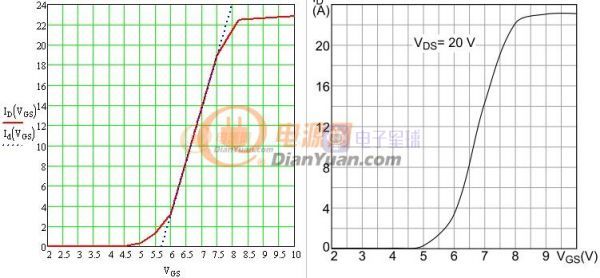
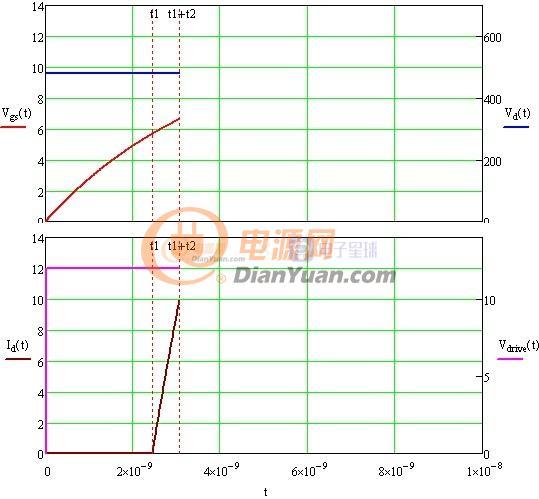
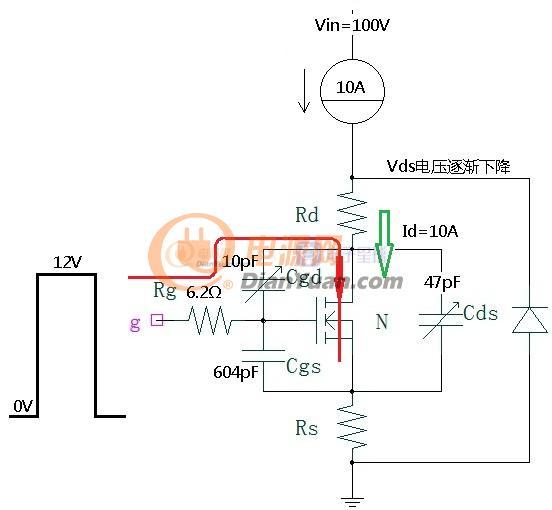
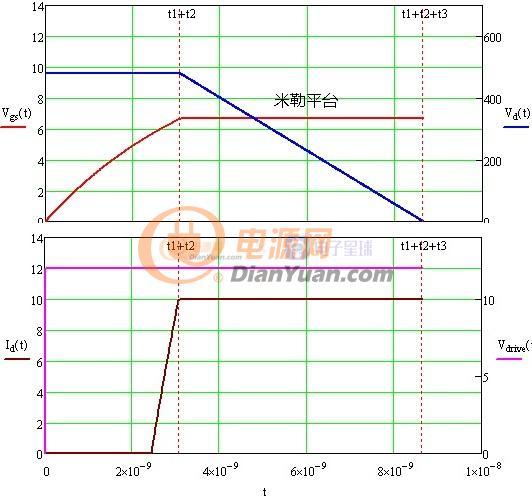
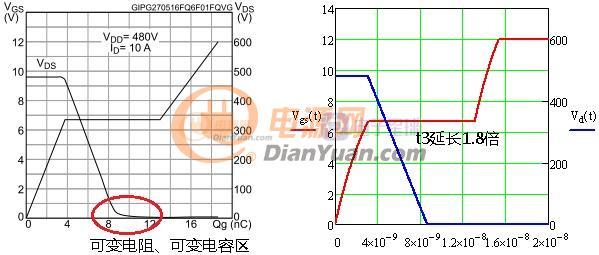
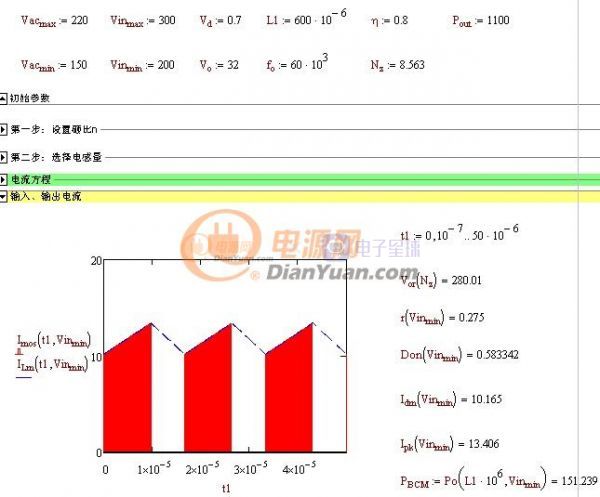
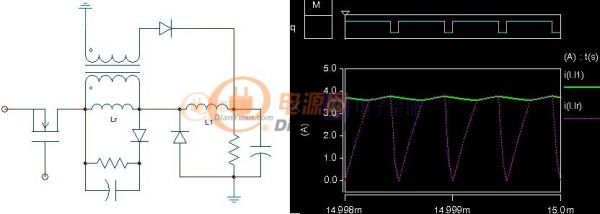
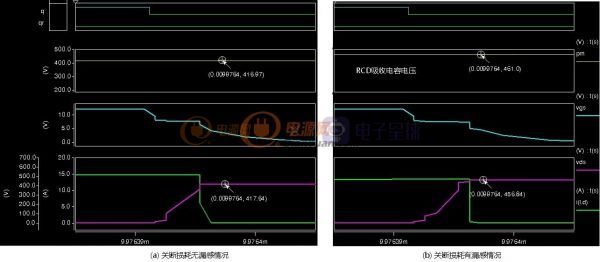
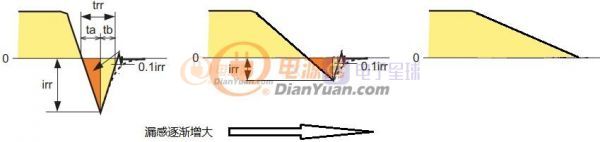
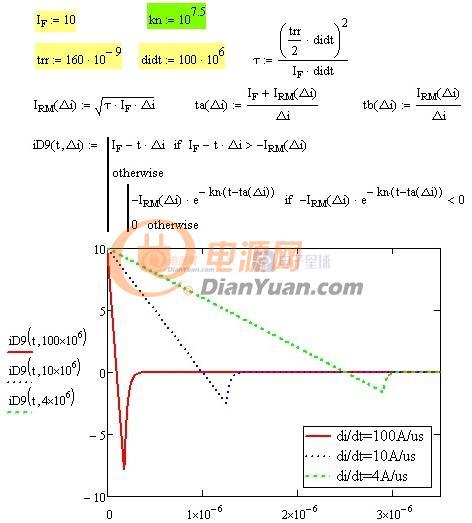
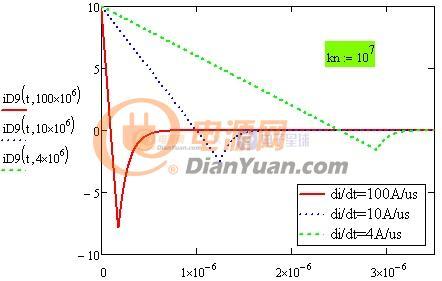
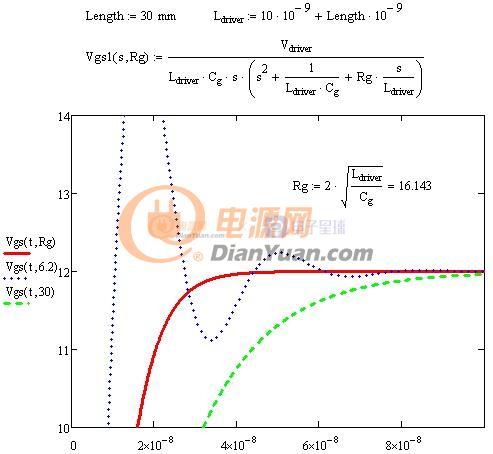
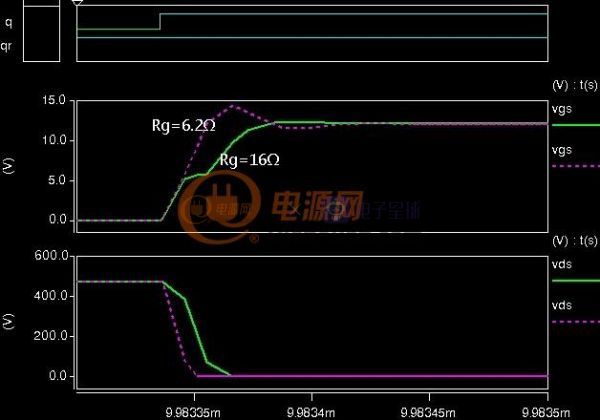
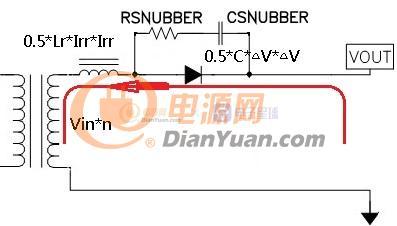
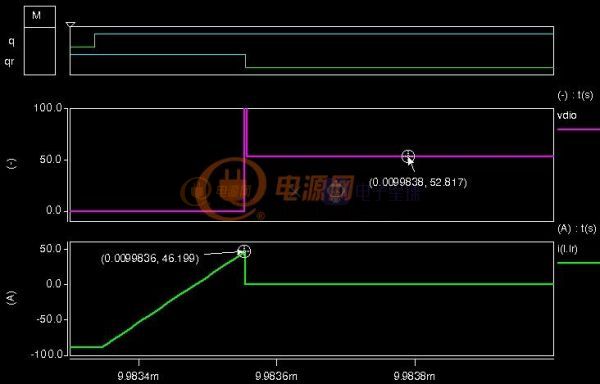
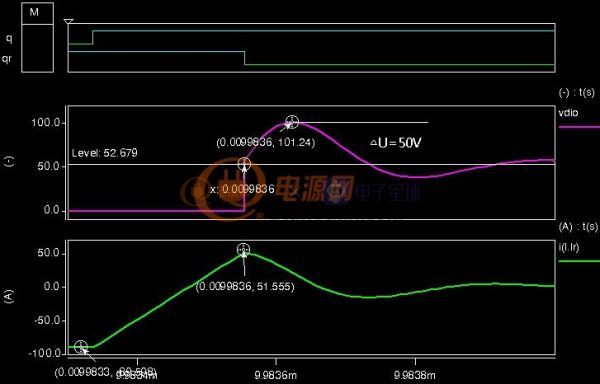
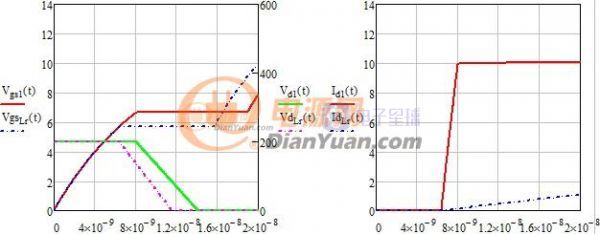
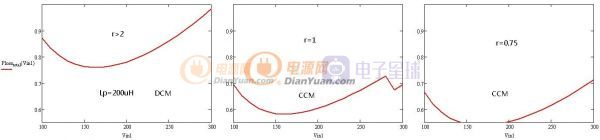
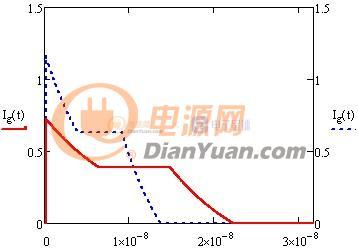
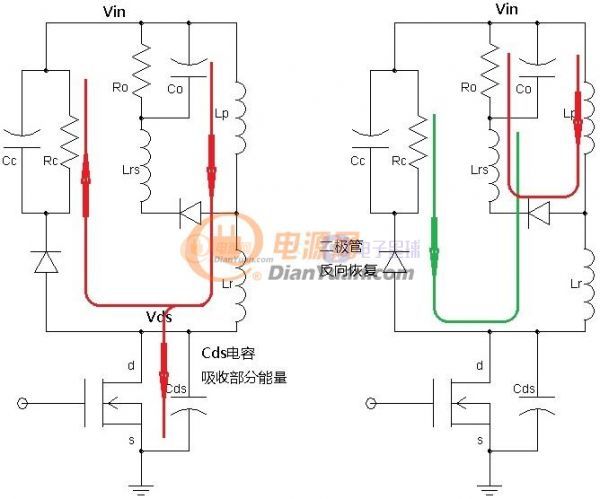
当开关电源完成初步设计后就可以进行下一步的优化设计了,所谓优化设计就是为当前的方案选取最合适的器件以及为选取的器件配置最优的参数。开关电源中对效率影响较大的是开关管(包括二极管)和磁性元件(包括导线),在以往的设计参考资料中会给出一些一般取值,当建立了损耗模型后估计可以用公式把这些最优参数推导出来而不再依赖经验值了。此贴就准备结合Saber和Mathcad软件对MOS管的损耗分析进行学习和探讨。
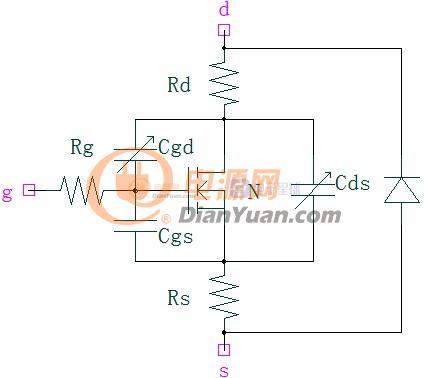
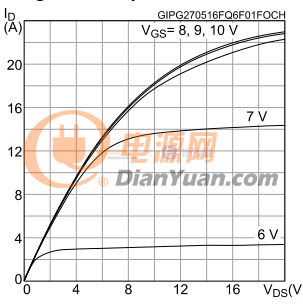
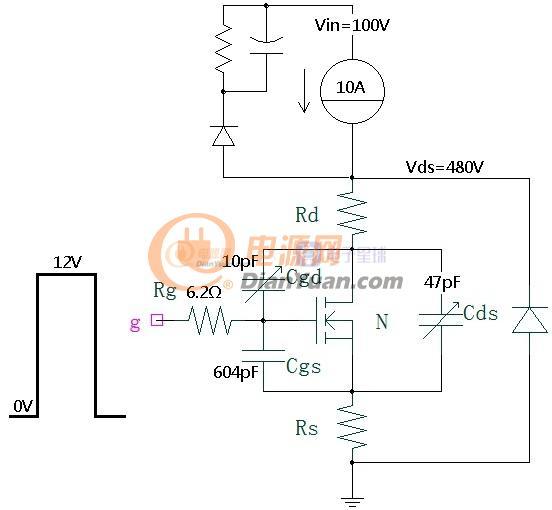
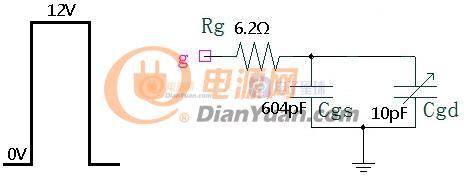
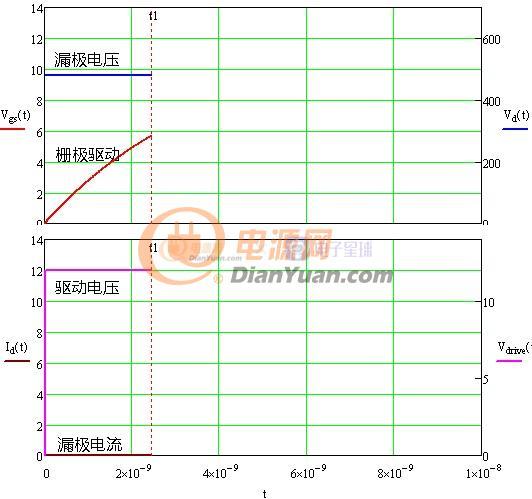
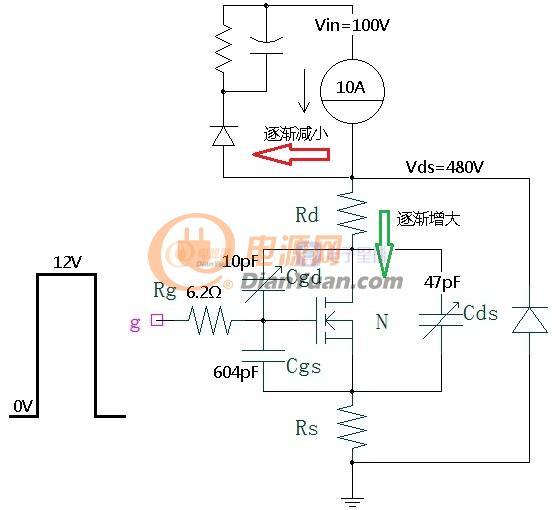
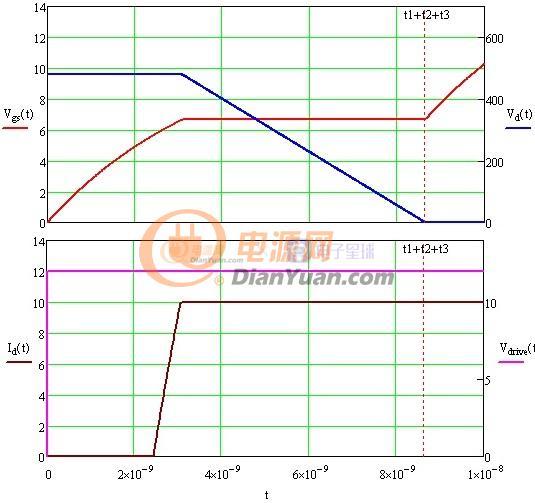
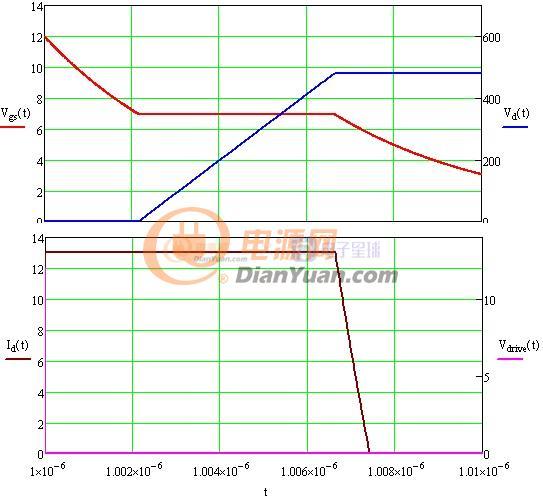
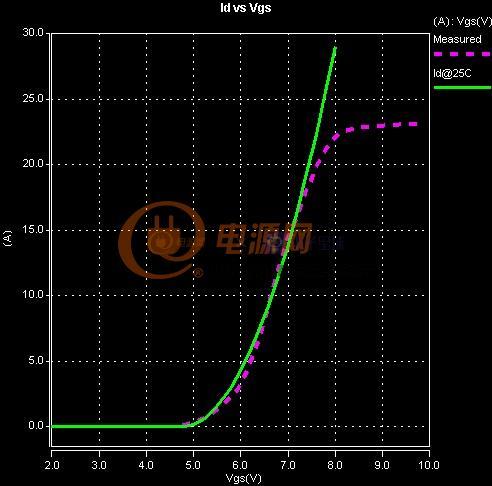
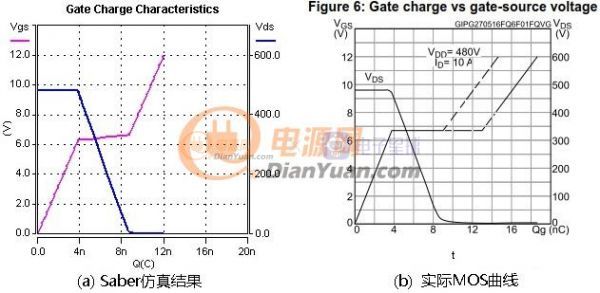
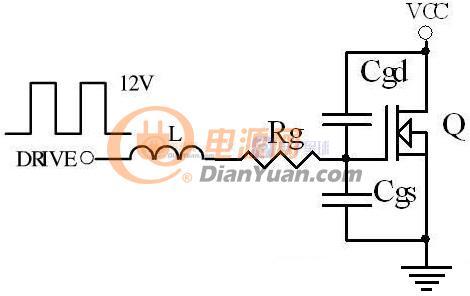
图1-1 MOS管模型
MOS管型号:/upload/community/2019/01/12/1547260663-25030.pdf
参考资料:https://wenku.baidu.com/view/92e0920c998fcc22bdd10dad.html?rec_flag=default&sxts=1547255081442