声明:
本文是业余时间的思考成果展示,其中可能有不太正确的地方,欢迎指出!另外不注明原作者的转载都木有小JJ!
背景简介:
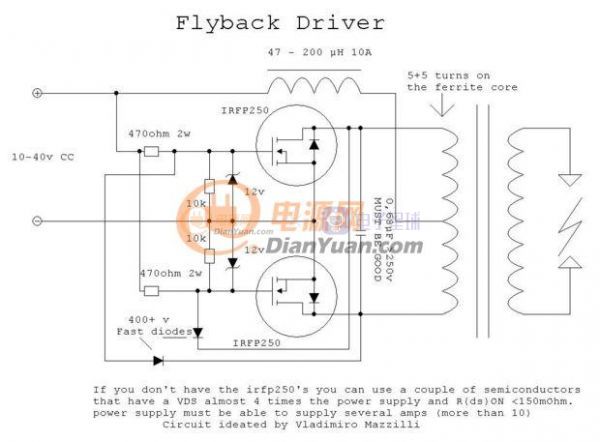
ZVS双管自激电路(以下所有ZVS均指这个电路而不是零电压开关除非特别说明),基本上每一个在论坛上玩高压或者电路的同学都做过或者至少听说过的一个电路。如下图:
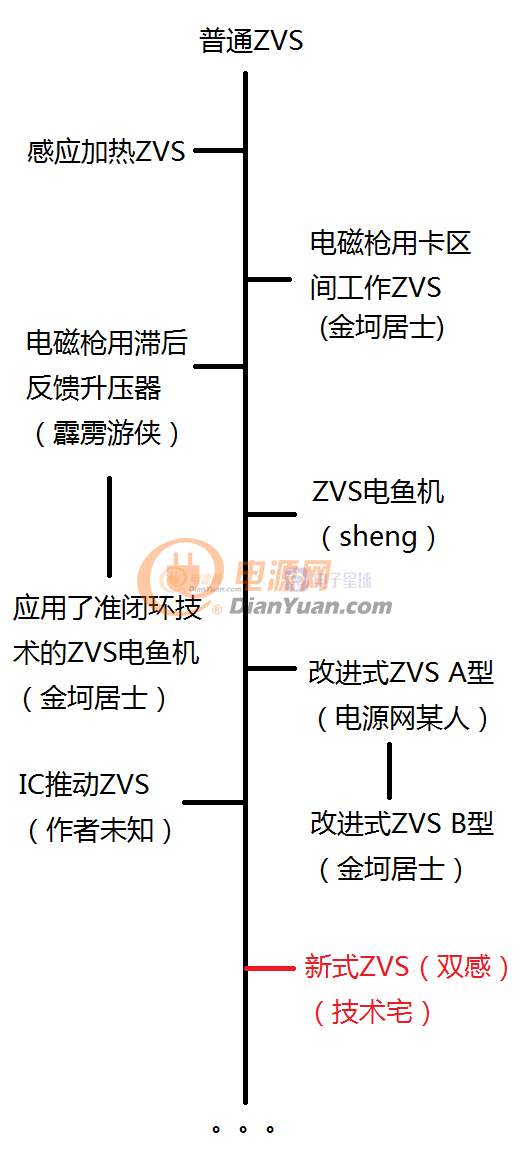
还有隔壁科创论坛的yanli12321同学发明的双电感的无抽头变压器版本,这里就不贴图了,空降地址就是前面的链接。在中二时期,窝还尝试过给ZVS加上稳压电路,有滞回比较器法还有间歇使能的准闭环(带空载输出过压保护的ZVS电鱼机和第一次准闭环ZVS的想法),在缺少理论论证的情况下进行的设计,效果并不是很细想,很多现象无法解释,某些蜜汁故障无法确定原因无法排除。还有一个当年的黑粒屎教程...尽管如此,ZVS还是给论坛各位包括窝的学生时代留下了十分美好的回忆,下面是中二时代的ZVS发展历史:
虽然被制作过了无数遍,但是这个电路的工作原理确从来没有一个详细的解释,唯一的分析就是科创论坛上面的这篇文章,但是他也没有一个详细定量的分析。这就是这片文章存在的意义!有史以来第一次定量分析ZVS的工作原理并为元器件的选择和工作点的设置提供指南。而且窝经过分析和仿真得出一个震惊的结论,ZVS里面两个MOS会有一定共通时间,而且这个共通时间对于正常工作来说是很关键的。好奇为啥?那就继续往下看吧。
在阅读了以色列Ben-Gurion University of the Negev大学Daniel Edry的一片IEEE学报(Capacitive-Loaded Push-Pull Parallel-Resonant Converter, 会议和期刊版)之后,结合仿真,窝提出了一组适用于分析zvs的方法。注意,这个帖子给出的方法只适合于全波/全桥整流滤波型负载的ZVS,而阻性或者弱感性负载(比如感应加热,非整流滤波的高压电弧)不在本贴讨论范围之内,带整流容性负载和阻性负载的时候,ZVS的特性是不一样的,这个值得注意。窝会在另一篇帖子里给补全的,本帖只分析整流滤波负载的ZVS。
继续Edry前辈的故事:
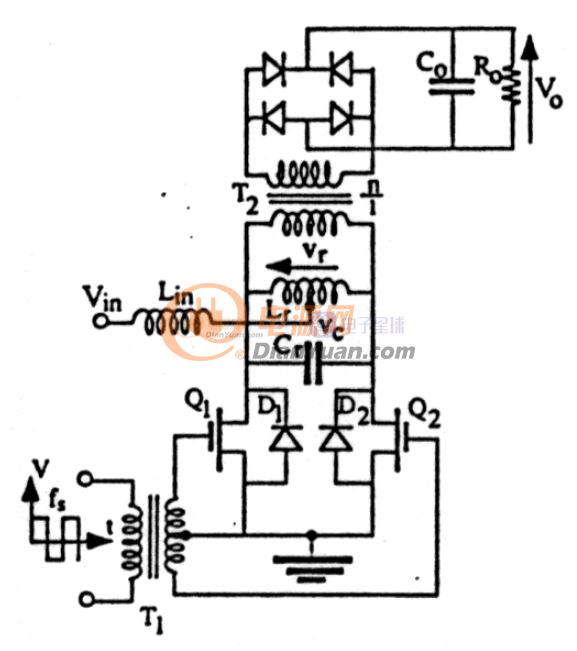
在Edry的文章里介绍了一种它激变频固定占空比的电流源供电的并联谐振变换器(Current-Fed Parallel Resonant Converter),如下图:
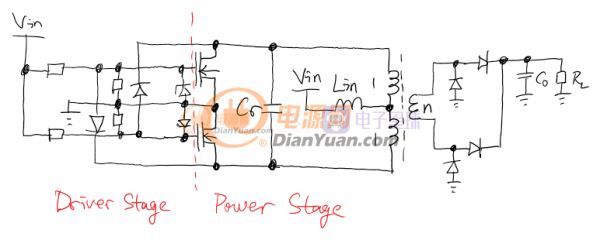
光看功率级部分完全是和ZVS一一对应的! 窝的分析方法绝大部分地方借鉴了Edry的思路,窝稍微改进了下,使得分析时所有的量都是实实在在的可以测到的物理量,Edry的模型里有些量并没有实际对应的物理量,虽然没错但是好不方便实践测量...被分析的ZVS电路如下:
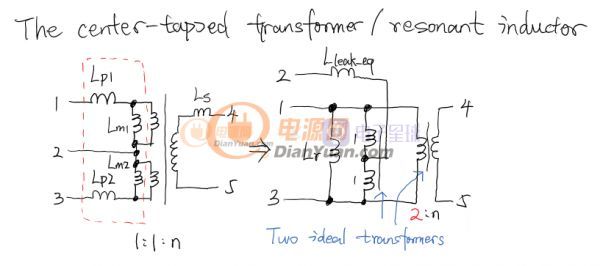
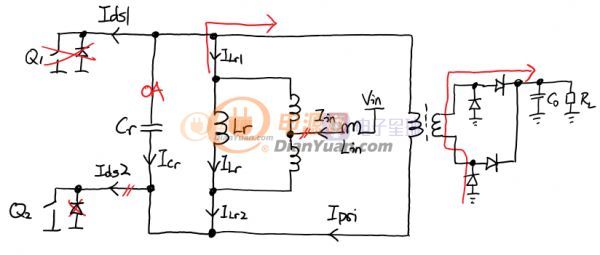
在分析的时候先只看功率级也就是Power Stage。为了分析功率级特性,先把自激部分去掉,改用外部固定频率进行驱动。首先是处理变压器(匝数比1:1:n)抽头的问题,变压器初级是一个有抽头的电感器,在同一磁芯上同向绕制的两个的线圈的总电感量是两个电感量与2倍他们之间互感之和。Lp1和Lp2两个初级的漏感会影响下图里1-2和2-3脚的电感之间的耦合,具体多少不用管,这样两个初级的耦合效应会在测量1-3脚电感时被算进来,实际中只需简单测量1和3脚之间的电感量即可确定谐振电感Lr。因此这里可以把初级部分看作Lr和一个1:1的理想变压器,其余部分则看作是2:n匝数比的理想变压器。Ls是次级漏感,实际中对电路工作有一定影响,后面会进行分析的。变压器和谐振电感的分解见下图:
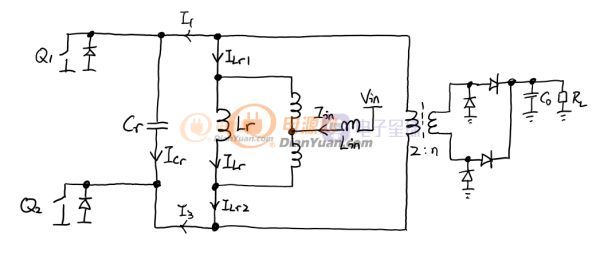
拆分之后的等效电路如下图。注意I1和I3分别对应实际变压器1脚和3脚的电流,Iin是ZVS的输入电流,也是变压器抽头的电流。ILr, ILr1和ILr2都是实际中测不到但是有物理意义的电流。
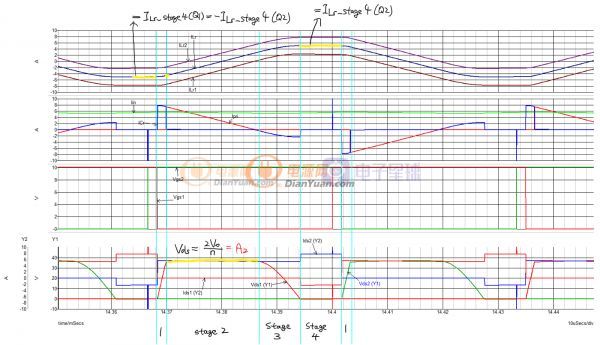
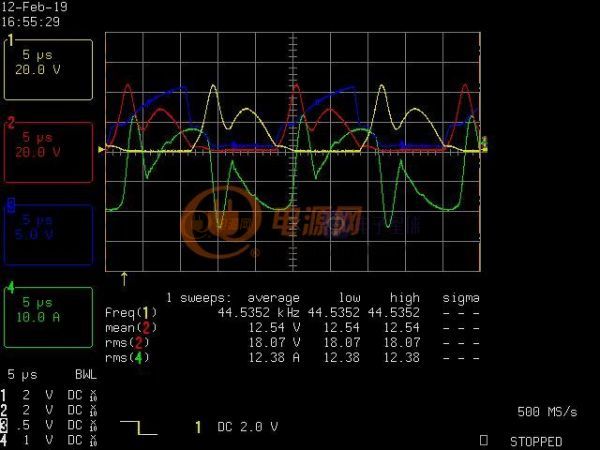
现在可以开始正式的稳态分析了。这个电路一共有8种状态,其中的两两对应(Q1 Q2开启时分别有4种),于是可以简化成四种状态,下图展示了ZVS带整流负载的稳态波形(看不清的话附件有高清大图):
在进入状态1之前,我们假设Q1和Q2同时都在导通。什么?!做过电源的朋友都知道一般半桥和推挽最怕两个mos管同时导通,但是这里为什么可以呢?思考一下,这里的输入有一个大电感,在开关频率的范围之内,每个周期之内的输入电流几乎是不变的,于是Vin和输入电感可以等效为一个电流源。电流源最怕的就是开路,因为电流没地方去了,它会升高电压使劲找地方让电流维持流动,两个管同时关闭会让任何电流通路消失,Vds急剧升高于是就爆炸了。所以在这种电流源输入的电源里两个mos管一定要有共通时间,千万不能两个管同时关闭。因此窝怀疑Edry文章里的驱动电路可能有些不妥,他用了一个变压器产生两个反向的方波,可能没有足够的直通时间。
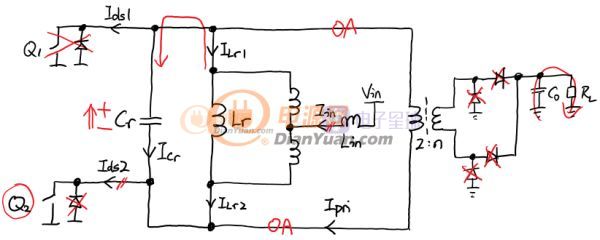
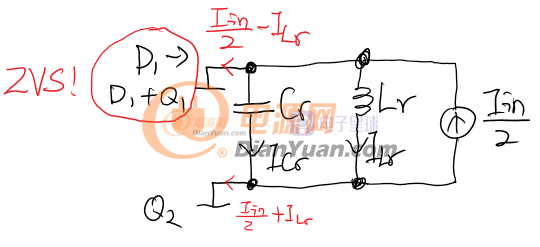
状态1:以Q1的关断作为开始,此时Q2已经被打开,电容和电感进行谐振,此时Q2的电流约等于输入电流,电感和电容的电流是相等的。在状态1开始之前一瞬间,Q1/D1上的电流为Iin/2-ILr,而Q2上电流为Iin/2+ILr。在状态1中,LrCr谐振会导致Cr上的电压VCr不断上升,当VCr到达输出电压的变压器初级反射电压(Vo*4/n/n)时,状态1结束进入状态2。
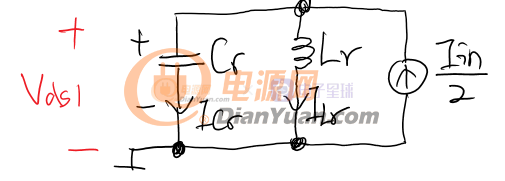
如果把Lr和自耦变压器看作一个三端网络,则可知ILr1+Iin=ILr2。1:1自耦变压器将输入电流“一分为二”,如果不看抽头,可以发现一个端以Iin/2吸电流另一个以同样的大小出电流,于是可以等效为Iin/2的电流源。状态1的简化等效电路如下。电流源的大小为输入电流的一半:
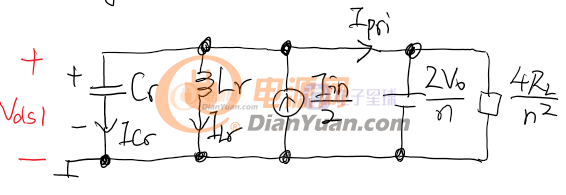
状态2:状态2开始之后,变压器初级开始接管电流,Cr开始完全不通过电流,VCr被钳位到反射电压的水平。在这期间,输入电流和电感电流ILr一起对负载供电,二次侧整流二极管开通,从初级接收能量。有等式Ipri=ILr1=Iin/2-ILr成立。Ipri是初级电流,入下图红色箭头所示。起初电感和输入电流一起为负载供电,电感电流ILr开始下降,当ILr过零之后输入电流为负载供电同时为Lr充能,ILr和初级电流Ipri继续下降(实际ILr是在往另一个方向增长!),直到Ipri过零,二次侧整流管关闭,进入状态3。
上图是状态2的电路图,其简化电路为:
状态3:状态3开始后,Cr再次接管ILr1(=ILr-Iin/2),此时Cr与Lr谐振,VCr开始呈正弦波规律下降,ILr1逐渐变成正的并且趋于平缓。这个状态中Q2的电流等于输入电流。当VCr等于0的时候,状态3结束。
状态3的简化图和状态1是一样的,只不过初始状态不一样:
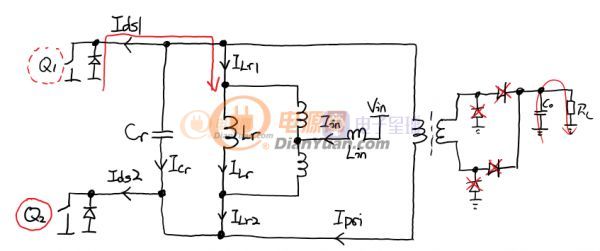
状态4:当VCr到0V之后电感电流依然是正的(图中从上往下),电流为了找到出路会打开新的通路。此时D1会导通。之后D1上的电流为Iin/2-ILr,而Q2上电流为Iin/2+ILr。在状态4中,VCr一直被钳位到接近0V,这给ZVS创造了条件(在Q2开启的时候,Vds1=VCr),Q1可以在任何时间开启,开启之后电流大部分流过Q1的mos沟道少部分流过体二极管D1,状态4维持,直到Q2关断,然后进入状态1的Q1镜像版。周而复始。在Q1开始前,Lr和Lin中的电流基本保持不变。
根据这四种状态的边界条件,可以确定状态1-3的时间以及功率级的变换比(M=Vo/Vin,在理想无损耗的情况下):
t1, t2, t3 分别对应状态1,2,3占用的时间,状态4所需的时间根据开关频率不同可以改变。M是输出电压与输入电压的比值,Wr是脚谐振频率,Zr是特征阻抗,A1,A2,A1/A2是定义的数。
之前的分析一直没有考虑变压器次级的漏感,这个漏感会在状态2的时候在VCr上产生一个尖峰,原因是因为Cr和次级漏感谐振了,这个谐振的初始条件和状态2的初始条件一样。最终可以得到漏感引起的多余电压峰值的公式,Lleak_sec是在次级测得的漏感大小,为初级全部短路时候读得的电感值:
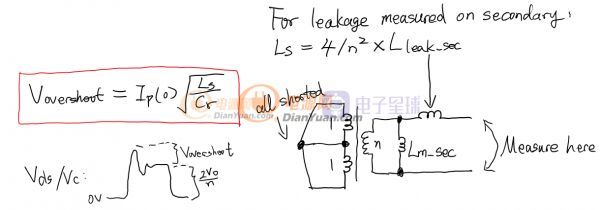
好了,到此ZVS的功率级就介绍完了。窝用的是和Edry类似的方法进行分析的,得到的结果也是基本一致的,不一致的地方主要是系数和量纲的不一致,不影响正确性。
ZVS分析!正文开始!
其实前面的这部分只能算是背景知识哦,不过有了这些知识,理解ZVS就容易多了。现在让我们来看一下ZVS的自激电路部分,当一侧的mos管的Vds开始谐振下降的时候,二极管和上拉电阻会在电压谐振到比较低的时候逐渐开启这另一侧的mos管,而逐渐开启的mos又会通过另一个二极管渐渐关闭这一侧的mos。相对慢的Vds下降,比较大的MOS管门极电阻还有米勒平台效应给了两个管子一定的共通时间,完成了正常的换向。整体看来,可以认为t4也就是Q1Q2全部开通的时间极短, 也就是说状态1,2,3占用的时间之和即等于一半频率(因为一个完整周期每种状态会发生两次哦),于是能写出下面的第一个等式,联立二式之后即可求解fs:
很遗憾,在进行了各种尝试之后,并没有能够获得一个人能看的分析姐...fs的表达式在用了某些假设近似的情况下都复杂的要死...于是...窝想到了...图表!没错!在计算机普及之前很多很难算的函数都是通过图表来查询的!于是上面的式子经过某些化简处理之后,窝通过Matlab对其求数值解并制得两张图(matlab可以打开的图和出图的m文件窝放附件里(/upload/community/2019/02/05/1549347133-91782.zip)
使用方法如下:
1. 先计算三个量,分别是自然谐振角频率,特征阻抗和归一化的负载电阻。Lr是谐振电感,就是变压器初级没抽头两端测得的电感,Cr是谐振电容,n是匝数比,变压器配置:1:1:n。
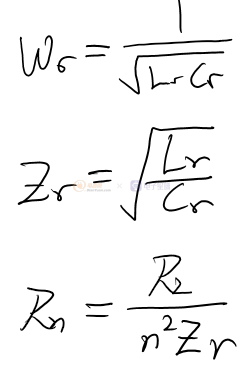
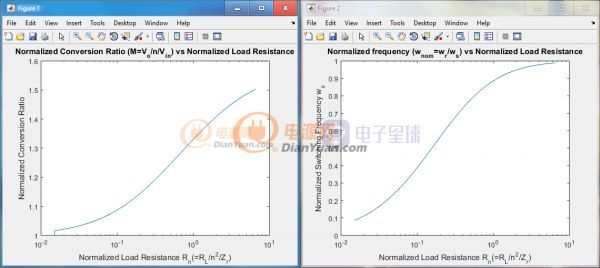
2. 通过Rn从两幅图中分别找到归一化的开关角频率(Wnom,左)和归一化的转换比(Mnom=M*n,右)
3. 通过如下公式计算开关频率fs和输出电压Vo:
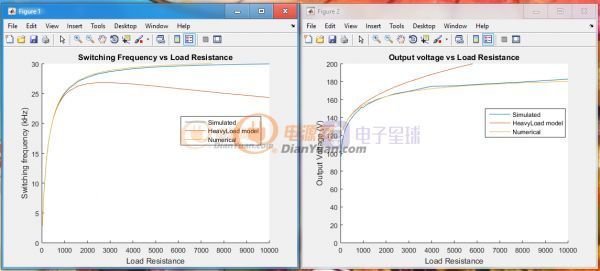
至此一个带整流滤波输出的ZVS在特定负载下的开关频率和输出电压就可以被轻松找到了。上面的方法假设了理想的器件也就是没有损耗,结果和现实中是会差一点点的。现在电脑很普及了,其实可以参考窝发的m文件里,给定Ro直接进行数值计算。Multisim和Simplis的仿真文件也在上面的附件里。以上的方法经过仿真验证,精度极高:
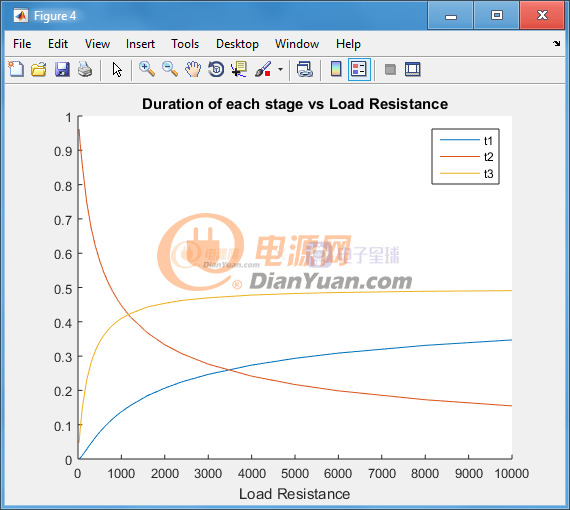
左侧是开关频率和负载的关系,右侧是升压比与负载的关系。图表的结果是黄色线,电路仿真结果是蓝色线,而这里面的HeavyLoad Model是窝算出来的一种只是适合重载情况下的分析姐,因为表达式太复杂所以就不贴出来了。下图是状态1,2,3在不同负载的情况下占总开关周期的比例:
在任何负载情况下,状态3的时间都是pi/wr/2,这个是保持不变的。在负载轻的时候,状态1和状态3主导开关周期,在完全没有负载的时候,状态2不存在,此时Vds呈正弦波。在负载比较重的时候,状态1和状态3所占的时间会急剧降低,此时状态2主导开关周期,Vds呈类似梯形或者矩形。另外变压器的次级电流的波形是三角波并且不连续(上面的等效初级电流Ipri也是这个波形),在整流桥后面滤波电容前面的电流波形和临界模式的反激变换器的次级电流基本一致。
如果这个功率电路改用它激定频驱动,其工作频率必须低于LrCr谐振频率而且两个驱动脉冲必须有一定共通,Q1Q2必须在状态4中完成换向,如果在其他状态换向会导致软开关失败。在定频驱动下,在一定负载范围内,变换器的次级电流与DCM的反激一致,输出负载特性也与DCM的反激一样,是恒功率源。
实际设计中的考虑
1. 变压器的设计,变压器设计是需要确保磁化电感不饱和的(只有磁化电感的磁路是在磁性材料里,而漏感的磁路在空气里所以漏感不会饱和哦),可以根据下式进行计算:
Ae是磁芯截面积单位平方米,Bsat单位特斯拉,是磁芯饱和的磁通密度,这个根据磁芯材料来,一般是0.1-0.25T之间,不推荐往死里艹,因为在启动一瞬间zvs是有超调的,这时候磁芯压力会比平时大一倍。ILr_pk是最大可能的峰值的电感电流,在最低负载电阻值时计算得到。计算得到的圈数是最少的初级圈数,注意的是这是初级两个绕组加起来的匝数,实际取比n大的一个偶数,然后中心抽头即可。最后在给磁芯中心柱开气息,调整到合适的电感量。变压器初级会过高频的AC,因此需要考虑趋肤效应。初级和次级推荐采用三明治绕法来降低漏感。
2.输入电感的选取
输入电感需要至少为3-4倍Lr大,其电流为有一定脉动的DC电流,但是AC成分很小,因此可以用单根粗线使劲绕,大力出奇迹。同样的,需要确保在大的DC电流下磁芯不会饱和,因此推荐使用铁粉芯磁环或者铁铝硅制作这个电感。
3.MOS管的选取
MOS管的耐压至少为pi倍的Vin(理论上空载时Vds最高的时候),这个在别的地方有证明。同时考虑到漏感带来的震荡,需要相应留有富余量。漏感带来的超压和负载大小呈正相关,上文介绍的方法在已知漏感的情况下可以比较准的估算最大MOS的耐压。如果不确定的话最好留有5倍输入电压的余量,比如12v输入,mos管最好选择75N75(75V)或者IRF540(100V)甚至IRFP250(200V)。
MOS管的峰值电流等于输入电流,其有效值为输入电流除以根号2。
4. 谐振电容的选取
电容的最大电压就是MOS的最大电压,大负载情况下电容的电流反而比轻载稍微少一点,因为有些电流被负载分流了,但是在状态1和3,电流的峰值依然很高。这个电容的要求就是要ESR内阻低,电磁炉电容还是首选,其实窝在考虑,用低内阻的贴片陶瓷电容也许可以胜任,但是价格或许更高了。
5. 特征阻抗的影响
增大Cr或者降低Lr会降低特征阻抗,在同样的谐振频率下带同样负载,低阻抗的LrCr组成的ZVS能输出更大功率。
6. 负载电阻最小能是多少?
细心的同学已经发现了,归一化的转换比Mnom在1到pi/2之间。pi/2对应的是空载,1对应的是临界极重载。当然实际中会有各种损耗,所以实际的停振增益会小于1一点。假设在极重载的时候,状态2的时间远比状态1和状态3长,则超重载频率只由状态2决定。此时可以推出fs=wr*Rn。然后带入Mnom=Mcritical=M/n,最后得到临界的Rn=(1-a*a)/4/a,然后就可以算出这个ZVS的最低负载电阻值。Mcritical取值在0.95到0.97左右就行,主要是一个估计损耗的情况。当然这个方法只能大致估计停振在何时发生。不要试图在靠近这个阻抗运行zvs,稍微不注意就会boom。
7.那推荐的负载点在哪?
负载(Po)增大会让变压器磁化电流(ILr)也增大,最终变压器会饱和。计算一下泥的变压器在这个圈数下的这个电感下的饱和电流,比它稍微小一点的磁化电流(ILr),对应的负载电阻,就是。
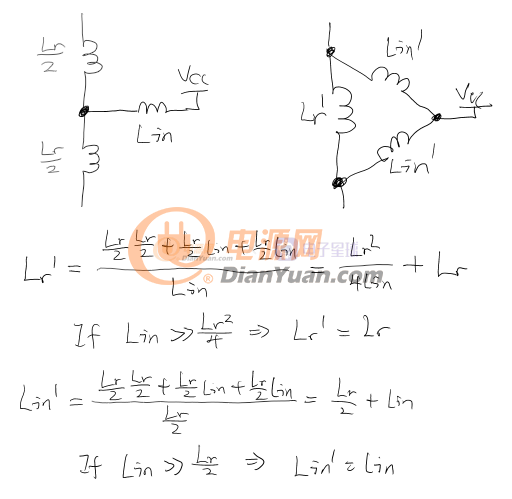
8.关于双电感无抽头的ZVS
把变压器初级的Lr分配到两个不耦合的电感上并假设输入电感大很多:
运用三jio画星星大法(delta to wye conversion)可以知道如果输入电感足够大(一般是这样的),那么yanli12321的双电感无抽头zvs和带抽头单电感zvs是差不多的。
更新
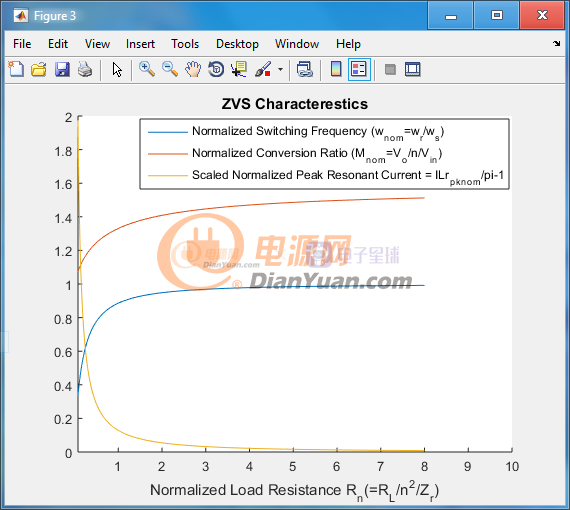
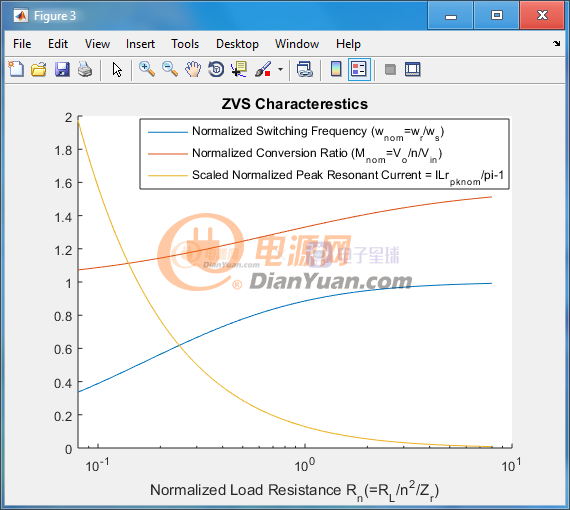
这次重新制作了ZVS特性图,加入了估算峰值磁化电流(也是谐振峰值电流)的曲线,三条曲线合在一张图中,后面的是x轴为指数的版本:
注意图中的黄线代表的归一化的峰值谐振电流是经过缩放和位移的,从图上根据Rn读数之后需要把读到的数先+1再整体乘以派,这个结果就是实际的ILr_pk_nom。计算峰值谐振电感的电流可以用ILr_pk=ILr_pk_nom*Vin/Zr来得到。
下面举一个例子说明如何用这个图表设计ZVS自激电路。需要提供:输入电压Vin,在最大负载时候的输出电压Vo,在最大负载时的负载等效电阻Ro和自然谐振频率fr,这个频率也是ZVS空载的开关频率。负载电阻Ro可以比实际的小一点,因为设计时考虑变换器是无损的。
首先选择ZVS的工作点,ZVS的工作点这里定义为Rn的大小,Rn同时决定开关频率,输出电压和峰值谐振电流(与变压器中的磁通量成正比)。一般取归一化谐振频率wnom=0.6左右时的Rn值,当然0.6也可以取稍微大点或者小点。Rn确定之后Mnom和ILr_nom的值都从图中确定了。然后带入公式计算出所有结果:
比较大的负载就需要比较小的Zr,但是小Zr会带来比较大的无功电流(Vin*pi/Zr,就是空载时候谐振电容的电流)。高fr需要较小的谐振电感和电容,但是Lr可能小到需要在变压器里加很大的气息,这样可能会增加漏感。
结束
如果有什么错误/疑问/需要补充的,请在下面指出哦w
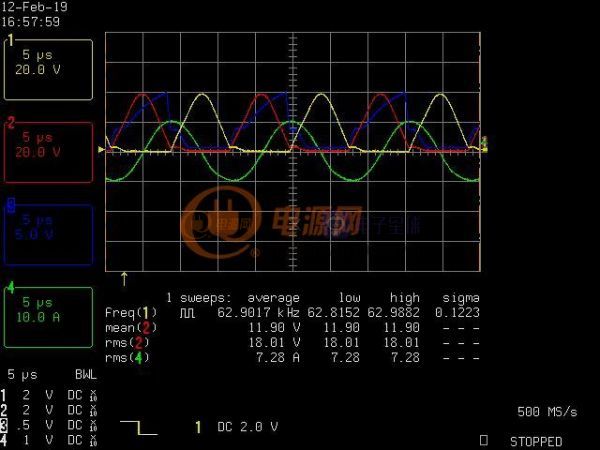
实验验证过程参见本贴5楼,非整流负载zvs的分析也在进行中(在另一帖更新)。