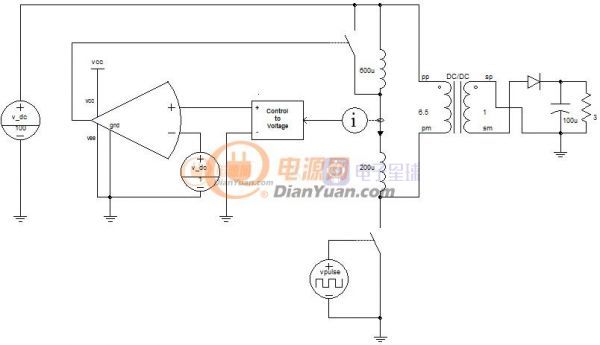
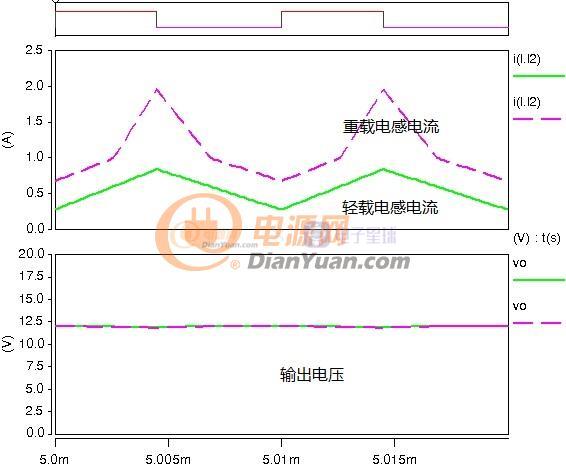
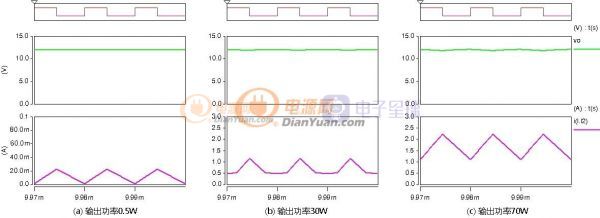
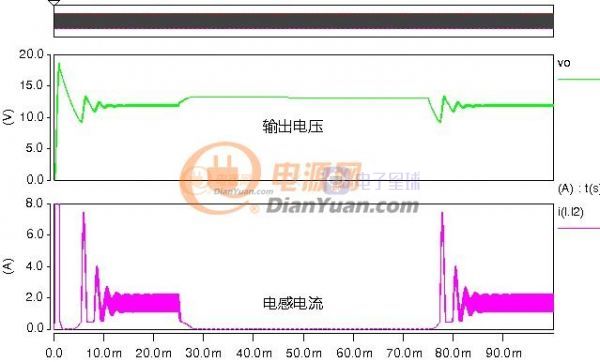
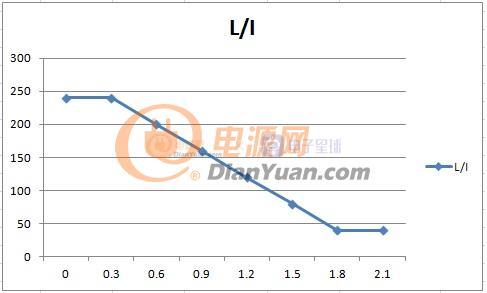
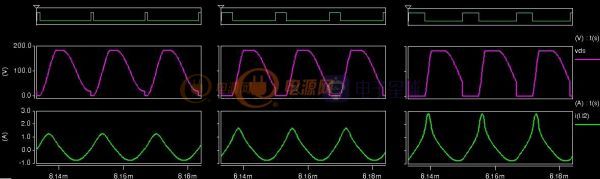
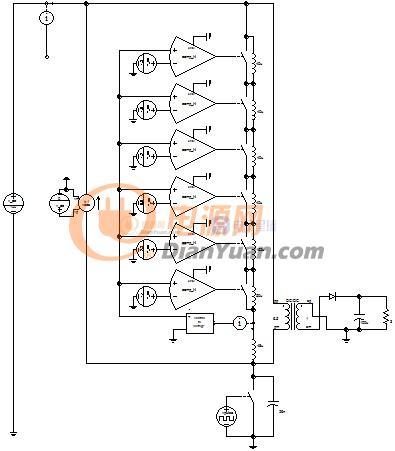
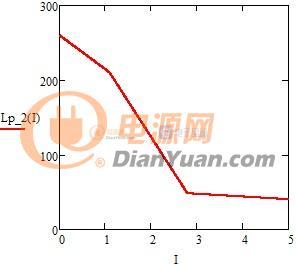
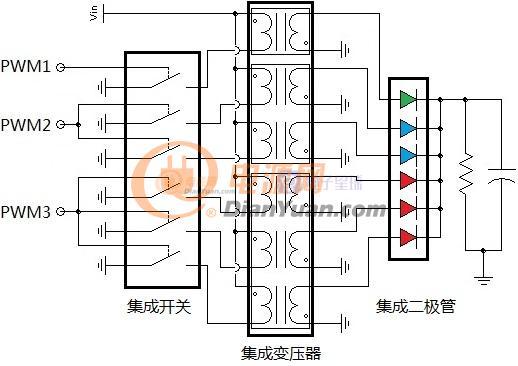
在几年前曾设想过一种可变电感,利用串联电感局部饱和来实现总感量的可变,如下:

图1-1 普通磁芯与非线性磁芯
昨天有幸听了陈为博士的讲座,这种非线性已经有实际应用了。
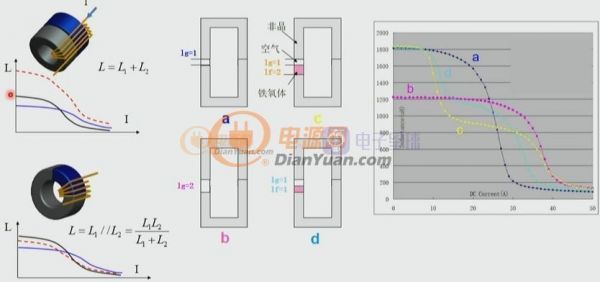
图1-2 不同磁芯串并联构成的非线性磁芯
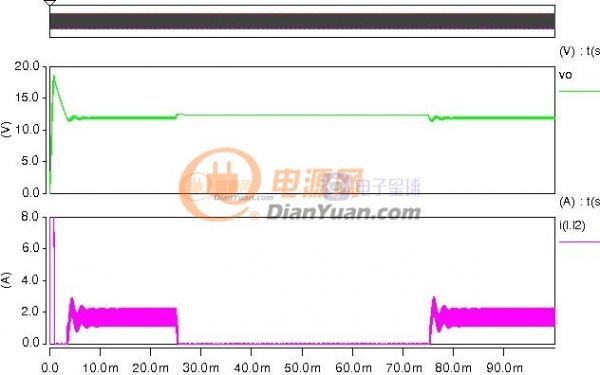
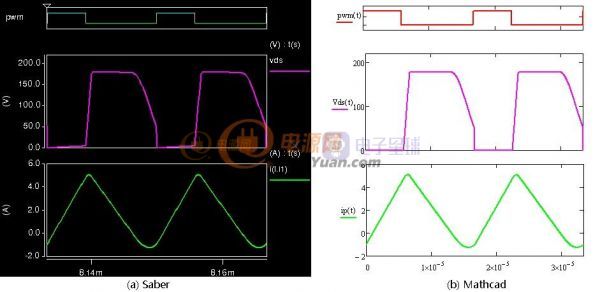
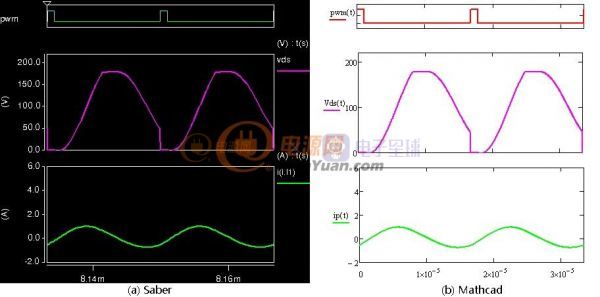
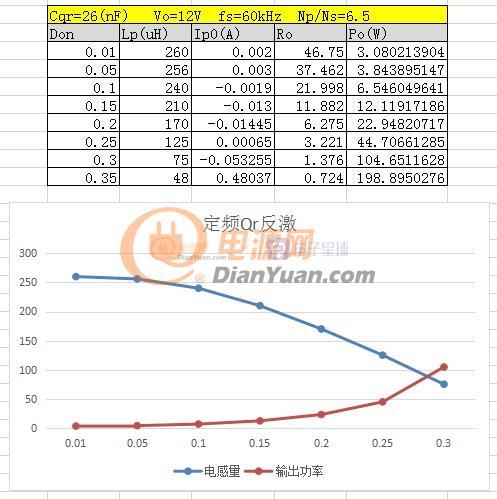
以反激电源设计为例,在相同开关频率下小功率反激的电感量一般设计的比较大,大功率反激的电感量一般设计的较小,当采用非线性磁芯后就可以兼顾大、小功率电源的优点。
再比如LLC电路,如果采用了非线性磁芯那么变频范围就可能缩小,有助于提高电路性能。
非线性磁芯的成本和工艺应当不是问题,在动态特性上可能会有些问题,本身开关电源就是非线性的现又增加了非线性的电感,那么在控制或环路补偿上可能会带来一些挑战。