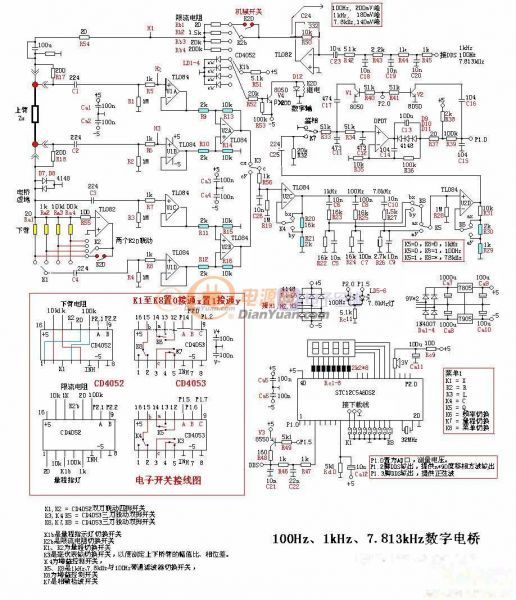
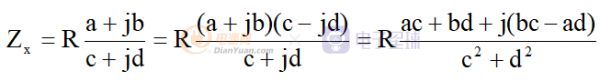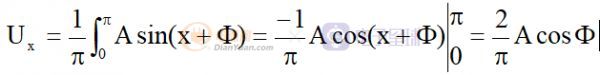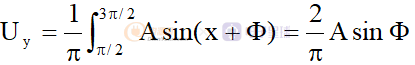LCR数字电桥的原理:
1、LCR电桥原理
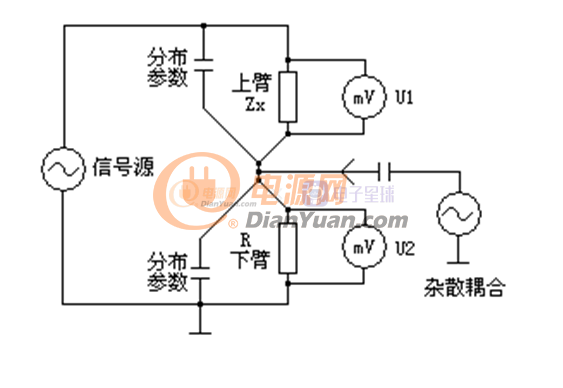
测定电抗元件Zx中电压U1与电流I,利用欧姆定律就可以得到 Zx=U1/I
当Zx串联了已知电阻R,那么测定了R上压降U2,就可得到Zx=U1/I
可见,无需测量I的具体值就可以得到Zx,这是电桥的一般特征。
为了得到Zx在x轴与y轴上的两个分量,以上计算须采用复数计算。
设U1= a+jb,U2=c+jd
那么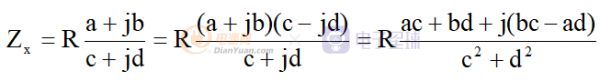
U1与U2要采用同一个坐标系来测量。借助相敏检波器,可以分离出a、b、c、d,相敏检波过程,需要一个稳定的0度与90度的正交坐标轴,测量期间,U1、U2向量也必须在这个坐标系中保持稳定,不能乱转。为了得到足够的精度,控制好放大器的增益,使得a、b、c、d的有效数字足够大,Zx的测量精度就高。然而,Zx分母两个正交量ac+bd和bc-ad,其中一个可能相对于另一个小得多,这就要求AD转换器的精度及分辨力要足够大,否则小的那一个难以分辨出来。
为了减小分布参数的影响,电路中引入了V/I变换器,上、下臂的中点变为了虚地。详见电路。
上、下臂电压分别通过“仪表三运放”缓冲放大后输出。“三运放”电路有较强的共模抑制能力。V/I变换器,并不能保证在7.8kHz时虚地对地电压为零,尤是在低阻测量时,这就产生了共模干扰信号,因此引入仪表三运放电路是必要的。可见,V/I变换器与“三运放”的结合,有效实现了上下臂电压的隔离放大,并且在音频域很容易得到高精度。
经K3切换上下臂,信号进入下一级放大。为了使电桥更精确,通常要求上、下臂使用“同一个毫伏表”放大(或者不放大,直接进行相敏检波)。由于本电路AD的分辨力不足,直接检波只能保证电桥在平衡点附近±30%的范围内取各较好的精度。如,桥平衡时对应表头字数600字,若被测阻抗不能使电桥平衡时,上臂变为600+300=900字,下臂变为600-300=300字,显然,对于300字的读数,最多只能得到0.3%的精度,超出这个范围后,精度将下降。以上分析表明,对于某一量程,保持良好精度的范围比较小,除非采用更高精度的AD。为了解决这个问题,后级可控增益对每个量程都启用,这样,各档测量范围就增加了,而精度没有明显减小。启用了可控增益放大器,上下臂电压测量实际上不再使用“同一个毫伏表”,因此误差大一点。
两级可控增加,分别为9倍和3倍,组合后,得到1、3、9、27四种增益放大。
电路中的杂散耦合总是存在的。没有严格的屏蔽,杂散耦合多少存在一点,对高阻测量有影响。当然,电路板内部信号传递过程中也存在一些杂散耦合,这种耦合干扰常表现为高、低阻测量总是存在理论预期之外的误差,适当的电路结构,可以增加抗干能力,必要时,还要在PCB板设计上多下点功夫。为了简化电路,采用了四运放电路,这也增加了运放之间的相互干扰。
带波滤波器的阻抗:带通滤波器可以抑制高频干扰,防止运放过载,同时可以减小工频干扰,使得末字跳动减小。此外,滤波器对高次谐波有一定的抑制作,对提高7.8k档D值精度是有一定帮助。设计滤波器应注意阻抗问题。高阻抗滤波器本身会受到电路板上的附加耦合的干扰。所以要求电容的取值不小于10nF
DDS滤波器的阻抗也不能设计得太小。道理与带通滤波器是一样的。即使是想设计100kHz的RC滤波器,也不宜采用小于10nF的电容。电路板上的分布耦合,可以按0.1pF至2pF之间估算。当后级信号比DDS信号大时,这种耦合是很可观的。如DDS输出0.2V,末级输出2V,那么0.2pF的耦合相当于0.2V下2pF的等效耦合量(类似密勒效应),当DDS滤波器输出电容采用1000pF时,那么2pF的附加耦合相当于引入了2/1000的0.2%的误差。倘若DDS输出滤波器的Q值较高,误差还要放大Q倍左右。实际上,在PCB布线中,没有进行充分屏蔽,10cm长度的引线,足以产生1pF的分布电容。布线长度,一般都有几个厘米或更长,加上元件本身有一定的体积,分布耦合还是比较大的。所以,使用1nF的滤波电容,产生0.2%的额外误差是很正常的。
由于LCR电路中,没有信号大电流,地线上也没有,所以对地线布置倒是没有很严格的要求。
2、V/I变换器的作用
为了更加准确的测量U1与U2,须满足一些测试条件。即流经被测电抗Zx的电流,必须严格等于流经电阻R的电流。
设Zx与R串联后,Zx另一端接信号源,R另一端接地。接信号源的那一端称为热端,接地的称为冷端,串联的连接点称为温端。现在有个麻烦的问题:当毫伏表接入Zx或R两端,会产生分流,引起Zx与R上的电流不会严格相同。再者,温端对地分布电容以及温端对热端的分布电容,也会造成Zx与R上的电流不相等。总体上说,会有一小部分电流从其它途径耦合到温端,结果Zx与R上的电流不相等。
当电路采用运放做“V/I变换器”,那么温端就变成了虚地。接在虑地上的对地负载电抗,不会产生分流,进而解决了毫伏表的分流影响。温端的对地分布电容,也可以看作对地负载。由于虚地对地电压为0,所以温端的对地分布电容不会分流Zx与R上的电流。
加入了V/I变换器,并不能解决温端与热端的分布电容耦合。切底解决这个问题的最好办法,就是对信号进行屏蔽。严格屏蔽,要用金属壳密封,广义屏蔽,就是信号源要远离Zx。
采用了V/I变换器,上臂热端、下臂热端,它们对地负载不会影响Zx、R上的电流。
如果不采用V/I变换器,电桥中点对地是浮动的,若想把U1、U2转换为对地电压,就须采用差动放大,而且要求差动三运方的共模抑制能力非常高,这不容易。采用了这种V/I变换器,对差动放大的共模抑制要求低一些。
有的LCR表设计,两臂电压测量直接采用开关切换,没有缓冲,这时上臂的限流电阻不可取值太大,以免切换过程中信号源电压变化,造成桥臂中的电流发生改变。当然,这种影响,也可以在软件中进行补偿。
·开关式鉴相器
正弦信号Asin(x+Φ),为了实现相敏检波,我们在信号通路上设置一个开关,使之仅导通半个周期。
导通开始时刻对x=0,那么导通期间的平均直流是: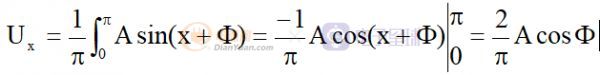
当导通时刻为x=π/2,平均直流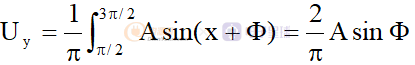
显然,如果使用复数表达,两个开关信号是相差90度的,构成坐标系。该正弦向量在这个坐标的辐角是Φ,模是A,它的两个正交量向量是实部(AcosΦ,0度)和虚部(AsinΦ,90度),而上面正交检波的结果与这两个向量的模值成正比,比例常数2/π。因此,对于一个理想开关,只要控制好开关的导通时序,确保Φ稳定,两轴严格相差90度,并且导通时间为1/2个周期,那么就可以分离出信号向量的两个正交分量。
实际相敏检波器电路的检波效率并不是上述的计算值K=2/π,而是K=(2/π)*2R/(4R+r),详见下图:
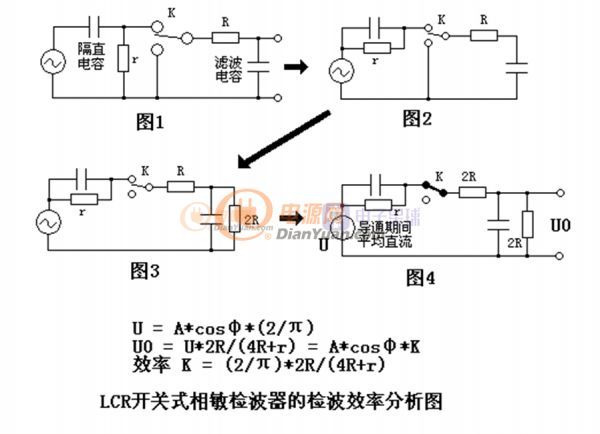
本电路的检波效率是:K=(2/π)*2R/(4R+r)=(2/3.14)*2*51/(4*51+20)=0.29