一全桥LLC闭环仿真,仅供参考。![]() LLC matlab
LLC matlab
针对全桥LLC拓扑,利用Matlab软件搭建模型,分别对轻载,满载进行仿真实验,对比使用增益曲线,以及matlab siulink搭建LLC模型的相关工作频率和输出电压关系,仅供参考。
案例1,输入Vin=275V,输出电压Vo=20V,谐振电感Lr=20uH,谐振电容Cr=88nF,励磁电感Lm=66uH,变压器匝比n=13,额定功率P=2kW。
一、LLC增益曲线
全桥LLC增益表达式(s域):

相关谐振电路参数定义如下:,特征阻抗,品质因数。其中等效负载。为实际负载。
画出LLC不同负载下增益曲线图:
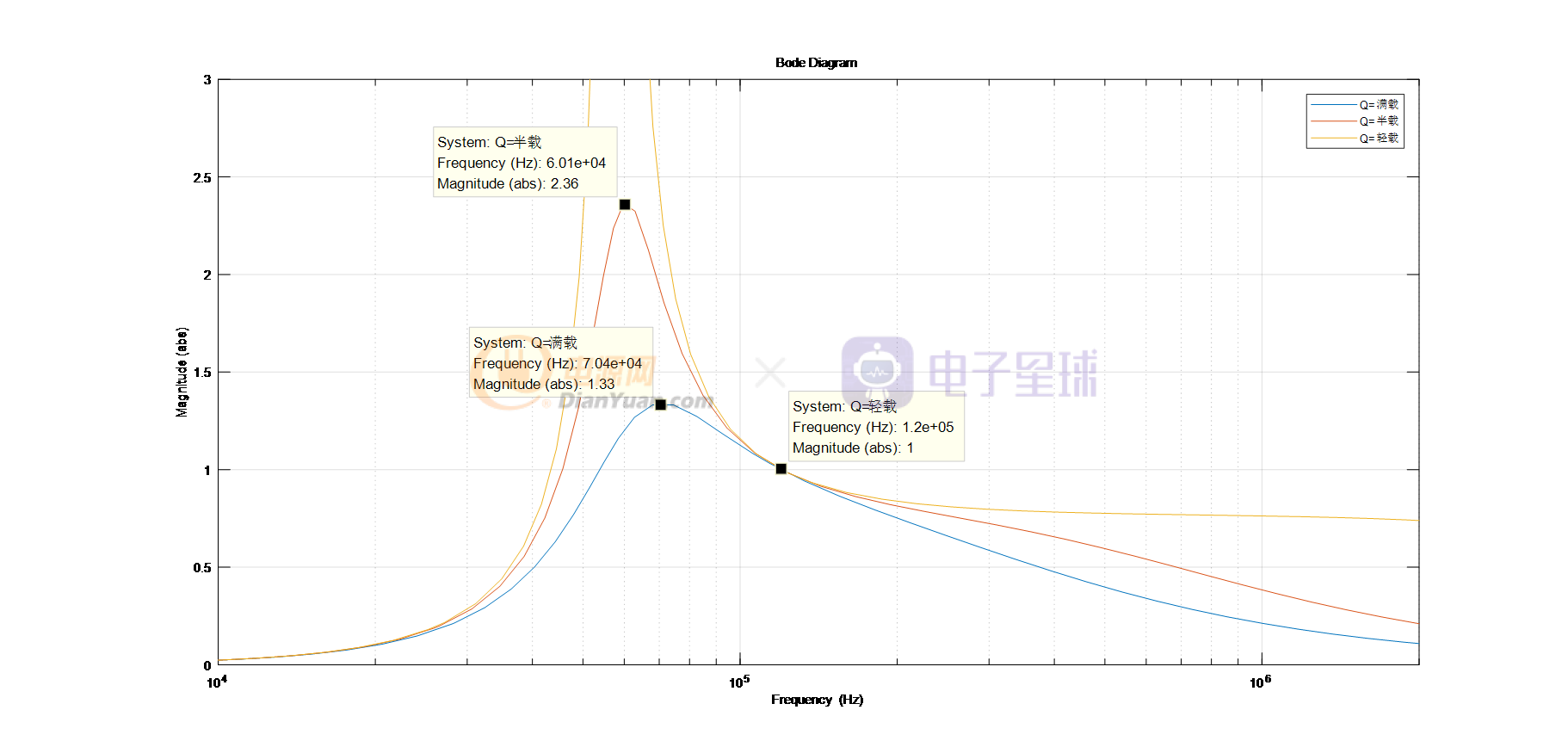
图1 LLC不同负载下增益曲线图
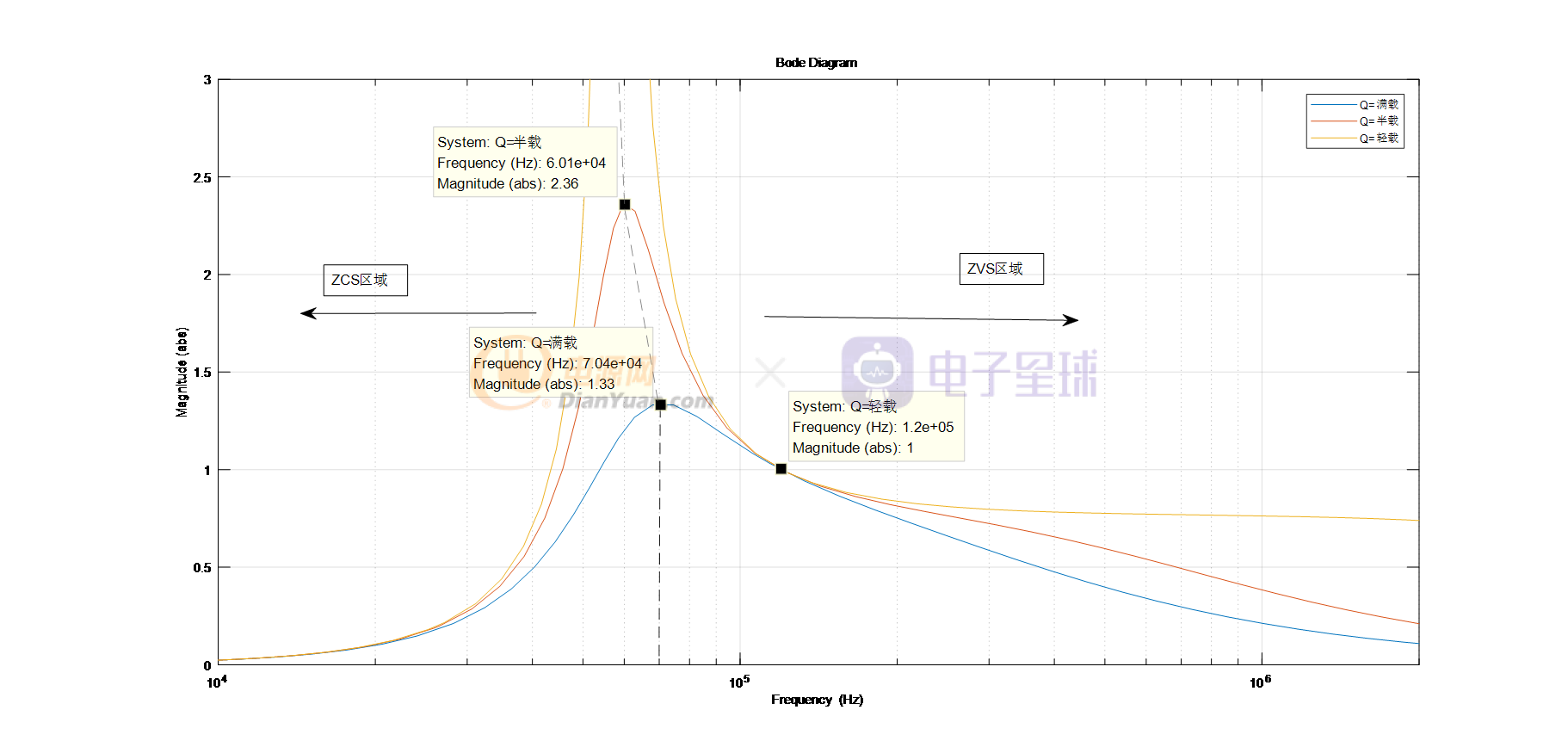
图2 LLC不同负载下ZVS以及ZCS划分示意图
图2中可见,在满载情况下,为了保持在ZVS区LLC最低工作频率大约在70.4kHz左右。
二、LLC仿真模型
于MATLAB中搭建全桥LLC仿真模型如下:
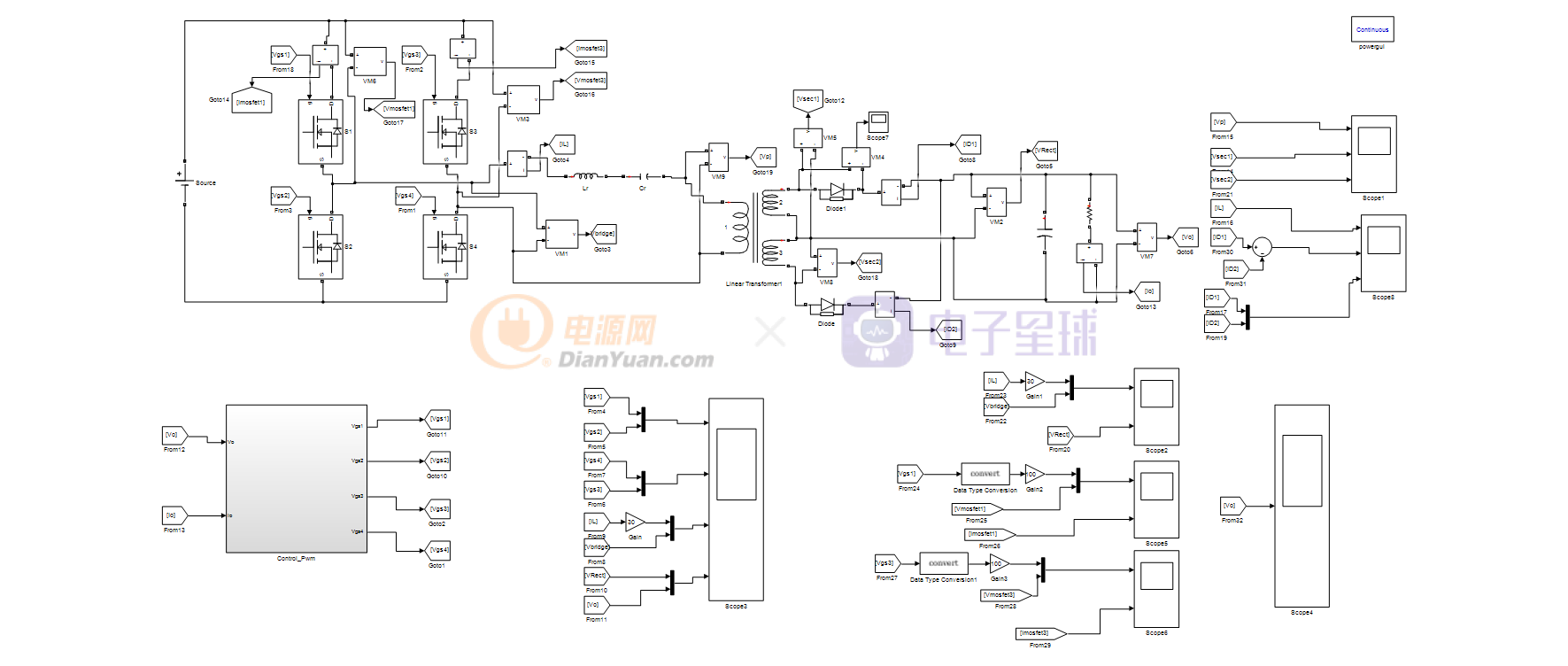
图3 全桥LLC仿真模型
控制部分设计,PI输出的物理意义是LLC的开关频率,最高设置为200kHZ,最低为80kHZ。软起动的时候LLC从低增益开始,实现电压软起动,所以PI的积分初始值设置为200kHZ,本仿真中是带载启动,为了加快软起,所以设置为150kHz。控制以及PWM产生模块如下:
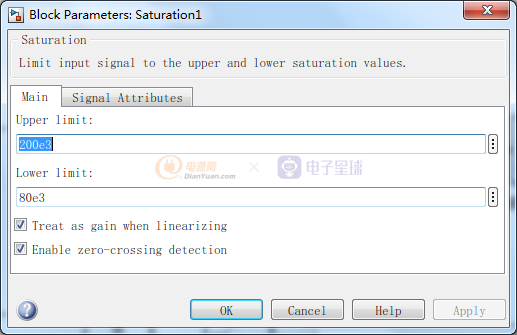
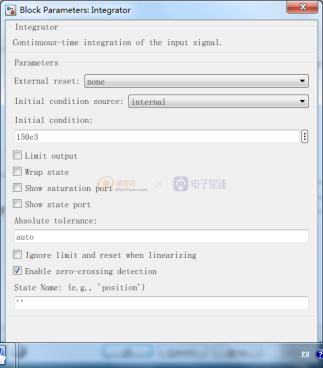

图4 全桥LLC控制部分
2.1 R=5轻载相关仿真波形
1)Vin=275V,R=5轻载谐振腔部分的仿真波形
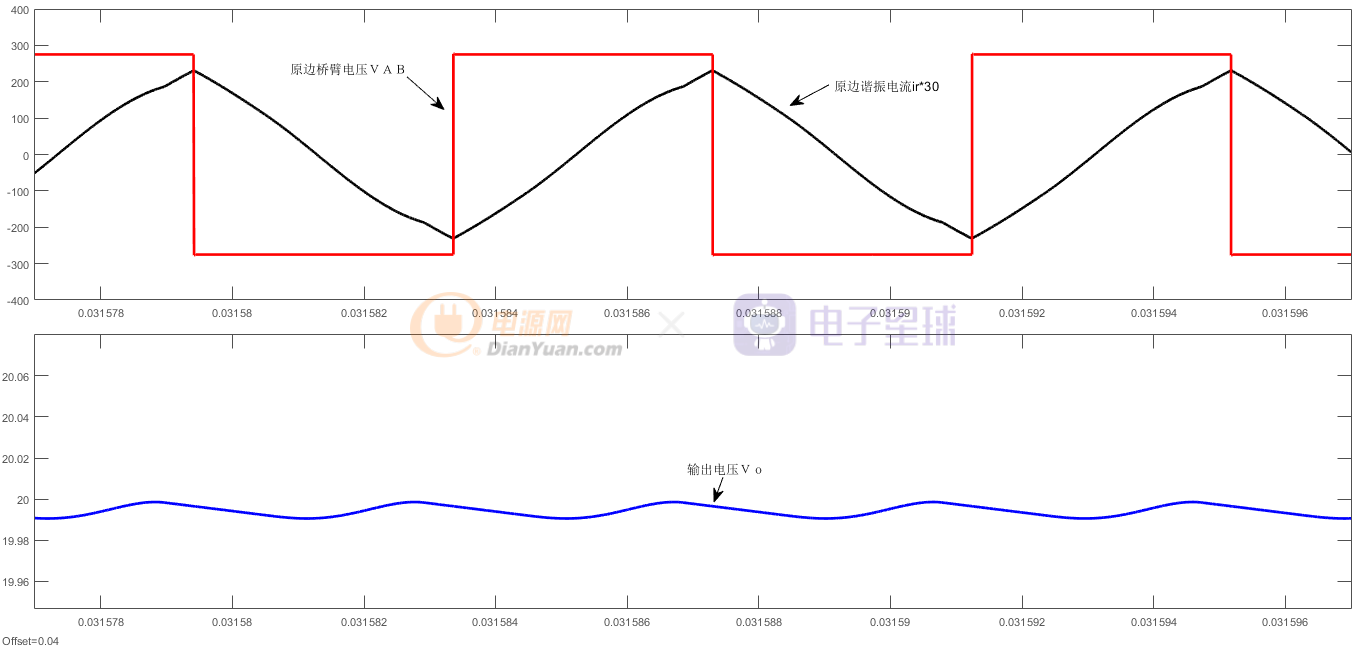
图5 R=5全桥LLC桥臂电压,谐振电流,以及输出电压
观察上图5可以发现,谐振电流ir滞后于原边桥臂电压VAB,可见谐振腔阻抗在当前开关频率下呈感性。
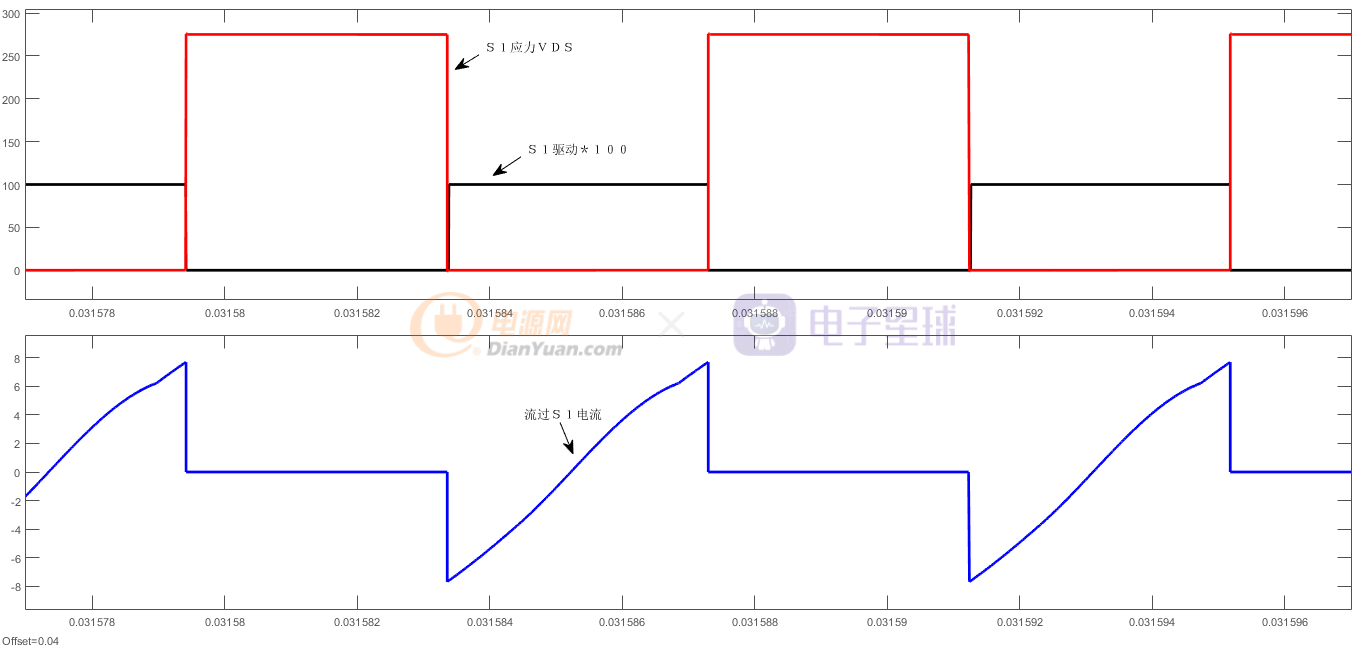
图6 R=5全桥LLC第一桥臂上管S1的应力,驱动,电流
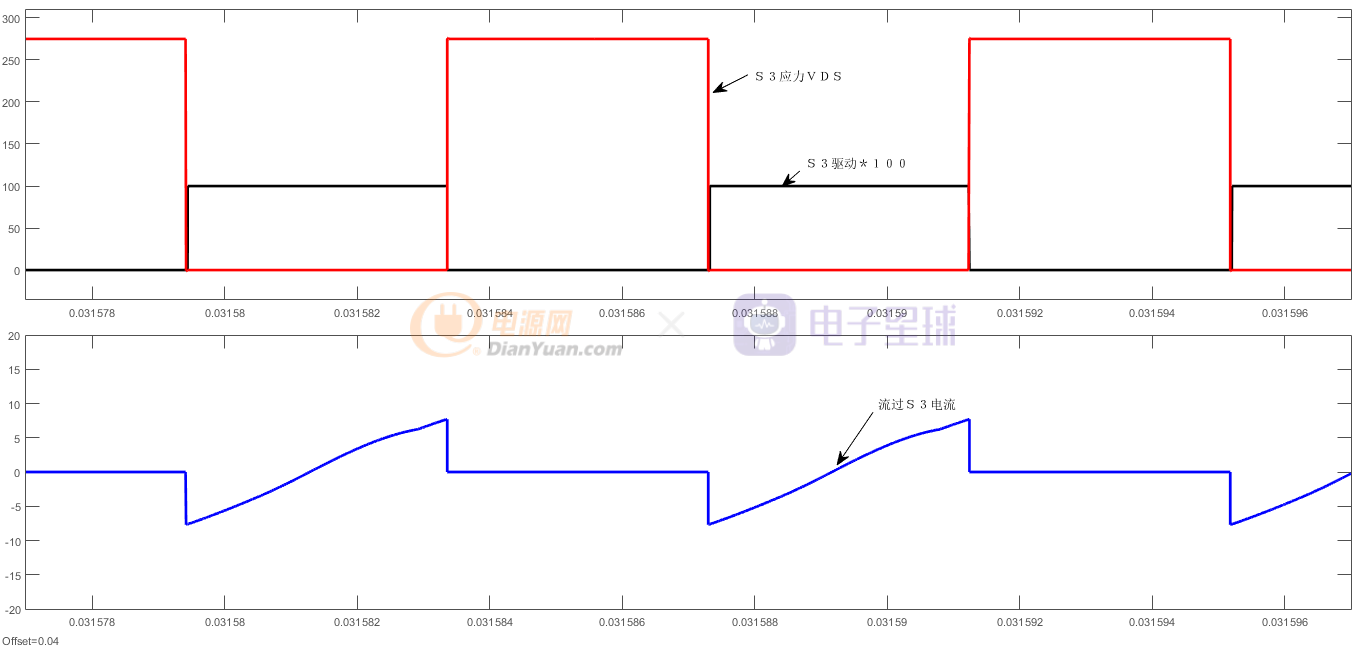
图7 R=5全桥LLC第二桥臂上管S3的应力,驱动,电流
由图6,图7观察S1,S3的VDS下降为0时,流过S1,S3的电流为负,可见开关管是在VDS下降为0而且对应管子的反并联二极管导通时开通的,因此它们都是零电压开通,而当它们关断时,其结电容的存在,使得它们是零电压关断。
2)R=5轻载输出整流侧相关波形
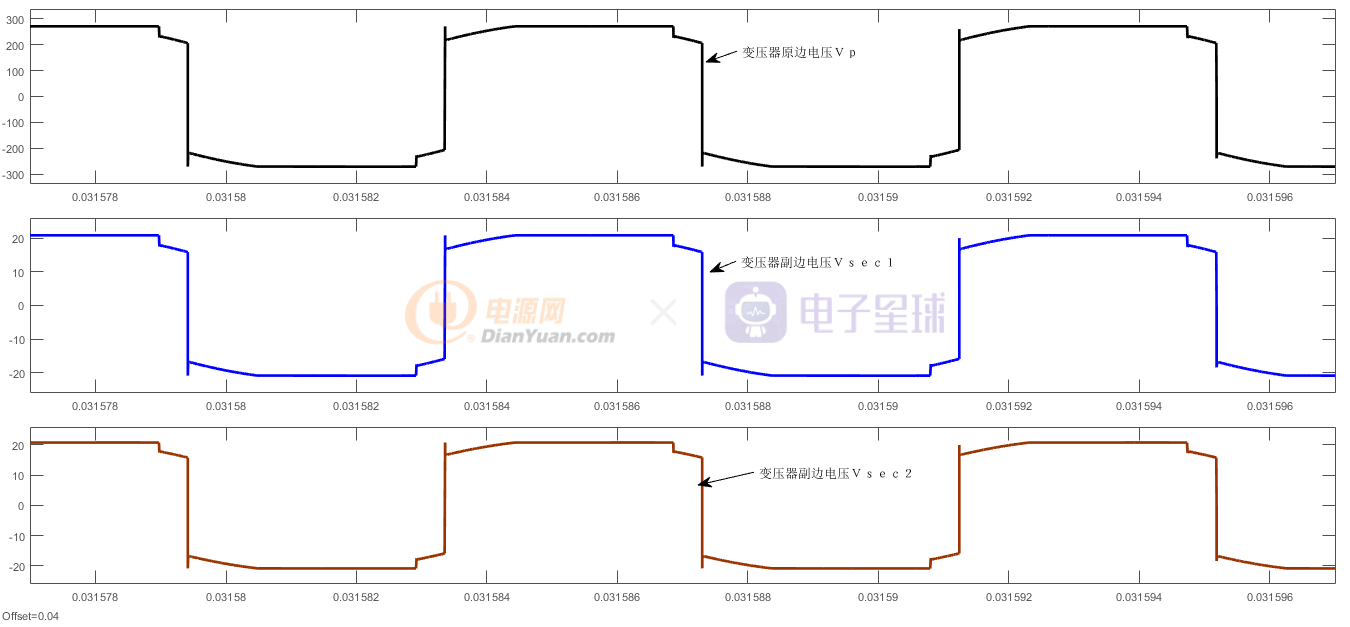
图8 R=5变压器原副边电压波形
观察图8可以发现,变压器原副边电压符合变压器基本规律,即:
Vsec1,2=Vp/n
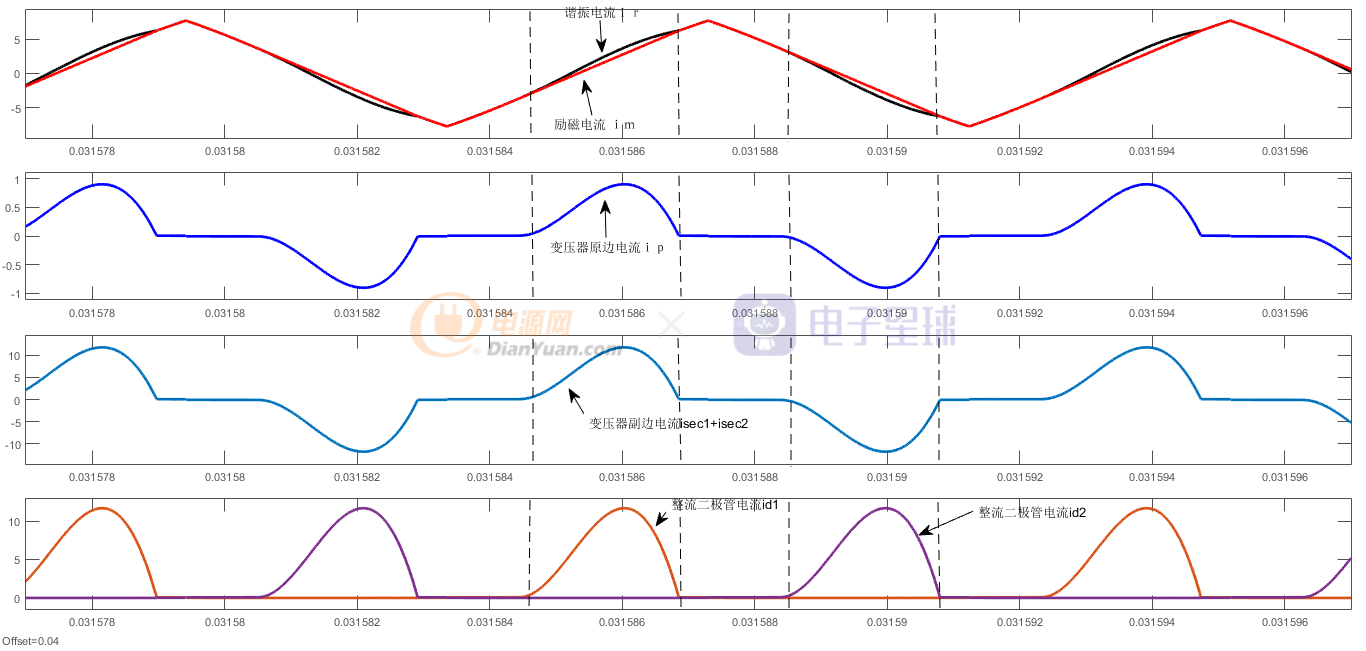
图9 R=5变压器原副边相关电流波形
观察图9可以发现,变压器原副边电流符合变压器基本规律,即:
isec1+isec2=n*ip
同时,在图9也可以发现,只有在谐振电流绝对值ir大于励磁电流im,才会有能量从原边传输到副边(图中画虚线部分)。虚线范围外,对应原边电流ip=0区域的能量将留在谐振腔体之内,这应该是影响效率的关键点之一。
3)根据增益曲线计算输出电压
对比增益曲线计算以及matlab仿真电压,观察matlab模型中在R= 5,最终输出Vo=20V时对应PI工作频率约为128.1Khz。
根据前面增益表达式,我们可以得到对应R=5的增益曲线:
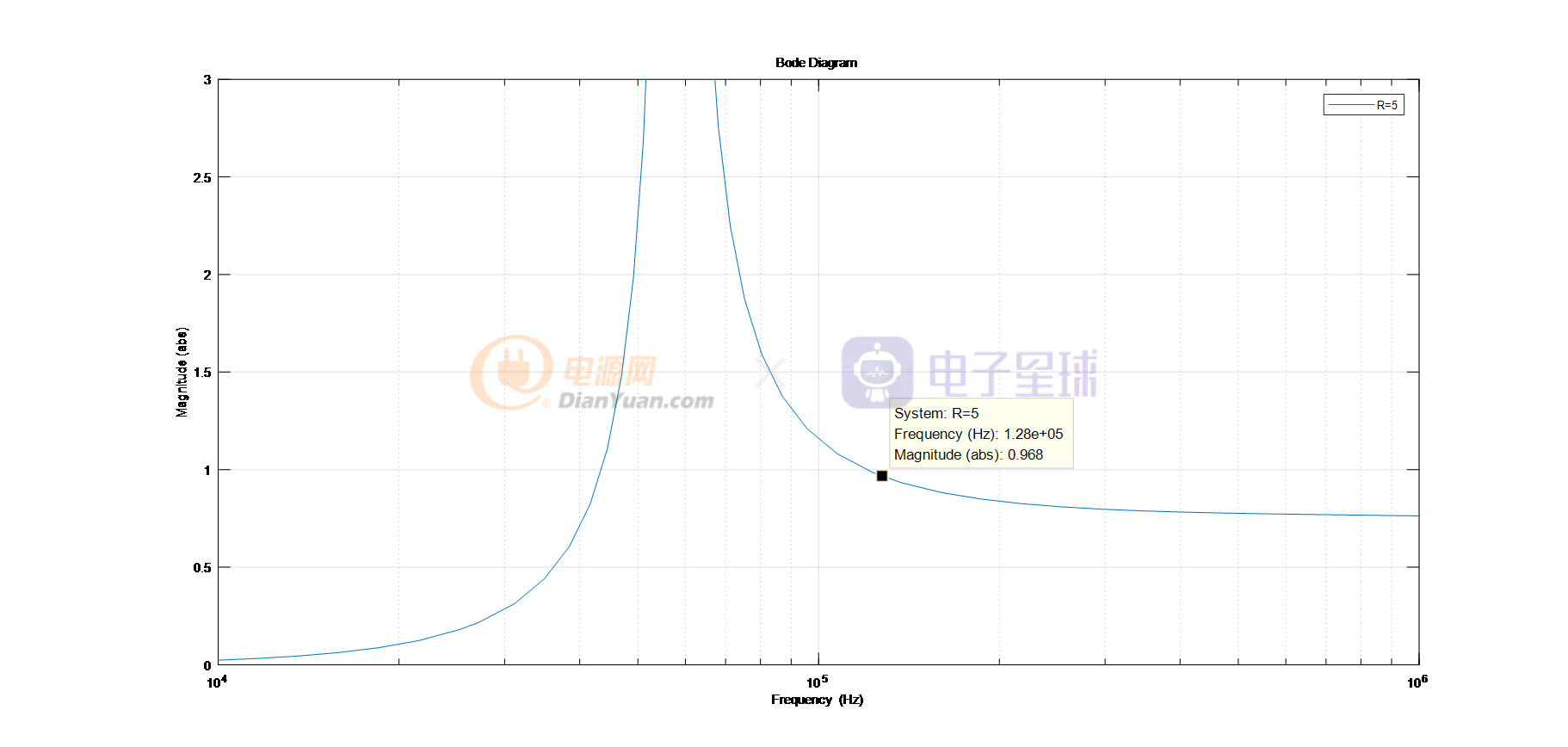
图11 matlab仿真模型R=5对应的增益曲线
已知Vin=275V,n=13,由上图中可知,在频率为128kHZ时,其增益M=0.968
根据:M=(n*Vo)/Vin
则:Vo=M*Vin/n= 20.47V
Matlab中输出电压平均值约为19.994V,PI工作闭环计算的工作频率约为128.1Khz与增益曲线计算结果基本保持一致。
如果输入电压变化范围为:225V至325V,输出20V,M=(n*Vo)/Vin则理论计算需要的增益分别为:1.1556,以及0.8。根据满载的增益曲线图12可知在输入电压为225V时,需要的工作频率为96.8k,在输入电压为325V时,工作频率为178kHz。
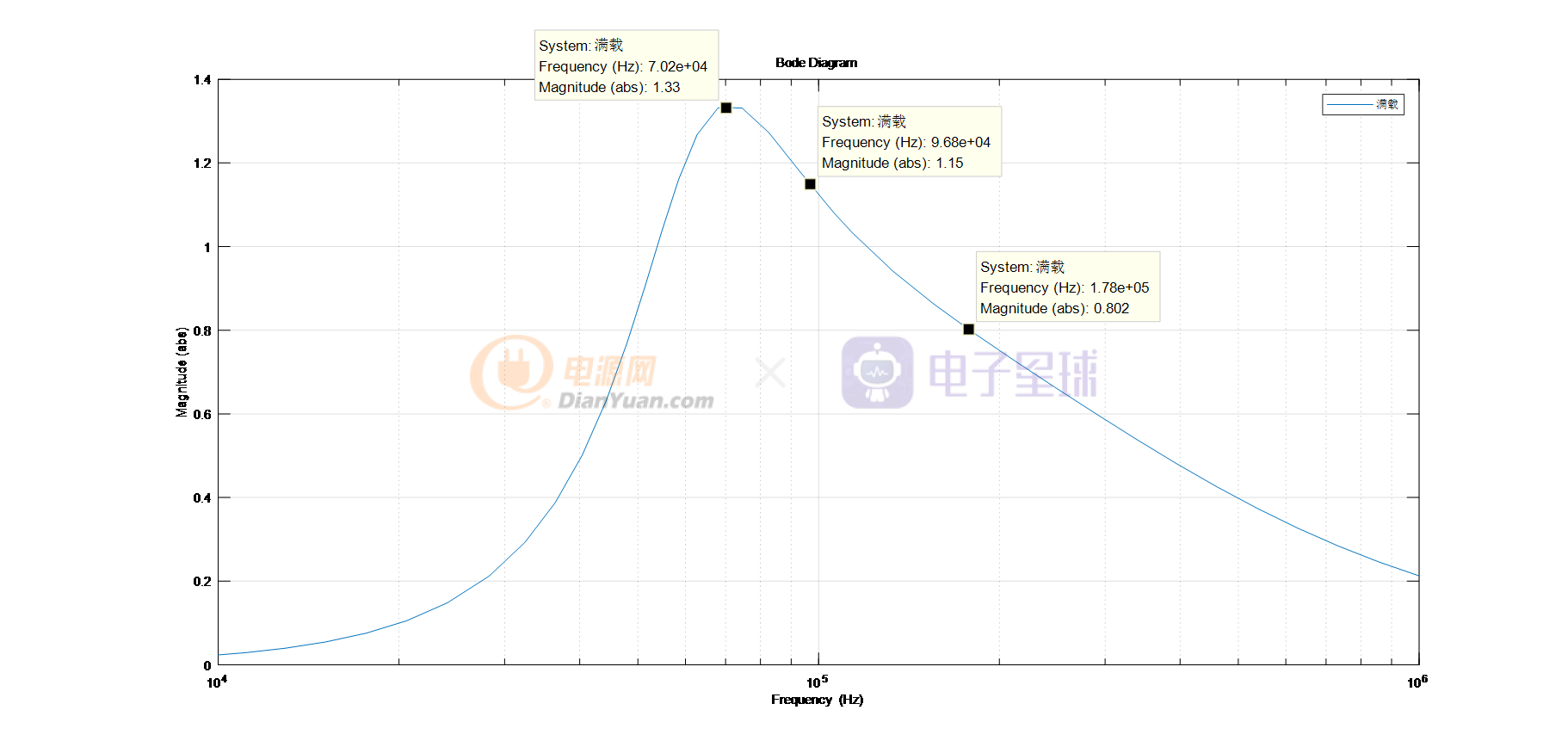
图12 matlab仿真模型R=0.2即满载对应的增益曲线
2.2 Vin=225V且R=0.2即满载相关仿真波形
1)Vin=225V ,R=0.2满载谐振腔部分的仿真波形
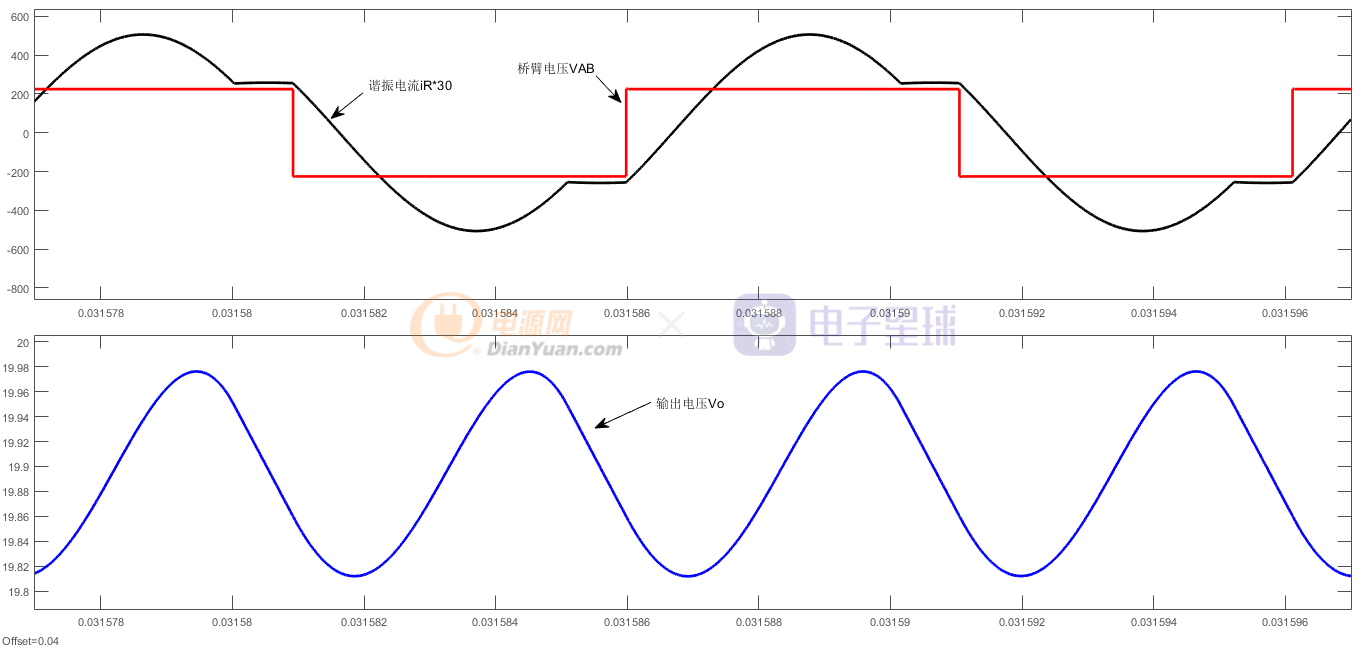
图13 Vin=225V,R=0.2全桥LLC桥臂电压,谐振电流,以及输出电压
由图13可知,此时VAB超前谐振电流,谐振腔在当前工作频率呈感性。
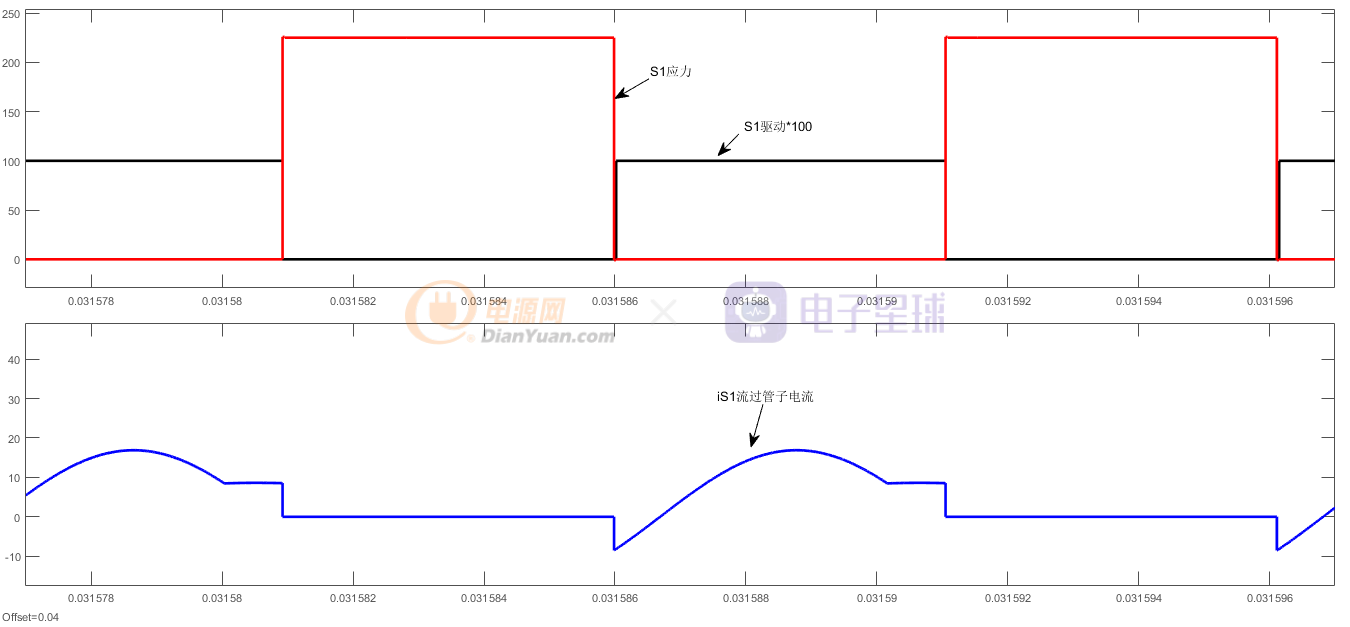
图14 Vin=225V,R=0.2,S1管子应力以及其驱动,电流波形
与R=5类似,如图14所示,S1的VDS下降为0时,流过S1的电流为负,可见开关管是在VDS下降为0而且对应管子的反并联二极管导通时开通的,因此S1是零电压开通,而当S1关断时,其结电容的存在,使得S1是零电压关断,其他管子驱动应力分析同理。
2)Vin=225V ,R=0.2输出侧波形

图15 Vin=225V,R=0.2,变压器原副边电压波形
观察图15同样可以发现,变压器原副边电压符合变压器基本规律,即:
Vsec1,2=Vp/n
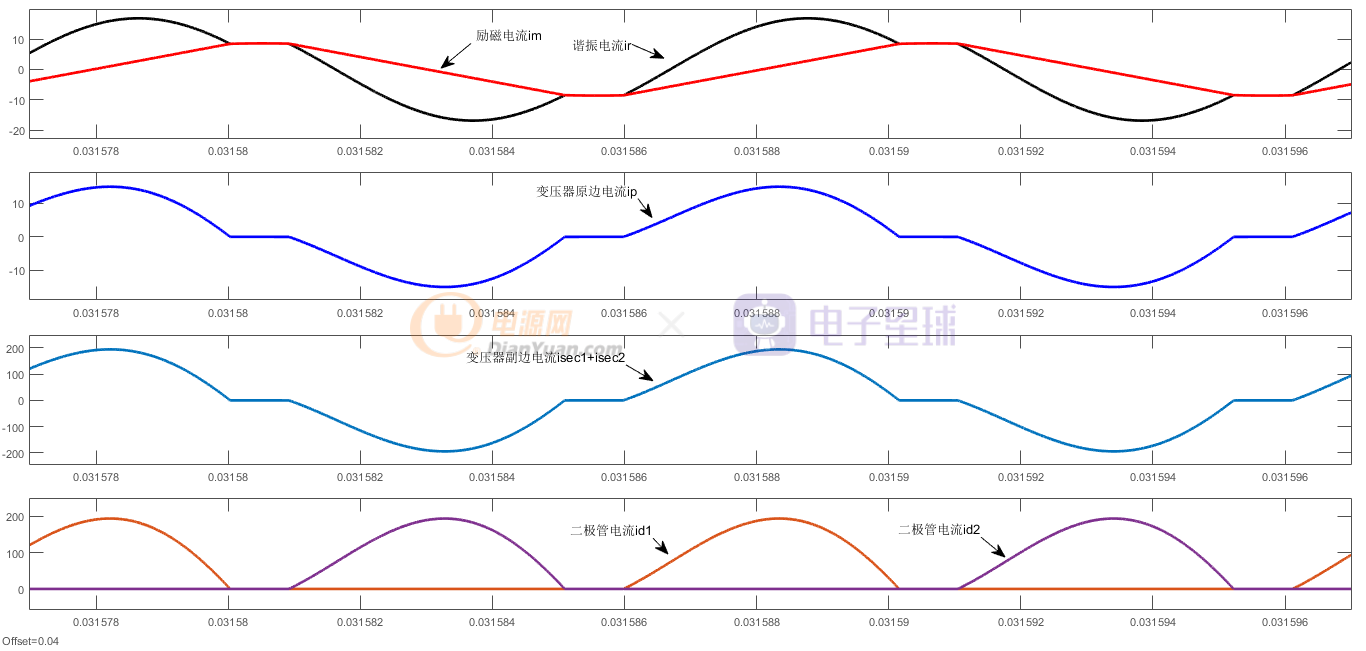
图16 Vin=225V,R=0.2,整流侧电流以及原边对应
由图16变压器原副边电流符合变压器基本规律,即:
isec1+isec2=n*ip
在图16也可以发现,只有在谐振电流绝对值ir大于励磁电流im,才会有能量从原边传输到副边,对应原边电流ip=0区域的能量将留在谐振腔体之内,同时由图16可知副边二极管是零电流开关。
在Vin=225V,R=0.2时,控制环路PI输出的工作频率约为99.1kHz,与图12增益曲线对应的96.8k大体一致。

2.2 Vin=325V且R=0.2即满载相关仿真计算
Vin=325V且R=0.2即满载相关仿真(波形略),观察控制环路PI输出的工作频率约为151.6kHz左右。与图12增益曲线得到的178k相差较大。
综合Vin=225V,325V,满载R=0.2,结合图12满载增益曲线图得到下表一:
表一 满载时增益曲线以及matlab仿真数据对比
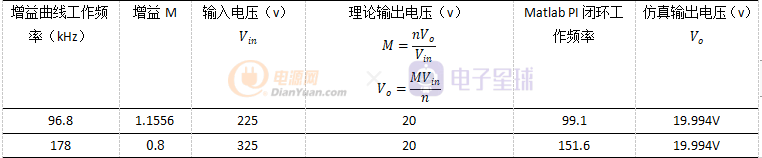
注: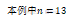
可见,matlab仿真闭环的频率与增益曲线所计算的工作频率有所出入,而且在频率高的时候,出入偏得更多,原因是增益曲线求取是基于基波近似的,必然存在误差,而该误差与所在工作频率也存在一定关系。同时matlab仿真模型的元件均为理想元件,所以跟实际项目依旧是必然存在误差的。
三、结语
通过matlab,计算LLC增益曲线,以及Matlab搭建模型,方便分析LLC的相关波形,后续可根据实际项目继续补充。
附:llc仿真模型(直接复制,matlabR2016b之后版本均可打开):
matlab附增益曲线计算m函数源代码:
Lr=20e-6;
Lm=66e-6;
n=13;
Cr=88e-9;
w0=1/sqrt(Lr*Cr);
f0=w0/2/pi
wp=1/sqrt((Lr+Lm)*Cr);
fp=wp/2/pi
% R=pi^2*sqrt(Lr/Cr)/8/2
R=20^2/2000;
Re=8*R*n^2/pi^2;
Q=sqrt(Lr/Cr)/Re
Hs=tf([Re*Lm 0 0],[Lr*Lm Re*Lm+Re*Lr Lm/Cr Re/Cr]);
% R=pi^2*sqrt(Lr/Cr)/8/1
R=20^2/1000;
Re=8*R*n^2/pi^2;
Q=sqrt(Lr/Cr)/Re
Hs1=tf([Re*Lm 0 0],[Lr*Lm Re*Lm+Re*Lr Lm/Cr Re/Cr]);
R=5;
Re=8*R*n^2/pi^2;
Q=sqrt(Lr/Cr)/Re
Hs2=tf([Re*Lm 0 0],[Lr*Lm Re*Lm+Re*Lr Lm/Cr Re/Cr]);
P1 = bodeoptions;
P1.FreqUnits = 'Hz';
P1.Grid = 'on';
P1.Xlim={[1e4,1e6]};
bodemag(Hs,P1);
% hold on;
% bodemag(Hs1,P1);
% bodemag(Hs2,P1);
legend('满载');
matlab计算llc增益方法二
Lm=66e-6;
Lr=20e-6;
Cr=88e-9;
Np=13;
Ns=1;
Uo=20;
Io=100;
K=Lm/Lr;
fr=1/(2*pi*(Lr*Cr)^0.5);
fs=1/(2*pi*((Lr+Lm)*Cr)^0.5);
Rac=Uo/Io*8/pi^2*(Np/Ns)^2;
Q=2*pi*fr*Lr/Rac;
Uo=20;
Io=50;
Rac=Uo/Io*8/pi^2*(Np/Ns)^2;
Q1=2*pi*fr*Lr/Rac;
Uo=20;
Io=4;
Rac=Uo/Io*8/pi^2*(Np/Ns)^2;
Q2=2*pi*fr*Lr/Rac;
X=0.01:0.01:2;
for num=1:1:length(X)
G(num)=K*X(num)^2/(((1+K)*X(num)^2-1)^2+(Q*K*X(num)*(X(num)^2-1))^2)^0.5;
G1(num)=K*X(num)^2/(((1+K)*X(num)^2-1)^2+(Q1*K*X(num)*(X(num)^2-1))^2)^0.5;
G2(num)=K*X(num)^2/(((1+K)*X(num)^2-1)^2+(Q2*K*X(num)*(X(num)^2-1))^2)^0.5;
X(num)=X(num)*fr/1000;
end
% [Gmax Gindex]=max(G);
axes1=axes();
plot(X,G,'b');
hold on;
plot(X,G1,'r');
plot(X,G2,'y');
grid on;


