PWM可以算是数字电路中的“独臂”神通,“独臂” - 只需一根线;“神通” - 在很多关键的应用中起到栋梁的作用。PWM(脉宽调制 Pulse Width Modulation)从字面意思上讲它是一种“调制”方式,调制就意味着在某些载波信号上携带了某些的信息,通过解调的过程就可以得到其携带的信息,这些信息的属性由PWM的产生端定义,总之在这一根仅仅发生0、1交替变化的信号线上可以做出很多文章。
今天我们就看看如何通过PWM的方式实现数字到模拟变换的功能,也就是通过改变一根管脚的输出脉冲,得到模拟世界的某种波形。
首先PWM是由一串连续行走在某输出管脚上的0、1交替出现的信号组成,我们称高电平1为ON,低电平0为OFF,ON+OFF为一个周期T,ON的持续时间除以周期T就为占空比 - Duty Cycle,看下面的两个图。
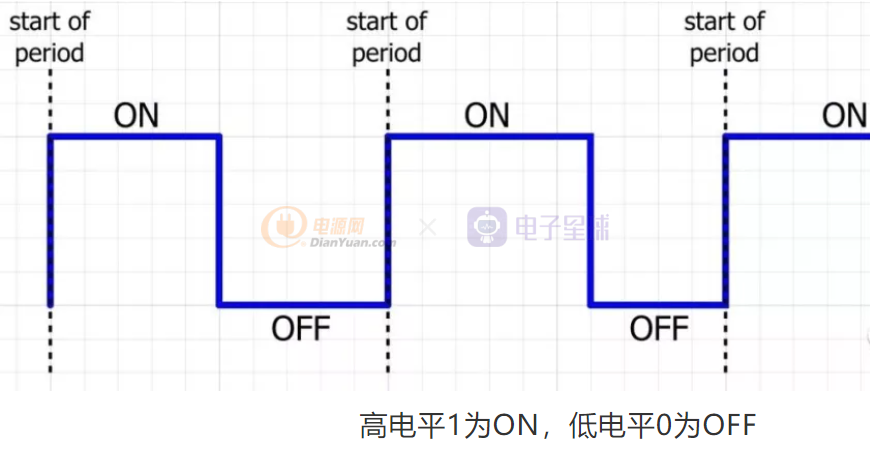

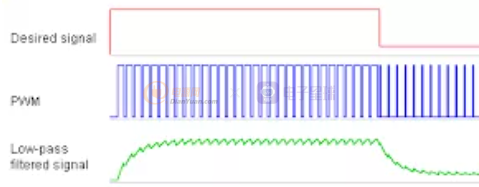
如果发送端用脉冲的占空比来传递“电压值”,也就是将某个数字的电压值对脉冲的占空比进行调制,就可以在接收端通过RC低通滤波器(也就是解调器)从调制脉宽的数据流中得到需要的模拟电压值,从而达到DAC的目的。看下面的动图 - 假设脉冲的占空比为0的时候(整个周期全部为OFF - 低电平)代表电压值为0,占空比为100%的时候(整个周期全部为ON - 高电平)代表电压值为最高电压,比如3.3V,则40%的占空比就是40%*3.3V。占空比改变-每个周期的脉宽改变,也就意味着输出的电压值在改变。

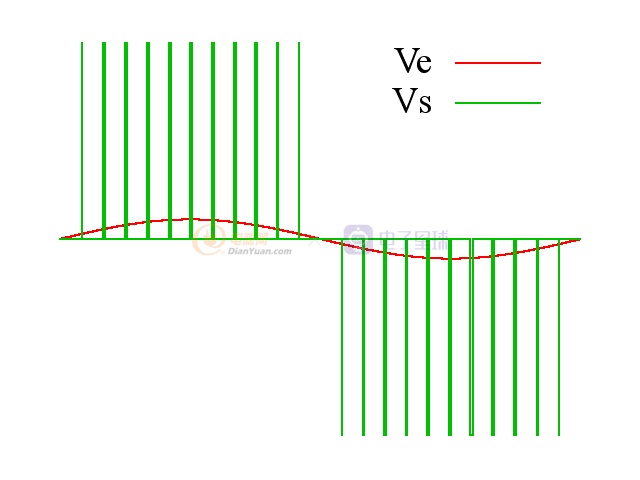
用脉宽的改变携带电压值的变化信息
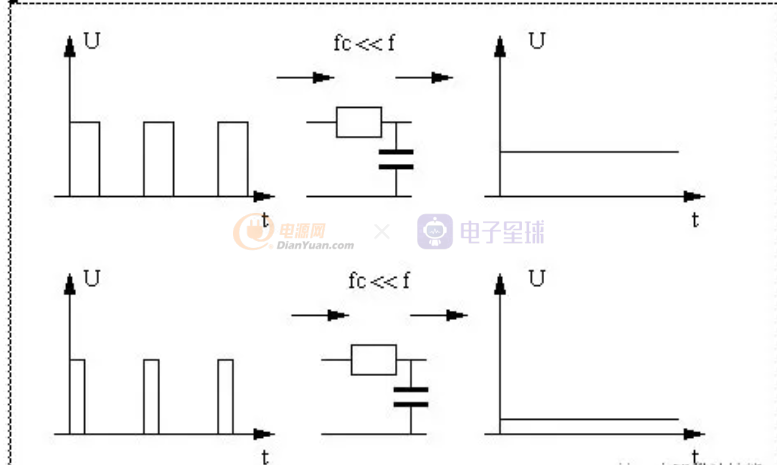
用一个电阻和电容组成的低通滤波就可以将PWM中携带的电压信息“解调”成模拟的电压值
前面讲过DAC的两个关键指标 - 转换率和转换精度,在PWM里是如何对应的这两个指标么?
看一下下面的波形:
PWM-DAC的转换频率相当于脉冲的重复频率
PWM-DAC的分辨率相当于脉冲宽度相对于整个周期的精度,举例如果一个最小的脉冲ON的时间为5ns(可以用100MHz的时钟计数产生),PWM脉冲的周期为5ns x 256 = 1.28us,则这个PWM-DAC相当于是8位的DAC。
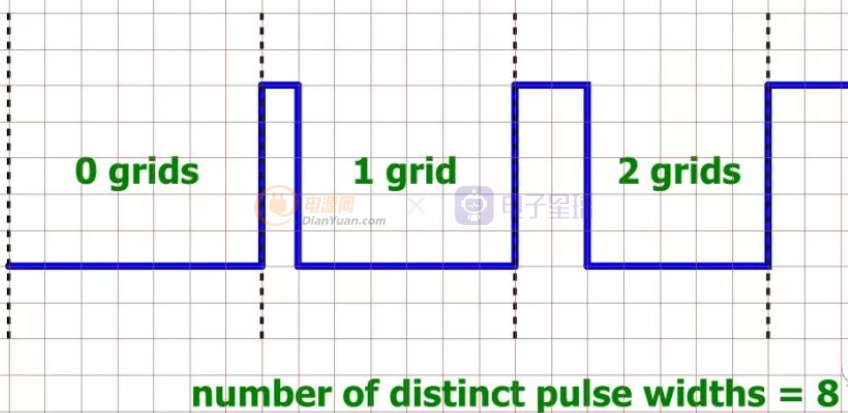
也就是说如果你用100MHz的时钟来通过PWM的方式做一个8位的DAC,最高的转换频率也只能到1/1.28us ~ 781KHz分辨率高则转换率降低,因此用PWM做的DAC一般用于生成非常低频的信号乃至直流信号。
下面的图为经过一个最简单的由一个电阻R和一个电容C构成的低通滤波以后得到的模拟信号,可以看到在输出的模拟信号上还是有很高频率的纹波。
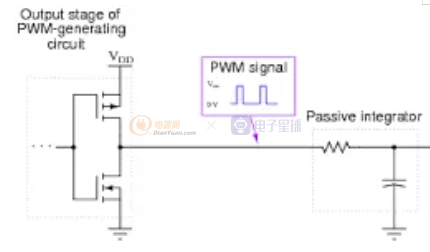
如果要进一步平滑输出模拟信号上的波纹,可以通过加入电感或着用运算放大器构成的有源低通滤波器来对纹波实现更强的抑制。
是不是很简单?只需一个R和一个C就能得到你想生成的模拟信号,做一个简单的任意波形发生器很简单啊。
有的朋友会问,很多MCU内部都有DAC啊,干嘛不用内部的DAC?
苏老师答:如果有的话自然不需要折腾PWM了,如果没有,只需要一根管脚和俩器件就能实现这样的功能还是很有用的,再说了,也许你的系统中需要多个DAC的功能,而你的MCU内部没有足够的DAC,且你也不想或者没有足够的管脚外挂一个单独的DAC器件(需要I2C或SPI总线连接),PWM方式是个非常不错的选择哦。
如果你用的是FPGA或CPLD,里面根本没有DAC,而你又需要一个,拿出一个管脚来产生PWM就会非常666。
理解用PWM生成DAC的机制、局限,在关键的时候也许就能起到意料不到的结果。
最好的方式是直接动手试试喽 - 在一个小脚丫的输出管脚上加上R和C,用计数器生成以下PWM信号,用示波器看看你能得到什么。
首先我们看一下脉冲信号的频谱,根据傅立叶变换,周期为T的脉冲信号可以分解为多个单频率的信号的叠加,最小的频率分量为1/T,有兴趣的可以通过Matlab自己做一下分析。
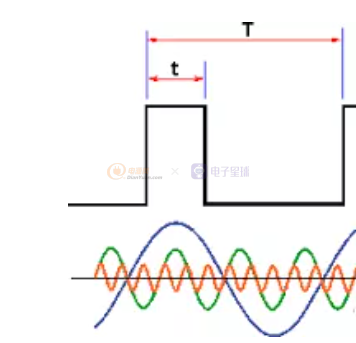
比如,我们对幅度为3.3V、周期为10uS(频率100KHz)、占空比为50%的脉冲信号(此时为方波)进行FFT变换,可以得到1.65V的直流分量、100KHz、300KHz(3次谐波)、500KHz(5次谐波)。。。等频率分量,最小的交流频率为100KHz。
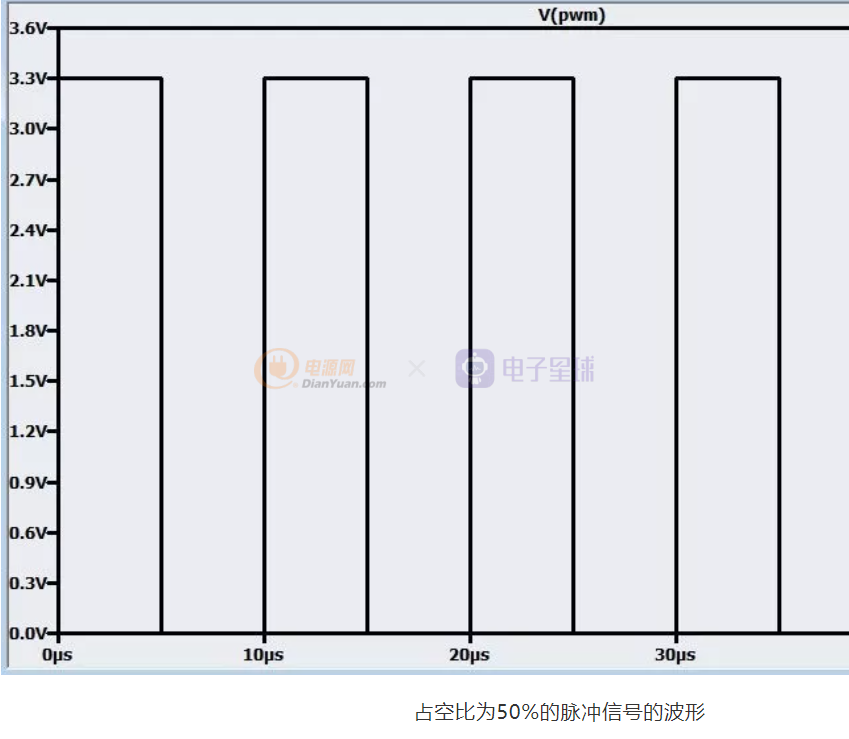

从以上简单的分析可以看出,无论占空比是多少,脉冲波形除了直流分量以外,交流部分的最低频率都为脉冲的重复频率100KHz上,在DC和脉冲重复频率100KHz之间一马平川,光秃秃的。
因此,如果要得到直流分量,只需要去掉100KHz以上的频谱能量就可以了。最简单的方法就是通过由一个电阻R和一个电容C构成的一阶低通滤波器,其截止频率为fc=1/2*Pi*R*C,我们要得到的是直流分量,滤除的是100KHz以上的频率,因此只要截止频率在100KHz以内,并且能对100KHz以上的所有频谱都有较好的抑制,就能够得到比较好的DC输出。
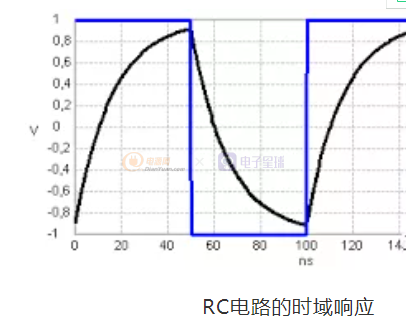
可以想象,截止频率越高,越是接近要滤除的频率(比如50KHz之于100KHz),该滤波器对100KHz的滤波效果就较差,就会有一定量的残余能量出现在滤波器的输出端,如下图,也就是输出的波形纹波比较高。
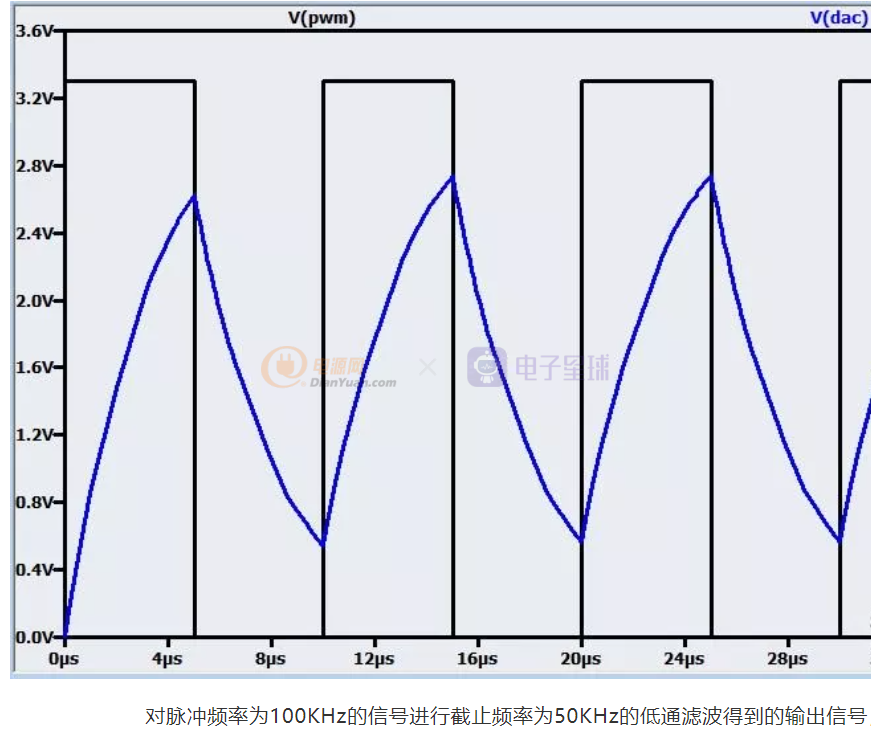
如果降低截止频率,越是接近直流,从而距离要滤除的频率越远,比如针对100KHz的脉冲频率选择1KHz作为LPF的截止频率,则在100KHz处可以达到非常高的抑制度,100KHz的残留就非常小,也就是在输出的直流信号上的纹波可以变得很小,如下图

但却出现了另外一个问题 - 需要花费很久的时间(学名叫建立时间 setting time)才能达到应该达到的DAC的直流值。原因就是fc低,意味着RC更高,也就是充电的时间常数变得很长 - R增大意味着对C进行充电的电流变小,要对C冲电到一定的值花费的时间也就更久。,
因此这就出现了一个让人纠结的选择:
选择较低的截止频率 - 较低的纹波,较长的建立时间
选择较高的截止频率 - 较大的纹波,较快的建立时间
你会说一阶不够,要不多用几阶滤波器,加上电感或者有源的运放来进行低通滤波,这确实能改善滤波的效果,但 -- 电路的复杂度增加、元器件成本增加了,且改善有限。
那不增加电路的复杂程度,还是只用这一个R和一个C是否能够改善性能呢?
答案是肯定的,其实也很简单 - 把交流分量的频率踢的远远的,在保持较低的时间常数(建立时间短)的情况下,将LPF的截止频率fc和要滤除的脉冲重复频率之间的间隔尽可能的拉开,比如将100KHz的重复频率给踢到10MHz(出去100倍),占空比不变,如果用原来的50KHz的滤波器,到了10MHz的地方怎么也把10MHz以上的频率给消灭的只剩下一点渣了。看下图,直流建立时间大约为15µs, 纹波变得只有25mV左右了。
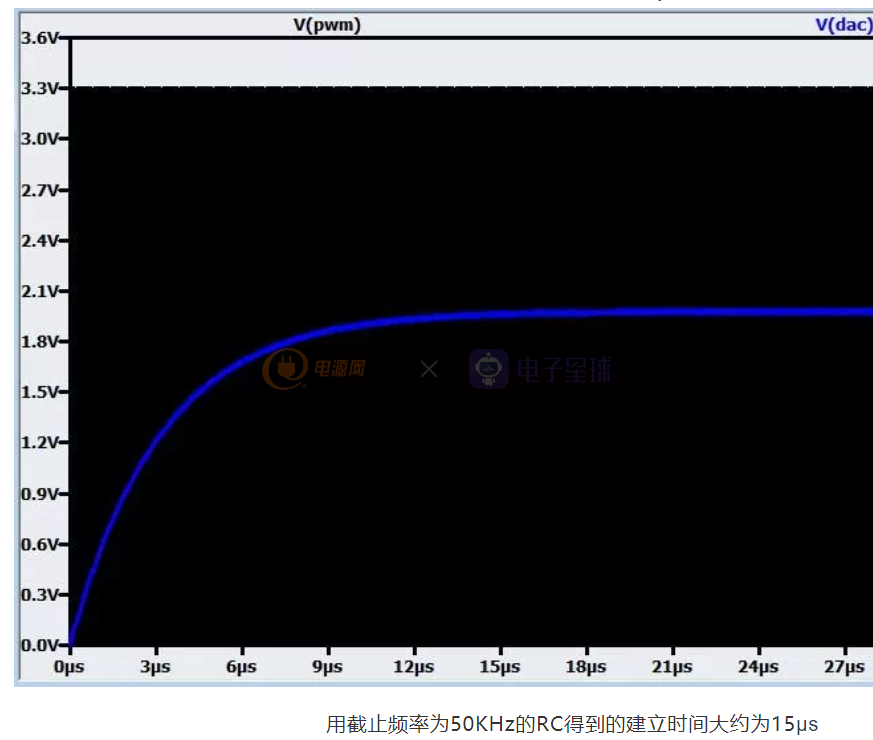
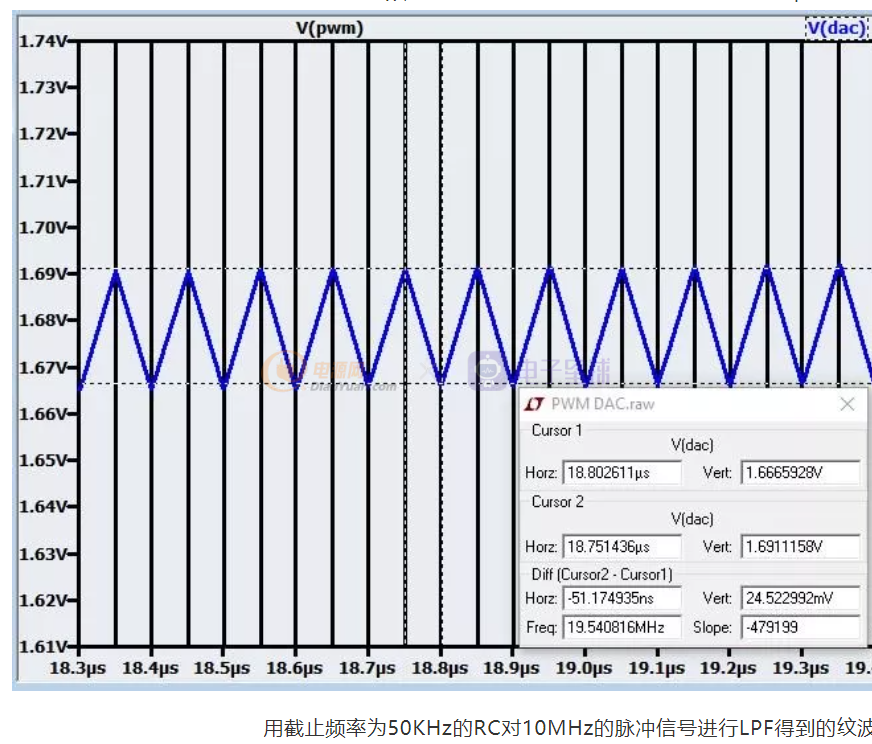
是不是很神奇?其实理论依据很简单,自己把低通滤波器的频响曲线画一下就很容易理解了。
到这里我们就应该知道如何设计自己的PWM系统的各项参数来构造一个简单好用的DAC。

