大家好,很高兴和各位一起分享我的第三十二篇原创文章,喜欢和支持我的工程师,一定记得给我点赞,收藏,分享哟。想和我进一步探讨技术干货,可以添加微信号(matlab_simulink)。
对称分量法是分析不对称故障的常用方法,根据对称分量法,一组不对称的三相量可以分解为正序、负序和零序的三相对称分量,将电网等效为各分量下的等效序网络后,就可以对电力系统的各种不对称运行及不对称故障情况进行分析。但是,传统的对称分量法定义在频域范围,用相量表示,在进行对称分量分析时,需要计算各个相量的模值和相位,故只能应用于电力系统不对称运行或不对称故障的稳态分析中,而无法应用于系统的暂态分析。
而在电力电子装置控制系统设计过程中,对暂态不对称运行或者不对称故障分析格外重要(比如SVG、HVDC等),我们需要各个分量的瞬时值,利用电压或电流的瞬时值构造相应的无延时旋转相量,再利用这些旋转相量进行对称分量变换,获取各个序分量的瞬时值。
在三相电路中,对于任意一组不对称的三相相量(电压或电流),可以分解为三组三相对称的相量,当选择a相作为基准相时,三相电流相量与其对称分量之间的关系(以电流为例)为
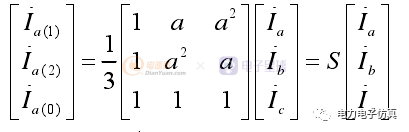
(1)
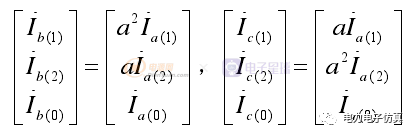
(2)
令三相不对称电流的瞬时值为
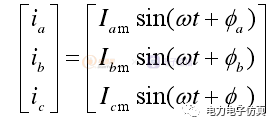
(3)
式中,Ia,Ib,Ic分别表示三相电流的瞬时值;Iam,Ibm,Icm分别表示三相电流的幅值;φa,φb,φc分别表示三相电流的初相位。
设与三相电流Ia,Ib,Ic所对应的旋转相量分别为

(4)
由上式可知,旋转相量的虚部的系数就是三相电流的瞬时值,只要求出这些相量的实部就可以确定这些向量。而相量实部的求取可以根据三角函数的关系式,可以求导法完成。
分别对三相电流求导可得
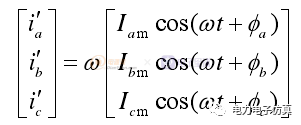
(5)
三相电流的导数是对应旋转相量实部的ω倍,由此,可以利用导数构造三相电流的旋转相量。在实际工程的应用中,求导可以在离散数字量的基础上用差分方法完成,即
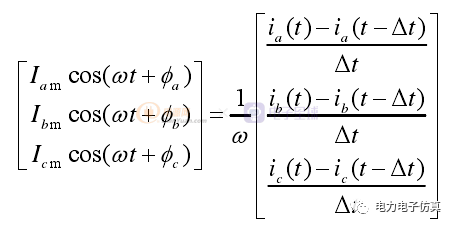
(6)
式中, Δt为计算步长,ia(t),ib(t) ,ic(t) 分别为三相电流的当前步长的瞬时值;ia(t-Δt),ib(t-Δt) ,ic(t-Δt)分别为上一步长三相电流的瞬时值。
基于所构造的旋转相量,将式4代入式1和2,经过整理可分别得到三相电量的正序、负序和零序分量的瞬时值:

整体控制框图为:
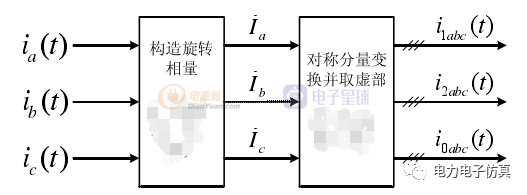
为了验证上述方法可行性,在simulink搭建一个简单的三相不对称电路,电网电压为380V,三相负载分别为:1Ω+2mH,2Ω+2mH,1Ω+1mH,三角接法。对其电流进行分析,仿真结果如下 :
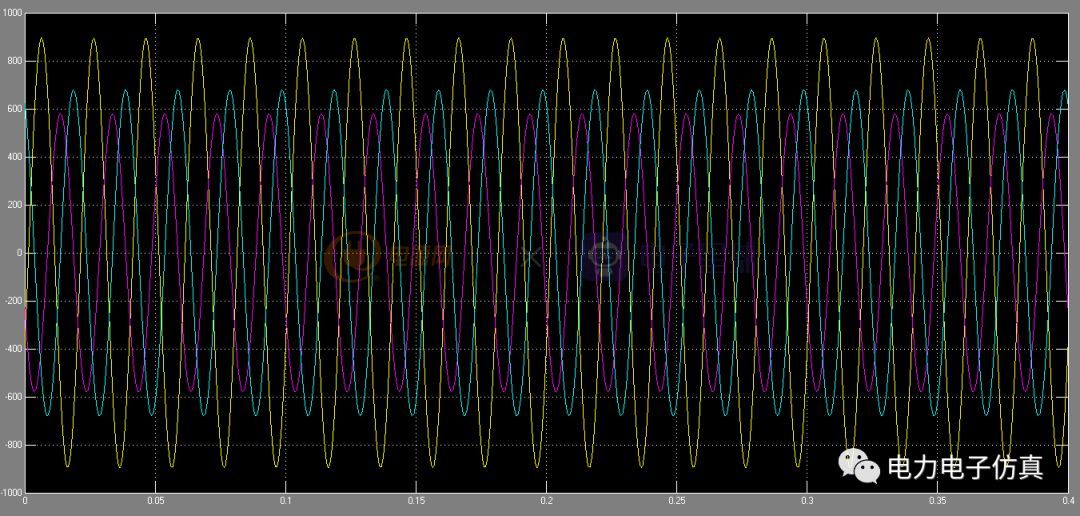
上图为电网电路,从仿真结果可以看出,由于三相负载不对称,故三相电流不对称。
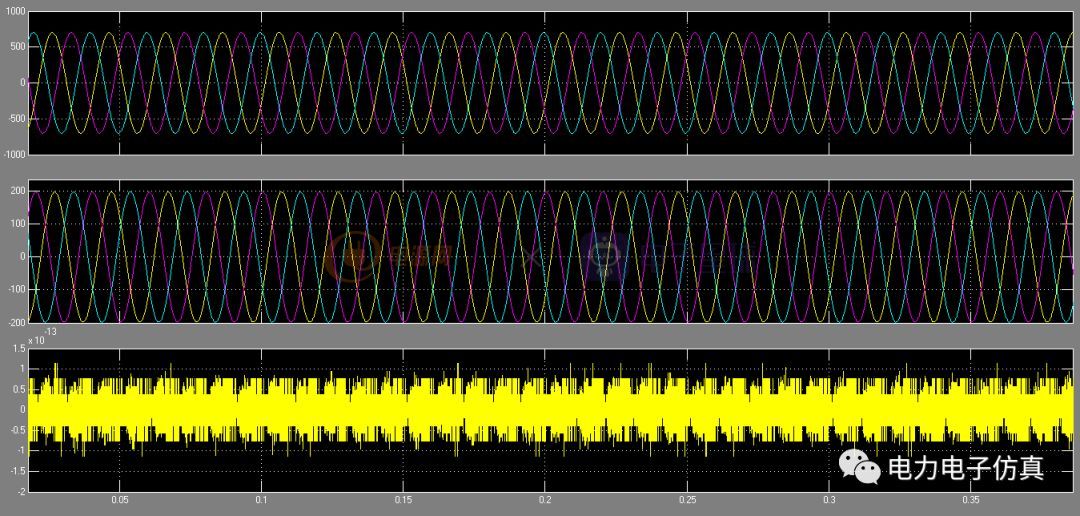
上图分别为正序、负序和零序的电流,从仿真结果颜色可以看出,第一个仿真结果为正序(顺序为蓝黄粉),第二个仿真结果为负序(蓝粉黄),由于负载为角接,故零序为0,即第三个仿真结果。
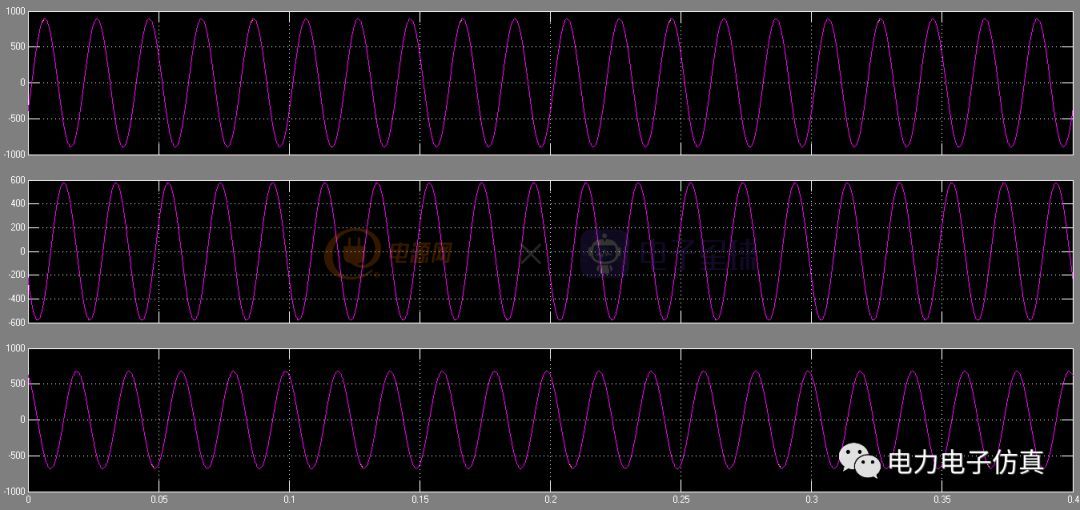
为了验证分离后的电流正确性,分别将abc三相的正序和负序求和,与原电流进行叠加比较,上图为ABC三相原电流和正负序电流求和的叠加波形,从仿真结过可以看出,求和值和原电流完全吻合,证明分离后的正序、负序和零序结果正确。


