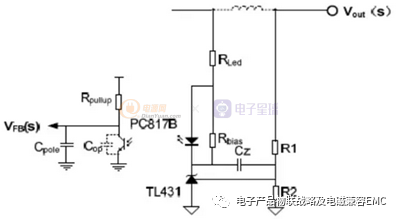
基本的反激变换器原理图如下所示,在需要对输入输出进行电气隔离的低功率<75W~的开关电源应用场合,反激变换器(Flyback Converter)是最常用的一种拓扑结构(Topology)。简单、可靠、低成本、易于实现是反激变换器突出的优点。接下来我将电源的反馈控制环路部分的设计进行说明!

系统反馈环路的计算结果如下:

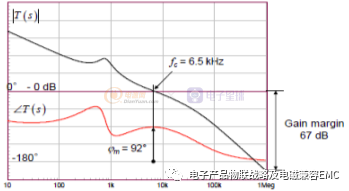
系统的闭环增益及相位请参考如下红色曲线:

增益曲线
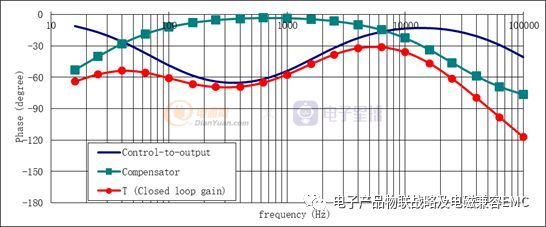
相位曲线
补偿电路设计基本理论分析
开关电源系统是典型的闭环控制系统,设计时,补偿电路的实践与理论相当抽象需要建立模型。目前流行的反激IC控制器,绝大多数采用峰值电流控制控制模式。峰值电流模式反激的功率级小信号可以简化为一阶系统,所以它的补偿电路容易设计。
通常,使用Dean Venable提出的Type II 补偿电路就足够了。
Type II Compensation Circuits:
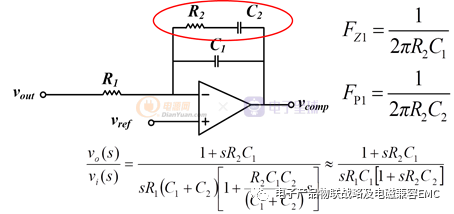


运用如下参数参考设计,通过上面方法;得出增益和相位曲线分析:

如下图示:
Ø Band width:30kHz
Ø Phase Margin:
-155+180 = 25 degree


反激变换器的反馈回路图示
在设计补偿电路之前,首先需要考察补偿对象(功率级)的小信号特性。
如上图所示,从IC 内部比较器的反相端断开,则从控制到输出的传递函数(即控制对象的传递函数)为:
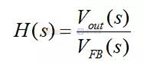
我再将电源的反馈回路进行等效电路分析:
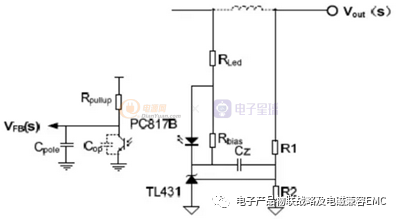


TR :为光耦的电流传输比
Rpullup: 为光耦次级侧上拉电阻
Cop : 为光耦的寄生电容
实际设计中,建议L1 (输出电感)不超过4.7μH。
上述的G(s)函数为标准函数
对CCM 模式反激,其控制到输出的传函为:

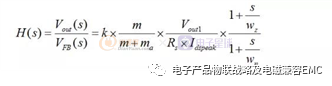
峰值电流模式的电流内环,本质上是一种数据采集系统,功率级传函由两部分Hp(s)和Hh(s)串联组成,其中

Hh(s)为电流环电流采样形成的二阶采样环节(由RayRidley 提出):

其中:

上式中,PO 为输出总功率,k 为误差放大器输出信号到电流比较器输入的衰减系数,Vout1 为反馈主路输出电压,Rs 为初级侧检流电阻,D 为变换器的占空比,n 为初级线圈NP与主路反馈线圈Ns1 的匝比,m 为初级电流上升斜率,ma为斜坡补偿的补偿斜率,Esr 为输出电容的等效串联电阻,Cout是输出电容之和。
注意:CCM 模式反激变换器,从控制到输出的传函,由如下公式 :

可知,有一个右半平面零点,它在提升幅值的同时,带来了90°的相位衰减,这个零点不是我们想要的,设计时应保证带宽频率不超过右半平面零点频率的1/3;由如下公式:

可知,如果不加斜坡补偿(ma=0),当占空比超过50%时,电流环震荡,表现为驱动大小波,即次谐波震荡。因此,设计CCM 模式反激变换器时,需加斜坡补偿。
对DCM 模式反激,控制到输出的传函为:

其中:

Vout1为主路输出直流电压,k 为误差放大器输出信号到电流比较器输入的衰减系数,m为初级电流上升斜率,ma 为斜坡补偿的补偿斜率,Idspeak 为给定条件下初级峰值电流。
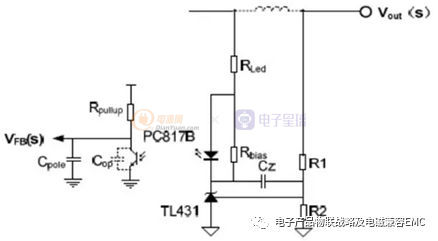


CTR :为光耦的电流传输比
Rpullup: 为光耦次级侧上拉电阻
Cop : 为光耦的寄生电容
实际设计中,建议L1 (输出电感)不超过4.7μH。
上述的G(s)函数为标准函数
通常,为降低输出纹波噪声,输出端会加一个小型的LC 滤波器,如上图
所示,L、C 构成的二阶低通滤波器会影响到环路的稳定性,L、C 的引入,使变换器的环路分析变得复杂,不但影响功率级传函特性,还会影响补偿网络的传函特性。然而,建模分析后可知:如果L、C 的转折频率大于带宽fcross 的5 倍以上,那么其对环路的影响可以忽略不计,实际设计中,建议L不超4.7μH。
于是我们简化分析时,直接将L1直接短路即可,推导该补偿网络的传递函数G(s)为:

其中:

CTR为光耦的电流传输比,Rpullup 为光耦次级侧上拉电阻(对应控制IC,Rpullup=IC的内部电阻)如下图所示:

Cop为光耦的寄生电容,与Rpullup=IC内部的Bias 的大小有关。下图(来源于PC817 的数据手册)是光耦的频率响应特性,可以看出,当RL(即Rpullup)为内部参数时,将会带来一个约10.53KHz左右的极点,所以Rpullup=内部R-Bias的大小会直接影响到变换器的带宽。
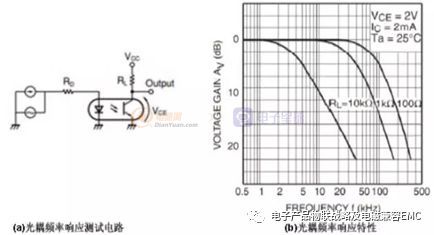
光耦的频率响应
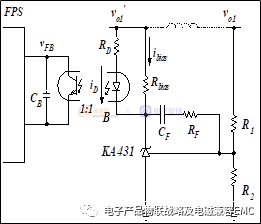
如下计算:

R1与CF 形成了在原点当中的极点,被用来对低频增益进行提升,来压制低频(100Hz)纹波和提高输出调整率,即静态误差。RF&CF 形成一个零点,来提升相位,要放在带宽频率的前面来增加相位裕度,具体位置要看其余功率部分再设计带宽处的相位是多少,RFCF 的频率越低,其提升的相位越高,当然最大只有90 度,但其频率很低时低频增益也会减低,一般放在带宽的1/5 处,约提升相位78 度。
(1) 相位裕度是指:增益降到0dB时所对应的相位。
(2) 增益裕度是指:相位为0deg时所对应的增益大小(实际是衰减)。
(3) 穿越频率是指:增益为0dB时所对应的频率值。
穿越频率,又称为频带宽度,频带宽度的大小可以反映控制环路响应的快慢。
一般认为带宽越宽,其对负载动态响应的抑制能力就越好,恢复时间也就越快,系统从而可以更稳定;缺点是宽的带宽也会带来更多噪声的问题。同时是由于受到右半平面零点的影响,以及原材料、运放的带宽不可能无穷大等综合因素的限制;需要合理化设计!
k Factor(k 因子法)确定补偿网络参数:
★k Factor(k 因子法)是DeanVenable 在20 世纪80 年代提出来的,提供了一种确定补偿网络参数的方法。
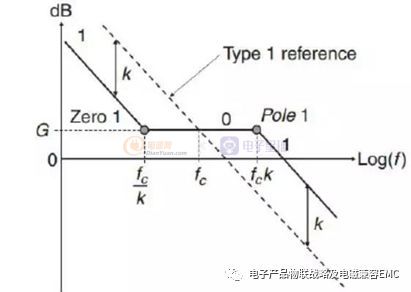
采用K因子确定零点和极点的位置

如上图K因子及补偿参数图所示,将Type II 补偿网络的极点wp 放到fcross的k 倍处,将零点wz 放到fcross的1/k 处。上面的补偿反馈的补偿网络有三个参数需要计算:RLed,Cz,Cpole,下面将用k Factor 计算这些参数:

动态负载时输出电压波形
由此通过上面的假设参数进行理论数据推导如下:
-----确定补偿后的环路带宽fcross:通过限制动态负载时(△Iout)的输出电压过冲量(或下冲量)△Vout,由下式决定环路带宽:

--考察功率级的传函特性,确定补偿网络的中频带增益(Mid-band Gain):
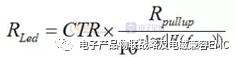
--确定Dean Venable 因子k:
选择补偿后的相位裕量PM(一般取35°~80°),由如下公式

得到fcross 处功率级的相移(可由Mathcad 计算)PS,则补偿网络需要提升的相位Boost 为:

推荐PM=70 PS=-100
则k 由下式决定:

--补偿网络极点(wp)放置于fcross 的k 倍处,可由下式计算出Cpole:

--补偿网络零点(wz)放置于fcross 的1/k 倍处,可由下式计算出Cz:

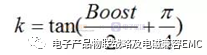

通过设计经验推荐K=3--4; PM=70 PS=-100进行取值K=3.24
因此如下原理图参数均可全部设计确定下来:
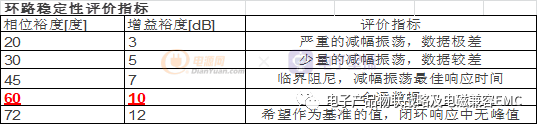
总结:一般可从以下三个原则判定电源环路稳定性:
(1)、在室温和标准输入、正常负载条件下,闭环回路增益为0dB(无增益)的情况下,相位裕度是应大于45 度;
如果输入电压、负载、温度变化范围非常大, 相位裕度不应小于30度。
(2)、同步检查在相位接近于0deg时,闭环回路增益裕度应大于7dB,为了不接近不稳定点,一般认为增益裕度12dB以上是必要的。
(3)、同时依据测试的波特图对电源特性进行分析,穿越频率按20dB/Dec闭合,频带宽度一般为开关频率的1/20~1/6。
零极点频率引起的增益斜率变化规则




开关电源系统瞬态负载条件下的几种典型响应波形可供 设计参考!
通过上面的理论和实践的运用,我们的设计参数一般会按IC-DS推荐的参数进行设计;其设计结果不会有太大的问题;但对于我们想了解我们参数的最佳值我还是推荐仪器测试法来实际测量-让系统有最佳的系统稳定性设计。

电源环路及系统的稳定性评估分析工具(强烈推荐)
运用我制作的测试工具板来验证系统环路的稳定性方法;我通过MOS的开关来增加系统的输出电流;来测试瞬态输出变化电流和输出电压的变化情况;来分析系统在不同负载条件下的环路的稳定性
(让系统有最佳的增益和相位裕度设计!)

CH-绿色:输出电流的波形 CH-蓝色输出电压波形
说明:
MOS的响应时间500nS 固定负载初值:为负载的10%
可以再外加10%-100% 动态MOS控制负载为>10%
MOSON的时间为 5%的Duty 导通时间(防止MOS串联的电阻长时间发热)

该稳定性评估分析工具:由MCU驱动高速MOS组成,MOS的响应时间<500nS
说明:用MCU 来做PWM驱动,5%Duty mos开通时间,6V驱动(电池供电)频率可选!便于随身携带;不需要外部的交流电源系统!@!
注意:MOS-ON的时间=5% * T
F-drv=100HZ T=10mS MOS-Ton=0.5ms=500us
F-drv=200HZ T=5mS MOS-Ton=0.25ms=250us
F-drv=300HZ T=3.3mS MOS-Ton=0.167ms=167us
F-drv=500HZ T=2mS MOS-Ton=0.1ms=100us
F-drv=1KHZ T=1mS MOS-Ton=0.05ms=50us
这个评估板的设计,MOS/F-Drv频率由拨码开关组合选择,MOS/ON的时间也可以由拨码开关组合选择;适合所有拓扑结构方案的环路设计评估!
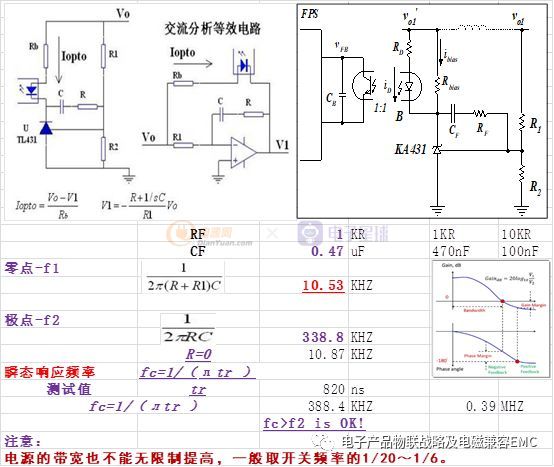
测试非常好的波形分析评估如下:(优化反馈系统参数及光耦参数即可)
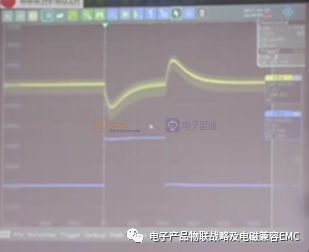
瞬态的响应频率F=1/(лTr)=0.3/Tr
测试图中的瞬态时间(高点到低点的时间)=23uS
F=1/(лTr)=0.3/Tr=0.3/23us=13KHZ
电源的补偿(COMP)计算零点时的频率
f=1/(2ЛR*C)
f < F的频率 系统就OK啦;实际测试如下图的理论计算数据相一致!



