电源工程师对于开关电源峰值电流型控制都比较熟悉,由于峰值电流型小信号精确模型的传递函数比较复杂,所以对于环路稳定性的设计一般都采用仿真的方法。笔者试图通过建模,用解析的方法来分析环路的稳定性,然后阐述电流内环参数的选择对电压外环的影响。
对于开关电源峰值电流型反馈控制系统的精确建模,张卫平教授在他的著作《开关变换器的建模与控制》一书中,已经给出了完整的推导过程,这里笔者就不再赘述了,感兴趣的读者可以自行查看该书(新版)的第6章节的内容(从186页到226页)。该书推导了从控制电压Vc(s)到占空比d(s)的这一环节的传递函数,但没有进一步论述外部的电压环路传递函数和斜率补偿对电压环路稳定性的影响。笔者就在张卫平教授推导模型的基础上,再推导完整的峰值电流型传递函数。接下来以BUCK电路为例说明,下图为张教授推导的峰值电流型控制的小信号模型(时域下)。
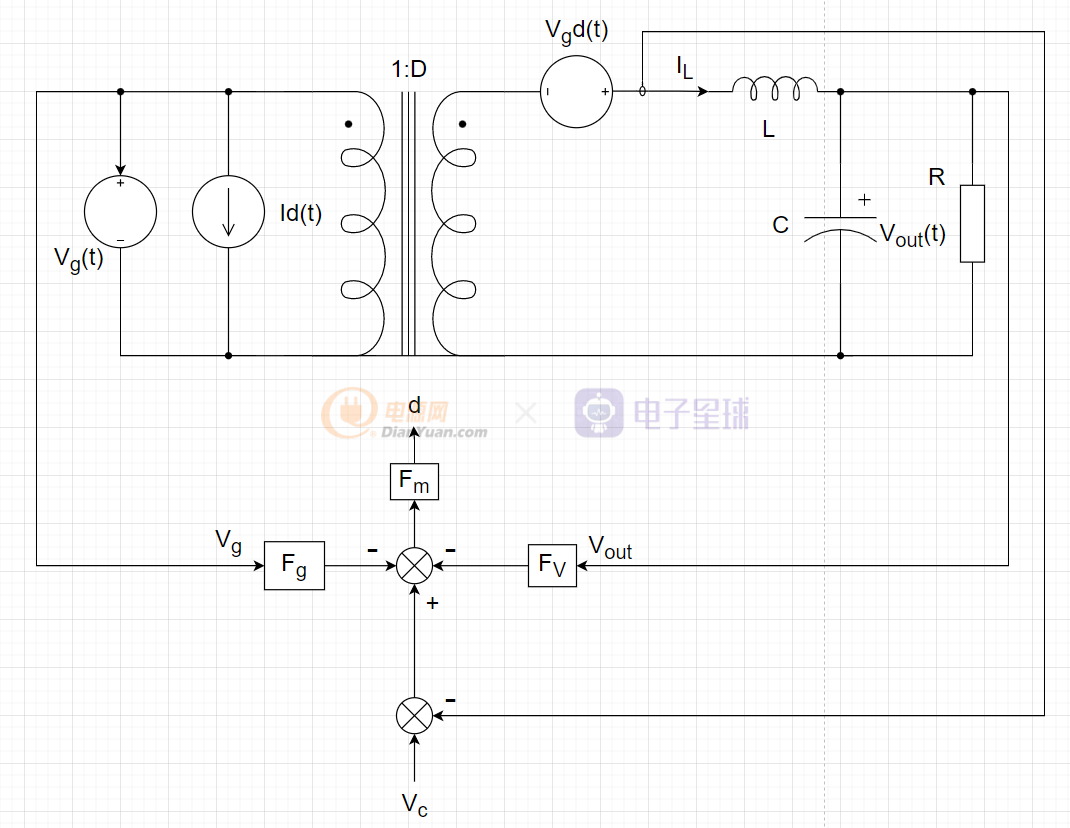
其中,
,
D为占空比直流量,d(t)为占空比小信号扰动,Ts为PWM的开关周期,L为电感量,Ma为斜率补偿系数。
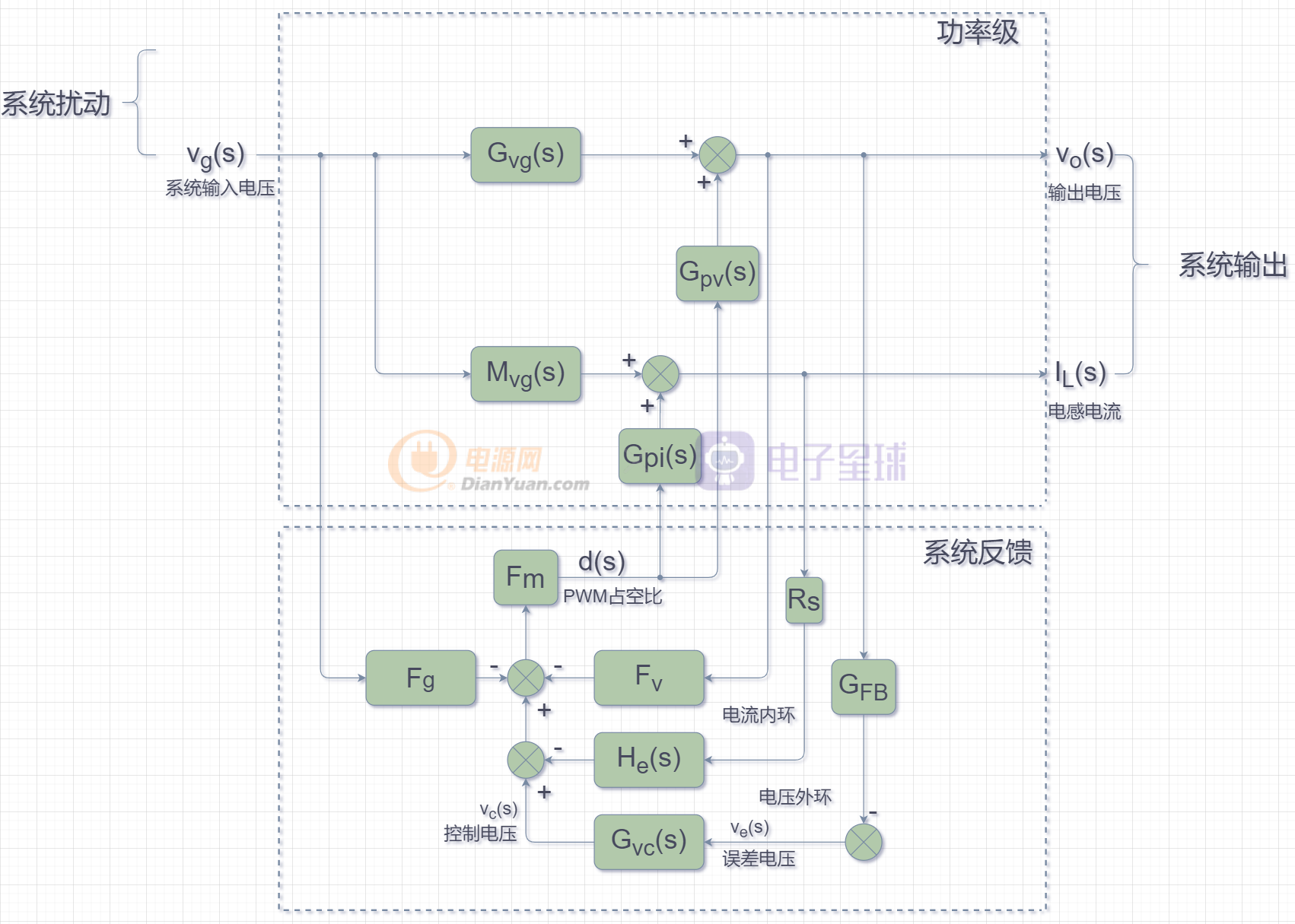
以上面的模型为基础,再添加上输出电压及电感电流的反馈、占空比d(s)对输出电压和电感电流的控制,从而得出通用开关电源电路的拉氏变换控制系统框图如下:

上图中有两点需要说明一下:
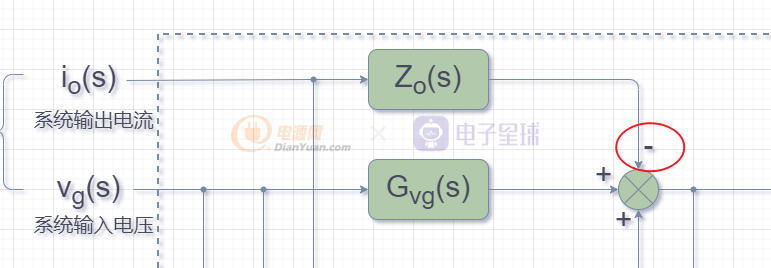
因为输出电流io(s)的增加,会引起输出电压Vo(s)的下降(电源输出阻抗),所以上图中的红圈为负。
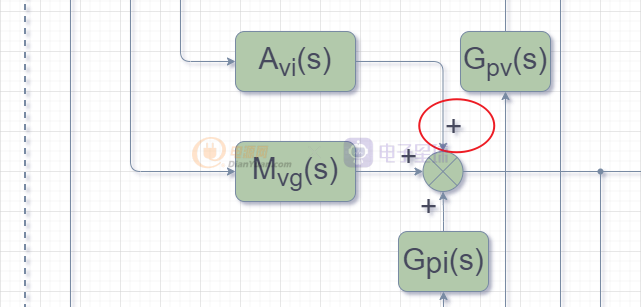
因为输出电流io(s)的增加,会引起电感电流IL(s)的增加,所以上图中的红圈为正。
在功率级框图中,系统的输入电压和输出电流做为系统的扰动,输出电压和电感电流做为系统的输出,输出电压设定(Vref)做为控制系统的输入,d(s)占空比分别控制输出电压和电感电流。上图中的绿色方框部分有的已经建模得到了相关的传递函数,剩下没有建模环节的传递函数将通过下面的推导得出。
通过对开关量进行小信号线性等效,并将元器件中的寄生参数考虑进去(Re为电感的等效电阻,Rc为电容的等效串联电阻,RL为负载电阻),可以得到如下的BUCK变换器的模型(s域):
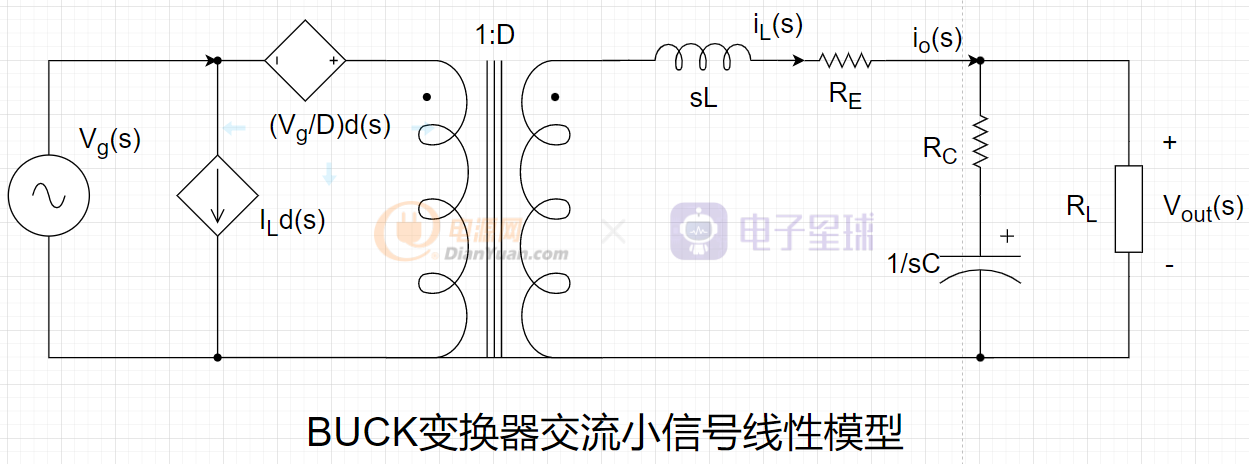
Vg表示直流量,Vg(s)表示小信号交流量。同理D表示直流量,d(s)表示小信号交流量,电路中其它变量交直流量表示方法也相同。
1)求Gvg传递函数
表示Vg(s)单独影响Vo(s),所以要将d(s)置零并将io(s)对Vo(s)的影响忽略,从而得到下面的框图:
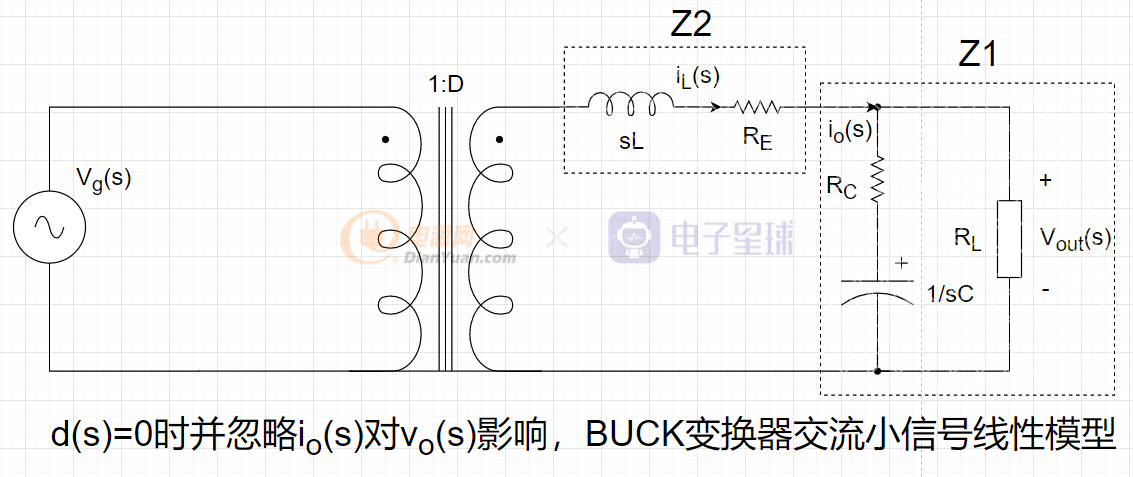
通过上图可得:
化简可得:
2)求Mvg传递函数
根据上图中次级回路的结构,可得到方程:
化简可得:
3)求Gpv传递函数
,所以要将vg(s)置零并将io(s)对Vo(s)的影响忽略,可以得到如下的框图:
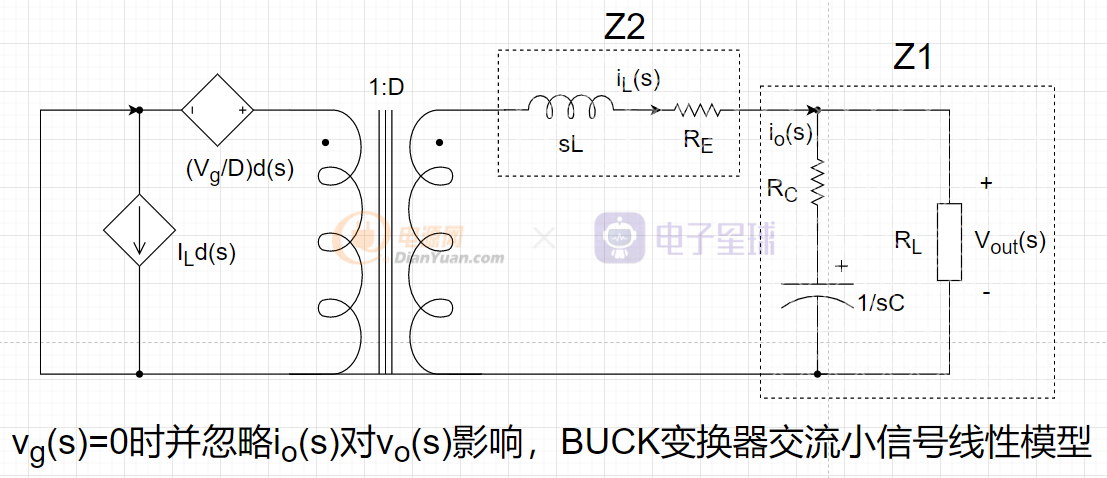
化简可得:
4)求Gpi传递函数
同样根据上图,有如下方程:
化简可得:
5)求Zo(输出阻抗)传递函数
将vg(s)和d(s)置零,得到如下框图:
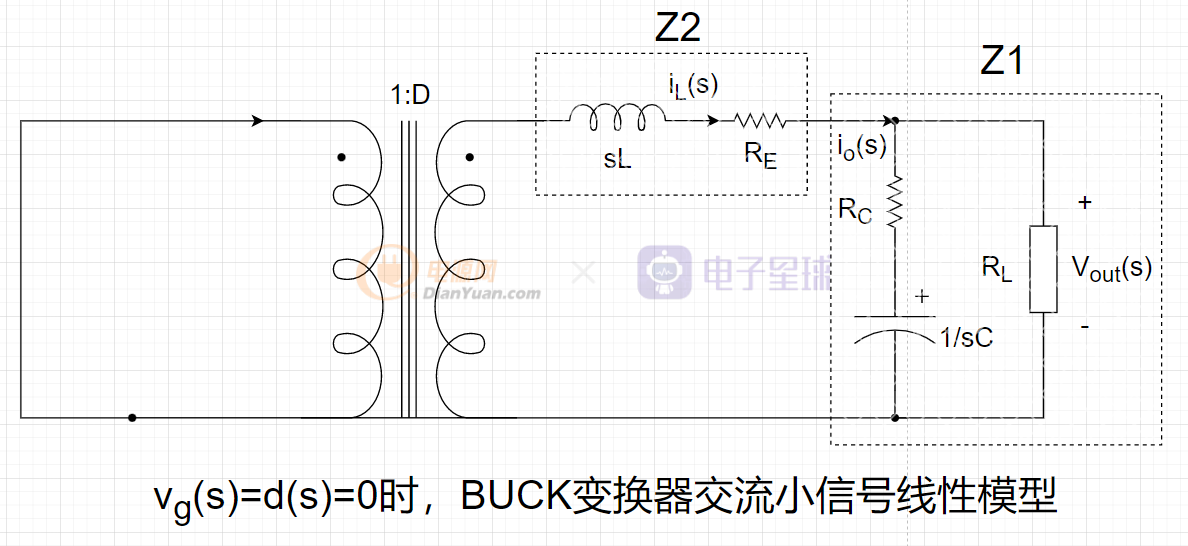
有如下的方程:
化简:
6)求Avi传递函数
化简:
至此,已经将功率级环节所有的传递函数推导出来。
另外,电感电流采样环节分为两部分:Rs(电流互感器等效电阻),He(s)(连续域电流峰值采样传递函数)。
其中He(s)可以近似等效为:
式了中的,
接下来,以一个BUCK电路为例,来具体说明是如何应用上面推导出的传递函数计算电压环路的补偿Gvc
BUCK电路的参数如下:
输入电压: 30V最小 60V最大 45V额定值
输出电压:15V
输出电流:10A
开关频率:100KHz
互感器的匝比: 1:100
互感器次级取样电阻:15Ω
电感量:28uH,等效电阻2mΩ
输出电容:330uF,等效电阻20mΩ
一)电流内环的Bode图:
电流内环框图:
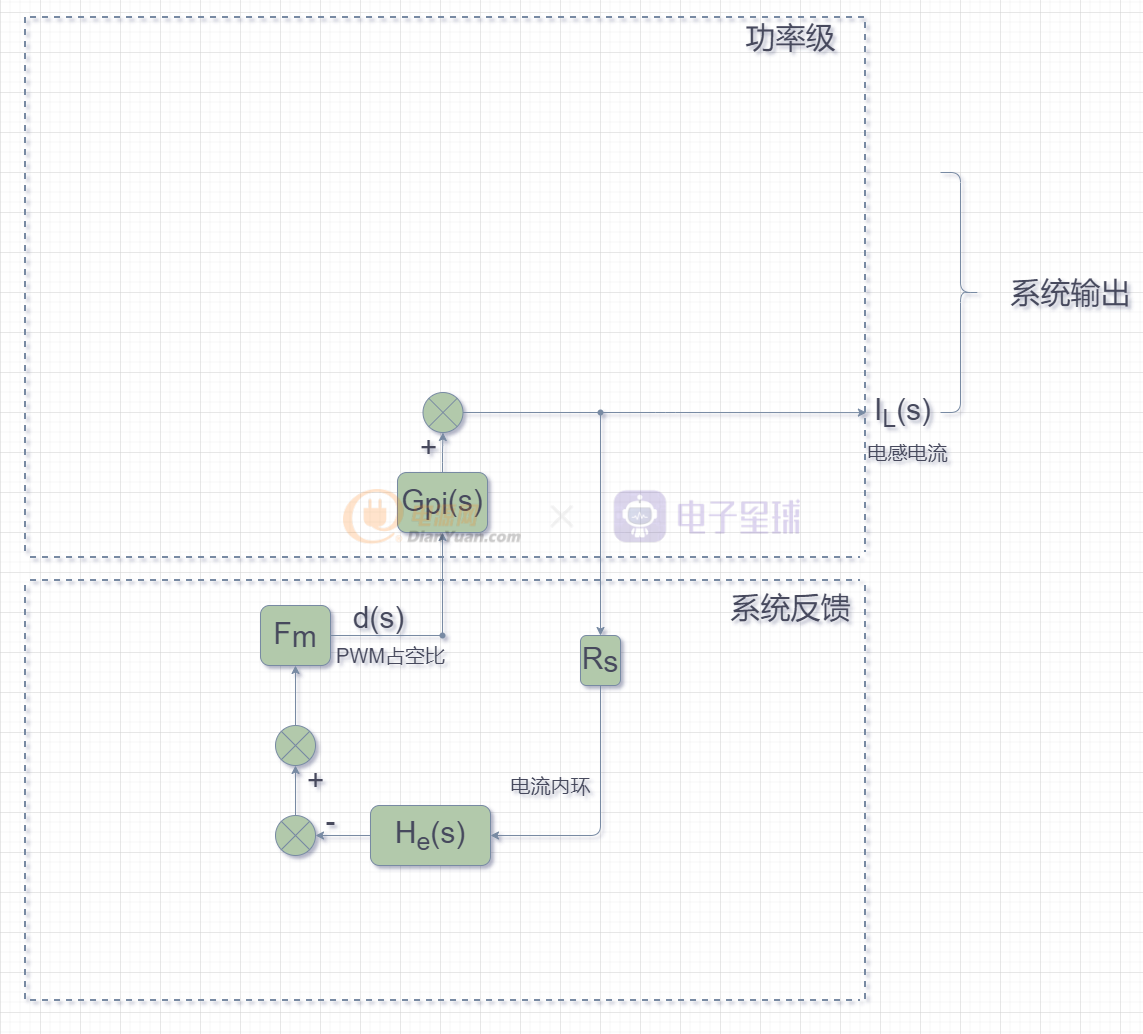
内环电流环路设计的主要目标是:找到斜率补偿系数Ma的值,使电感电流IL(s)稳定,不会产生次谐波振荡。根据上图,可以得到电流环路的开环增益Ti(s):
其中:
用MathCAD绘制Ti(s)的bode图,并以Ma为变量进行扫描,画出曲线:
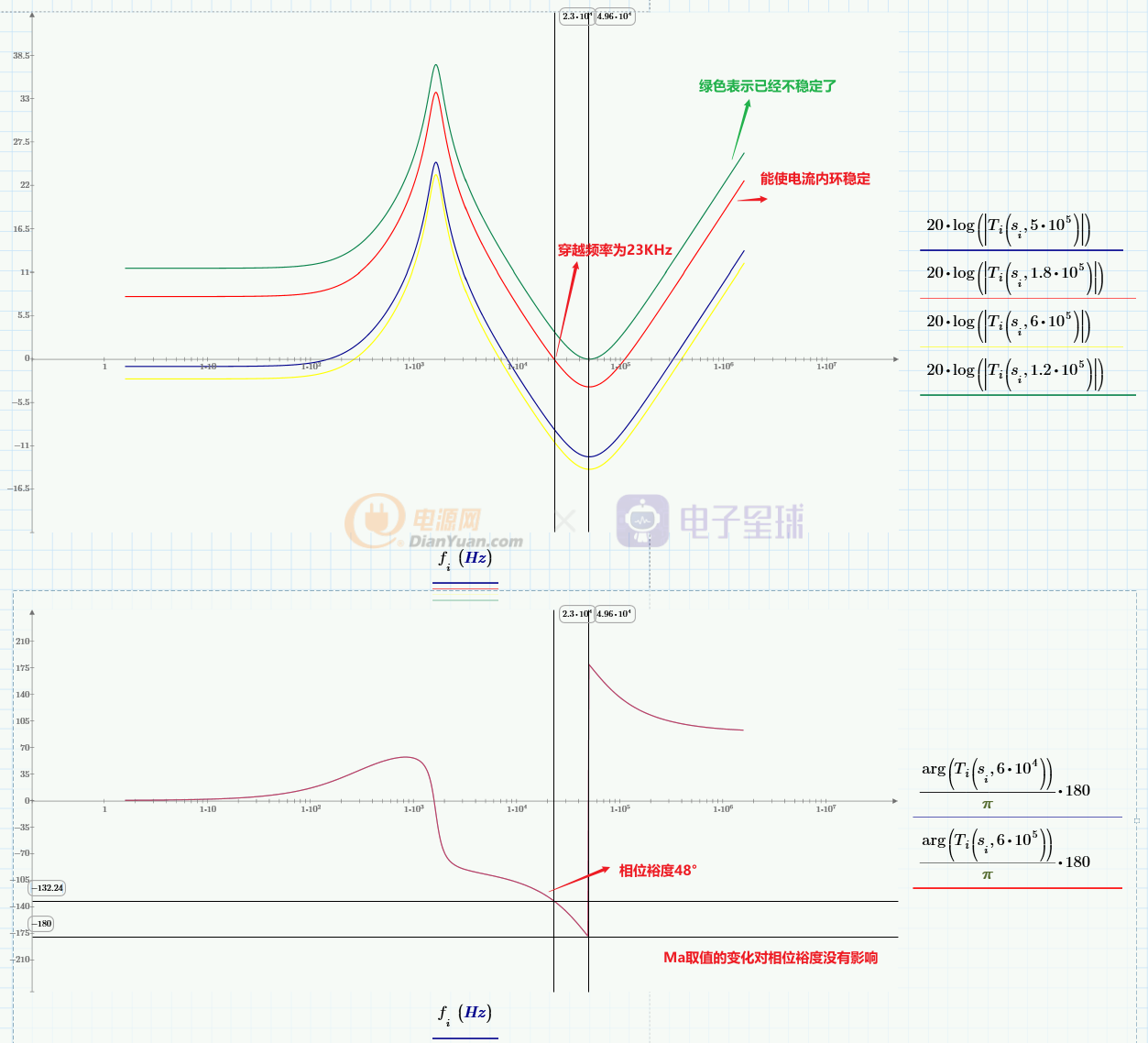
Ma的取值从1.2*10^5 A/s到6*10^5 A/s,可以得到一组曲线,当Ma小于1.2*10^5 A/sec,环路就不再稳定。Ma也不是越大越好,Ma的增大会降低穿越频率,导致电流内环的响应变慢,还会影响抗输入扰动的性能和输出的阻抗。
二)控制电压Vc(s)到输出电压Vo(s)的传递函数Ac(s):
将Vg(s)和Io(s)置零后,可以得到如下的框图:

根据上面的框图可以得到两个等式:
从而可得:
画出bode图:


当Ma小于等于1.2*10^5以后,将会出现不稳定的状态。随着Ma的增大,会发现Ac(s)逐渐向电压型控制状态演化,当Ma取值6*10^6时,已经完全演变为电压型控制。
在本环节,Ma的取值原则是:削掉幅频曲线中的尖峰,同时要保证不会变为电压型控制环路。Ma既不能太小,也不能太大。这与调试中的经验比较吻合,Ma补偿不够时,会出现次谐波振荡,Ma补偿过大,就会变成电压型控制。
三)抗输入扰动Mvcl(s)(电流闭环,电压开环情况下):
在忽略io(s)的影响且Vref置零的情况下,得到如下框图:
根据上面框图,可得到一组方程:
化简:
因为要求得输出电压的变化,所以应当将电压环路断开,电流内环闭合时,画出Mvcl的bode图:
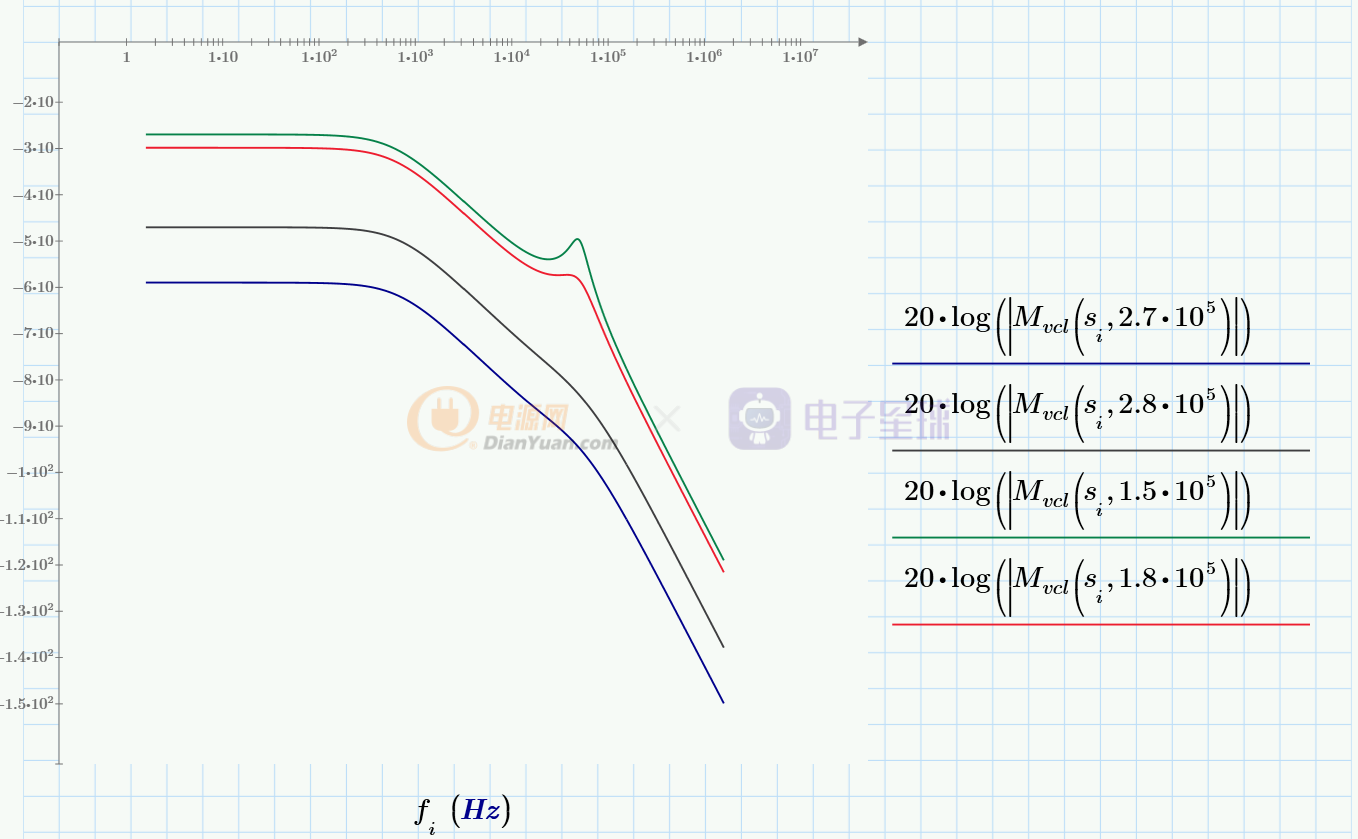
可以看到,Mvcl(s)增益越小(曲线越低),输入电压Vi(s)对输出电压Vo(s)的影响越小。随着Ma的变化Mvcl(s)增益并不单调,当Ma取值2.7*10^5时,Mvcl的增益最低,即输入电压Vi(s)对输出电压Vo(s)的影响最小
四)输出阻抗Zocl(s)(电流闭环,电压开环情况下):
当Vg(s)=Vref=0时,得到如下方框图:
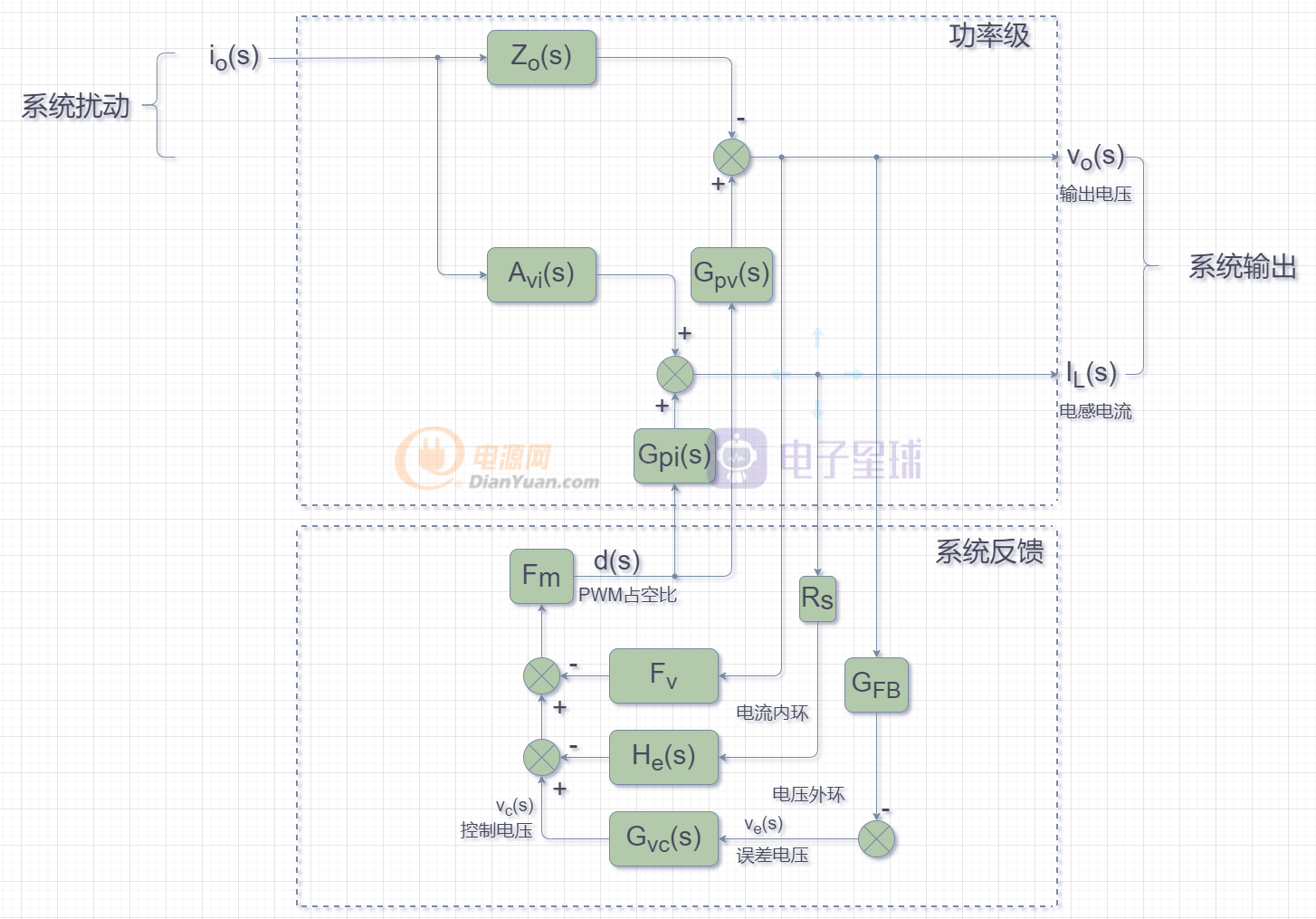
有下面一组方程:
化简:
在电流内环闭合,电压外环开环的情况下,画出bode图:
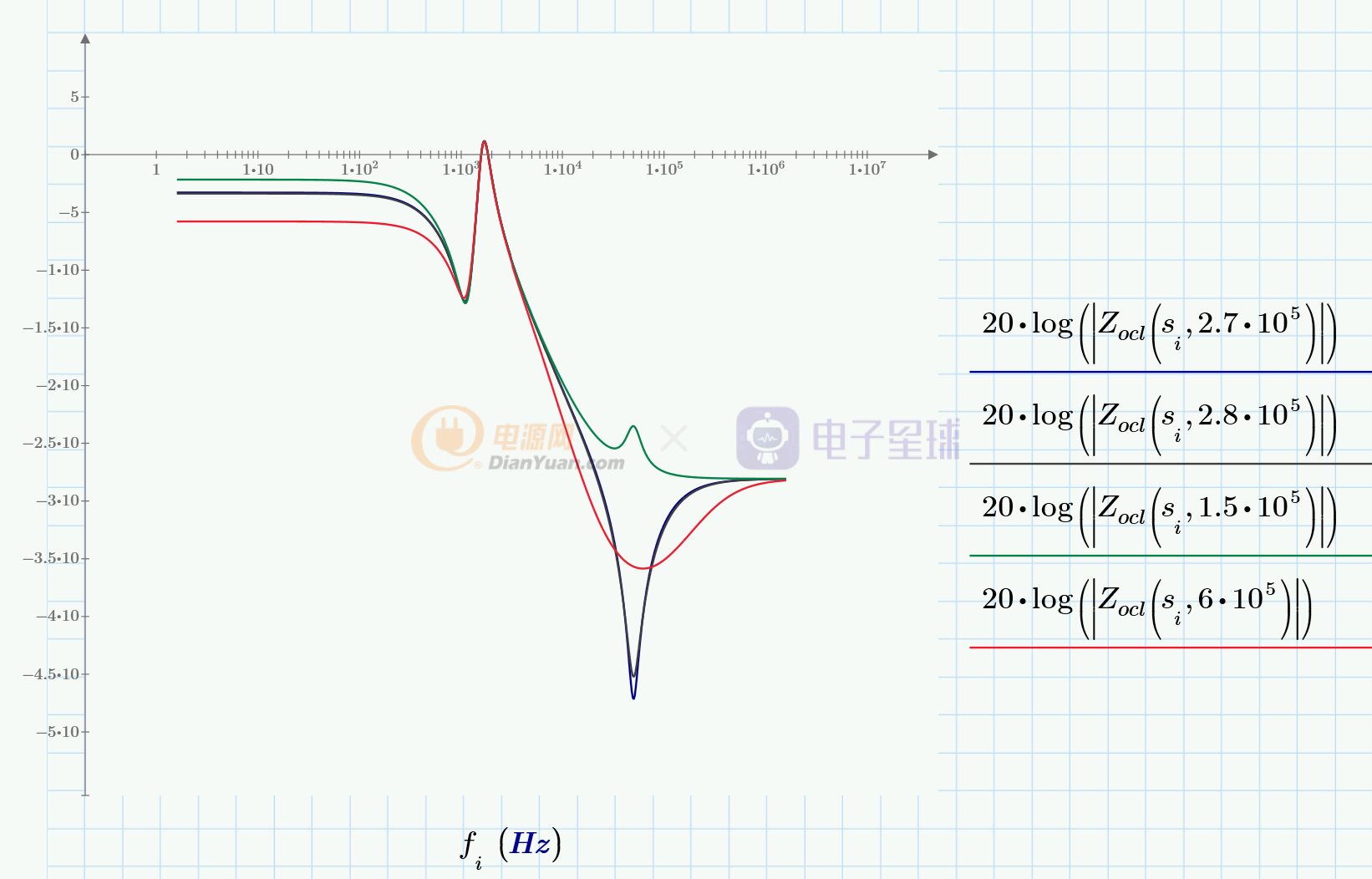
注意Zocl(s)的增益是个负数。在低频段,|Zocl(s)|绝对值越大(曲线越低),对Vo的影响越大。即:在低频段,随着Ma的取值的增大(曲线越低),抵抗负载扰动的能力越差,因此从负载抗扰动的角度看,Ma的取值越小越好。
上面的计算过程,分别从电流环路稳定性、电流型向电压型的演化过程、输入电压抗扰度和负载抗扰度这四个方面说明了斜率补偿系数Ma的选择原则,综上可以选择:
下面就以Ma这个值为基础来计算外部电压环路的补偿参数。
首先,根据Ma的取值,画出电流环路的开环增益Ti(s)的bode图:
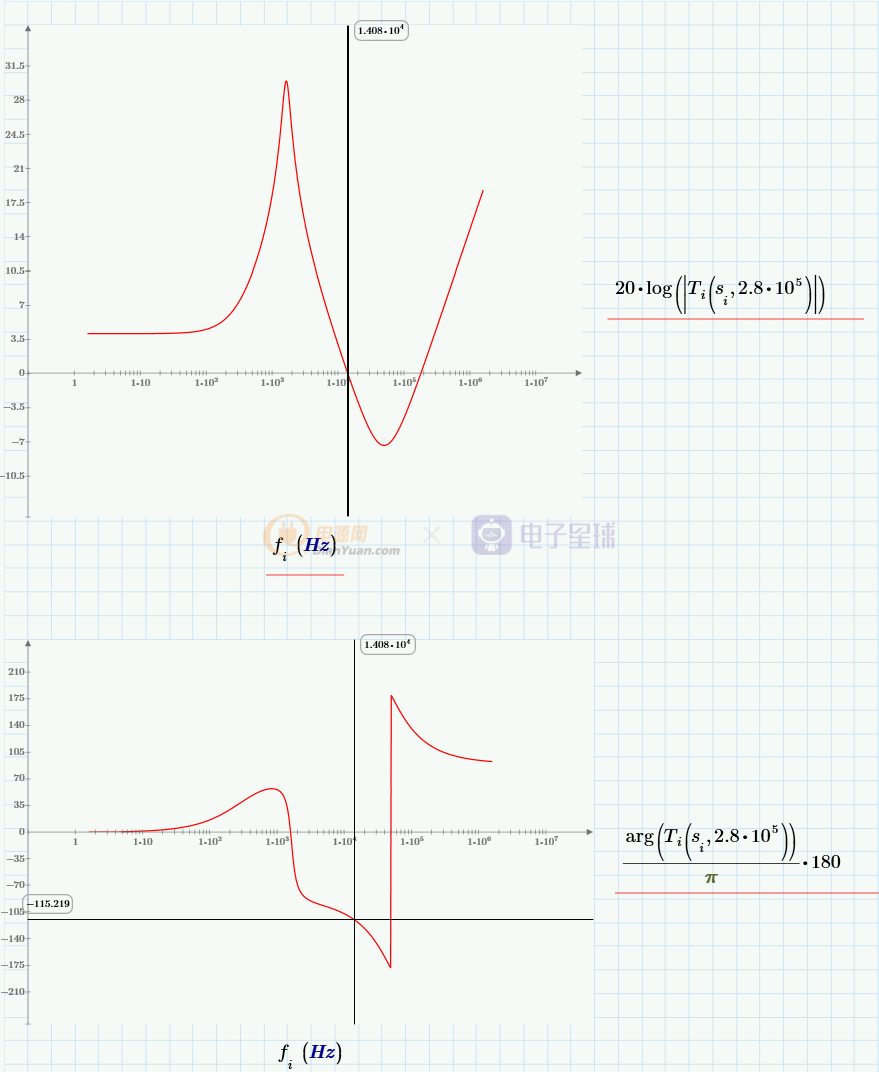
穿越频率14KHz,相位裕度65°。
Vc到Vo的传函Ac(s)的bode图:
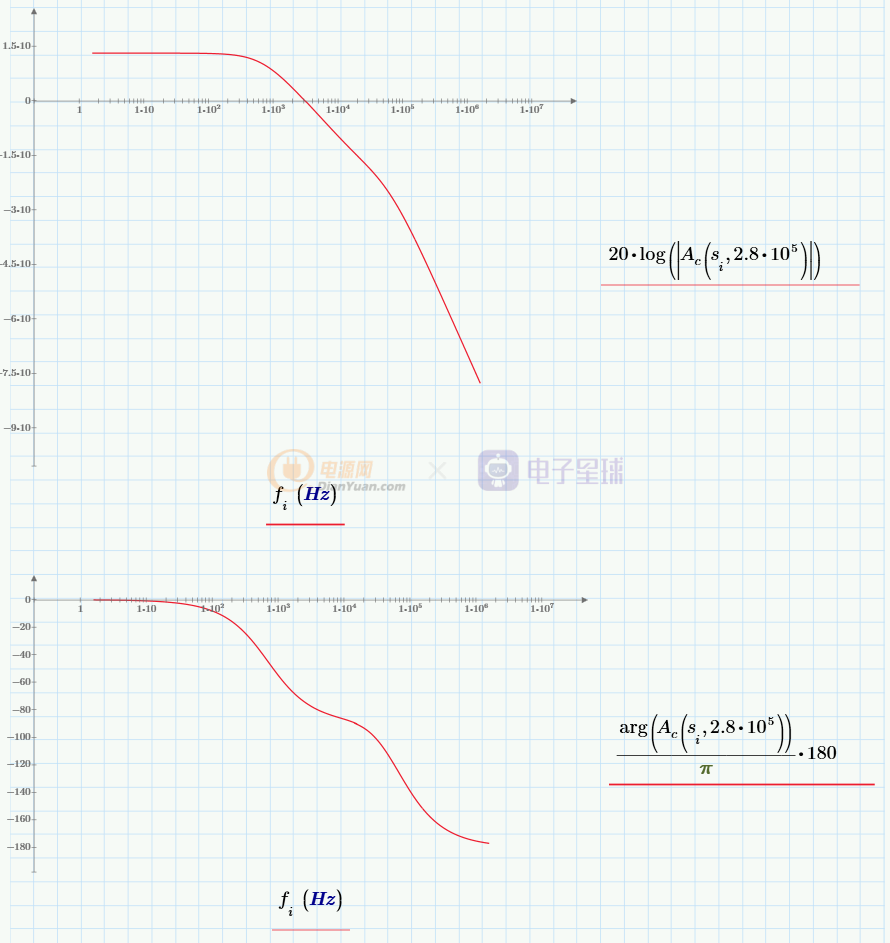
上图中的Ac(s)已经是稳定的状态了,只是低频的增益比较小,稳态误差较大。
五)电压环路设计:
将前面的电压环路进行整理得到框图:
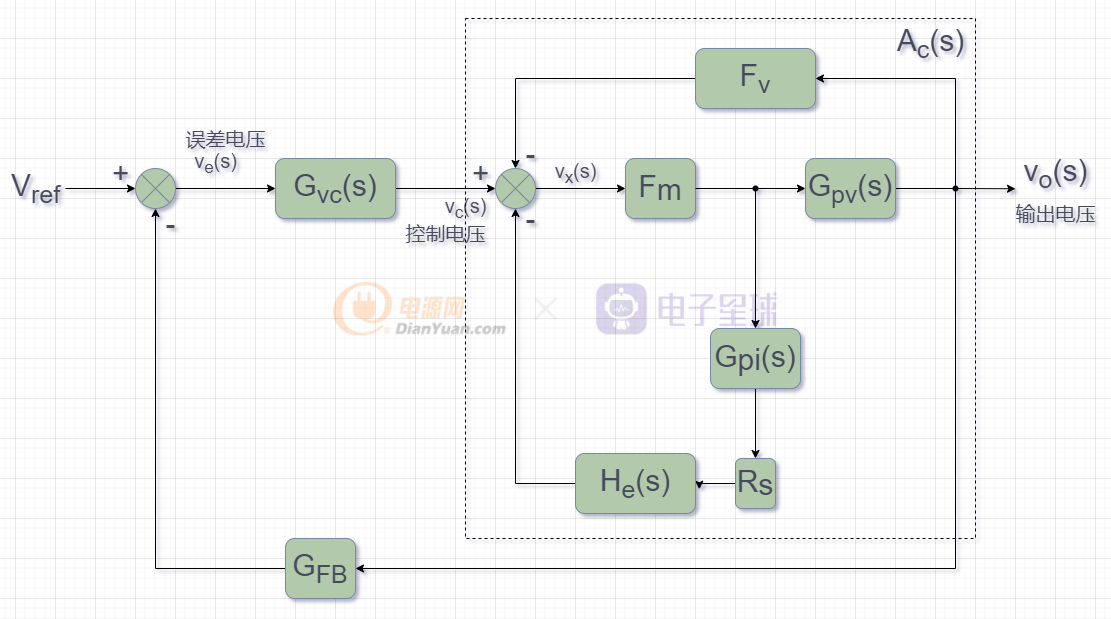
因为控制电压Vc到Vo的传递函数Ac(s)已经在前面求得,所以电压环路开环增益Tv(s)就是:
电压环路的设计,主要是加大电压环路低频开环增益以消稳态误差,并让幅频曲线穿越频率尽量高些,保证快速性,因此针对Gvc(s)补偿的需求,可以用下面的电路:
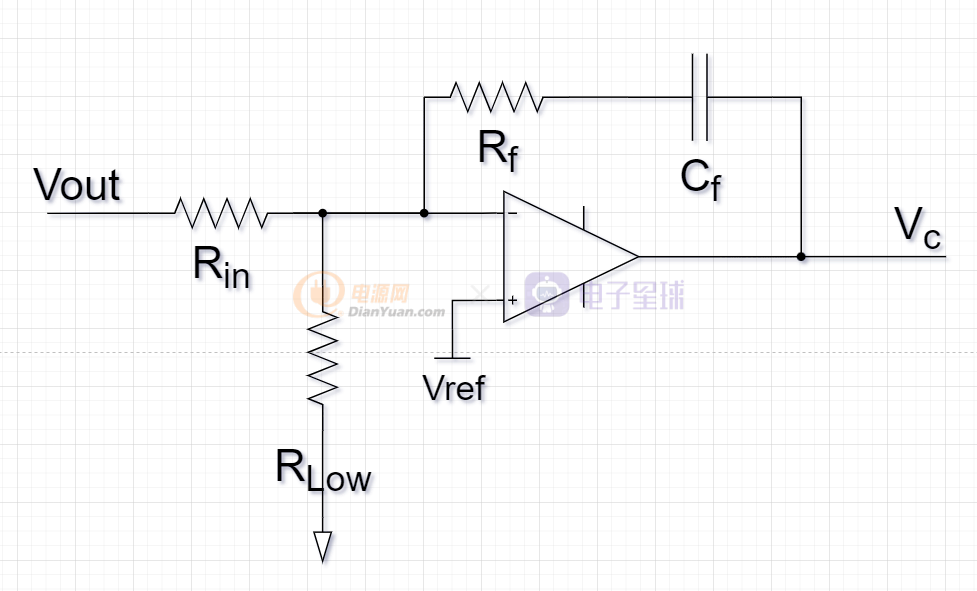
把Gvc(s)传递函数的零点放在600Hz,初始极点1.5KHz位置后,经过计算,得到如下参数:
Rin=10k RLow=2k Cf=10.6nF Rf=25k
根据上面参数,画出Gvc(s)的bode图:

需要注意的一点是:上图中的补偿器的传递函数已经包含GFB及相减的功能了,所以电压环路开环增益Tv(s)改为:
然后,以上组参数为基础,画出Tv(s)的bode图:
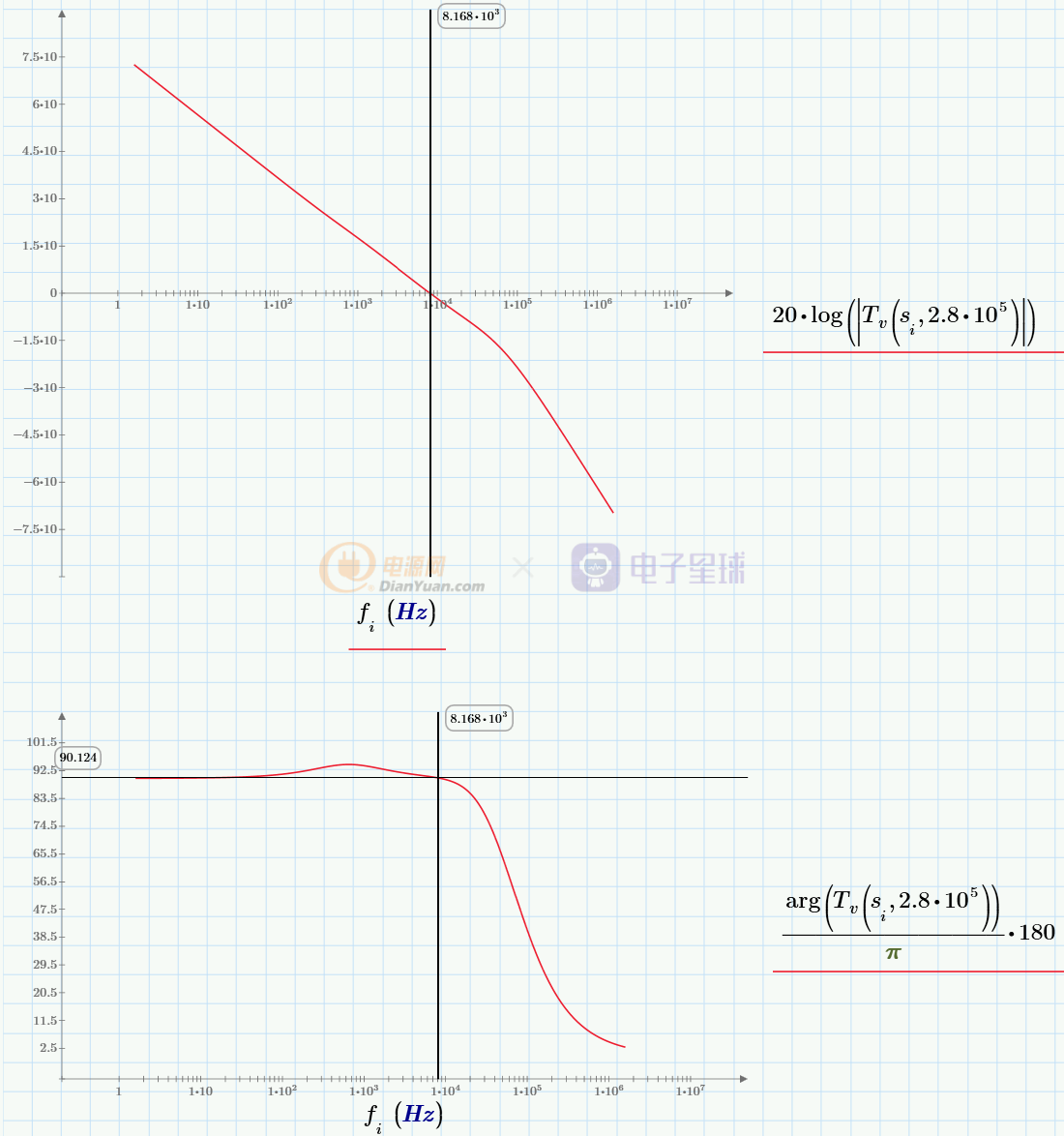
从该图中,可以看到电压开环bode图的穿越频率为8.2KHz,相位裕度为90°。
再用SIMPLIS仿真验证上面的计算是否正确。
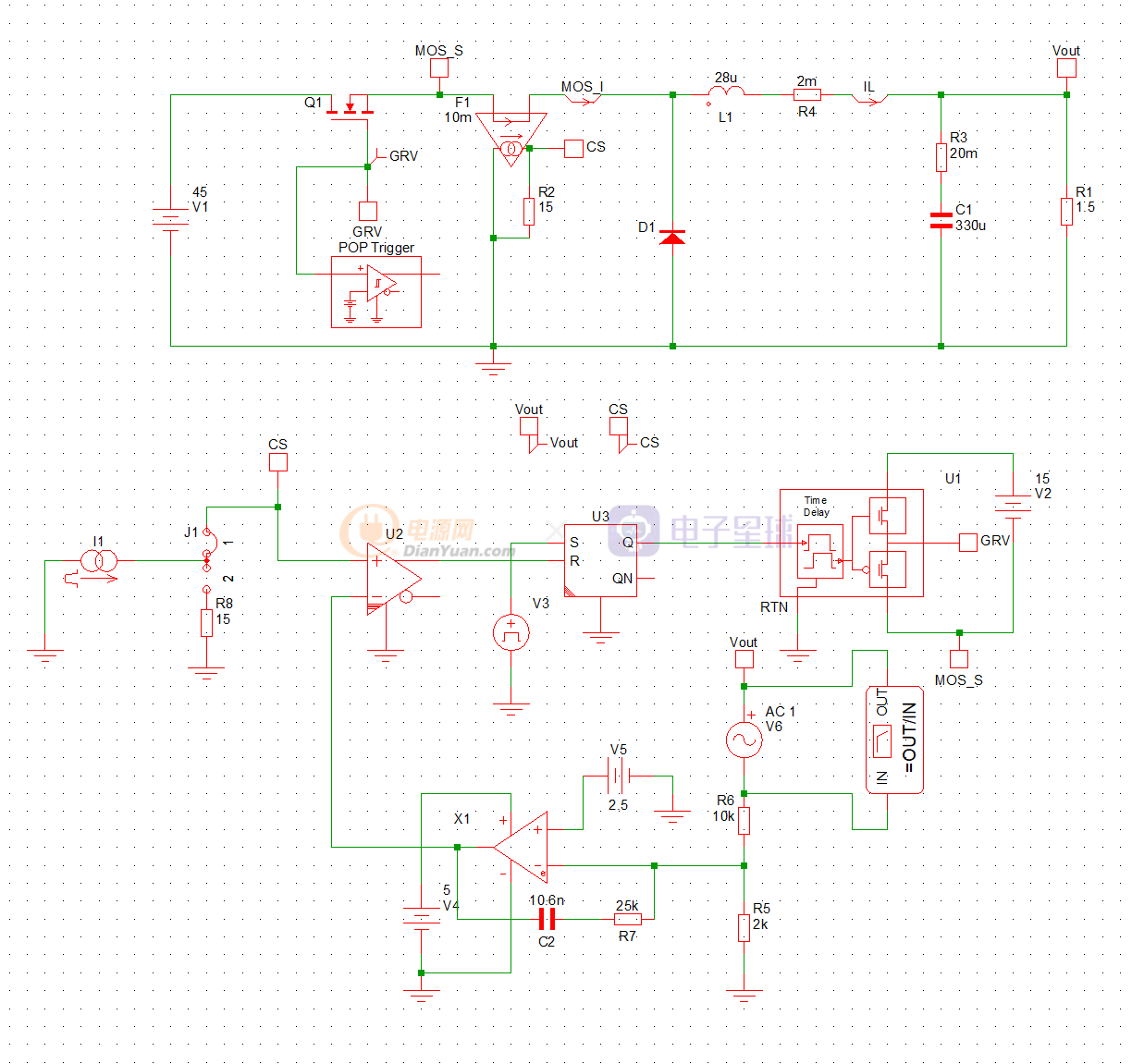
通过AC交流仿真后,得到电压环路的bode图:
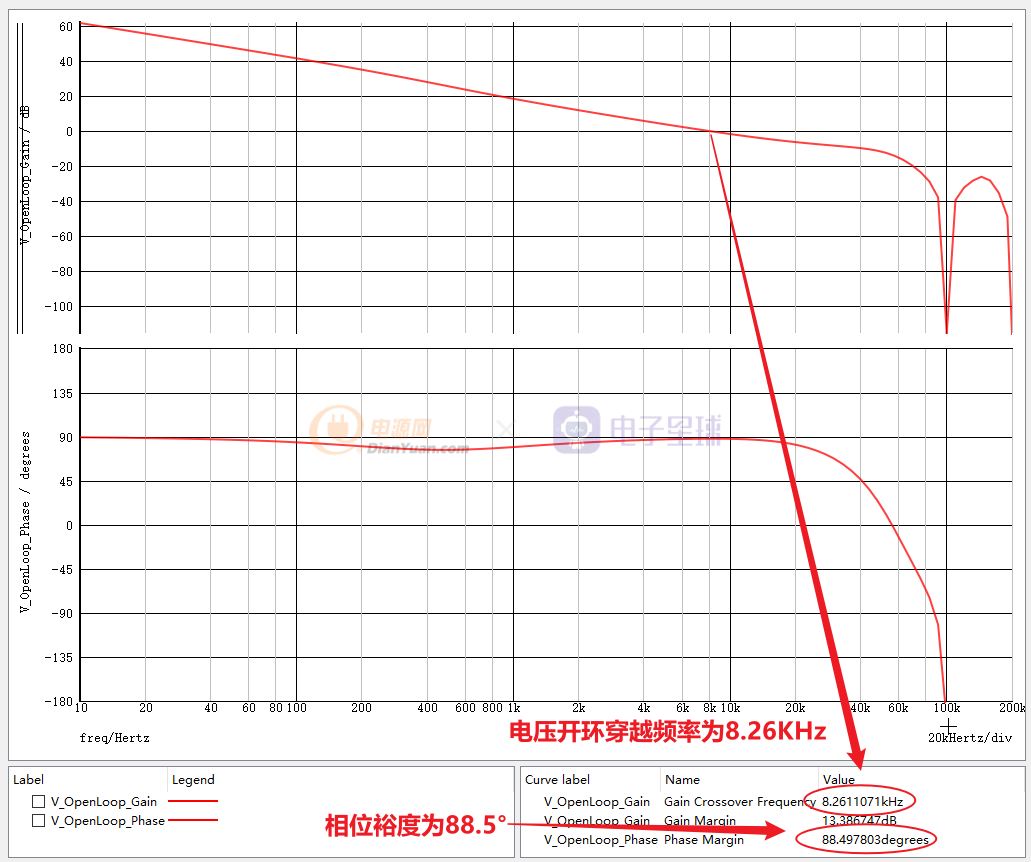
仿真得到电压开环穿越频率为8.26KHz,相位裕度为88.5°,与解析法计算出来的结果相一致。证明了解析法的正确性。
从仿真出来的波形看,该曲线能仿真出开关频率对bode图的影响,而解析法无法计算出来。
最后总结:
峰值电流控制环路计算的起点是Ma的选择,Ma不仅影响电流内环的稳定性,还对输入抗扰性、负载抗扰性及电压环路也有很深的影响,通过解析的方法,可以发现Ma的变化是如何将电流型演变成电压型的。
一般,对于BUCK电路来说,占空比不超过50%时,IL(s)是不存在振荡的,是内在稳定的,理论上不需要斜率补偿。但Ma斜率补偿的选择却会影响电压环路的稳定,所以即使占空比不超过50%,也应该选择合适的Ma,然后再计算电压补偿参数。
在附件中有本例全部的计算书及仿真文件,计算书是用MathCad Prime 8.0编写的,版本低的请自行升级。仿真文件用Simplis 8.40b版本。


