大家好,我是电源漫谈,很高兴和各位一起分享我的第43篇原创文章,喜欢和支持我的工程师,一定记得给我点赞、收藏、分享。
电容是最普遍的三个无源电子元件电阻,电容,电感其中的一员,在各种电子电路中都广泛使用,其性能会影响到电子电路的特性,所以有必要对其主要特性及功能做一全面理解,方便在电路设计中扬长避短。
一.电容的基本直流特性及结构介绍
电容可以反复充电和放电,这一点类似于电池,但是和电池的区别是它存储的能量比较少,所以放电时持续的时间也相对较少。
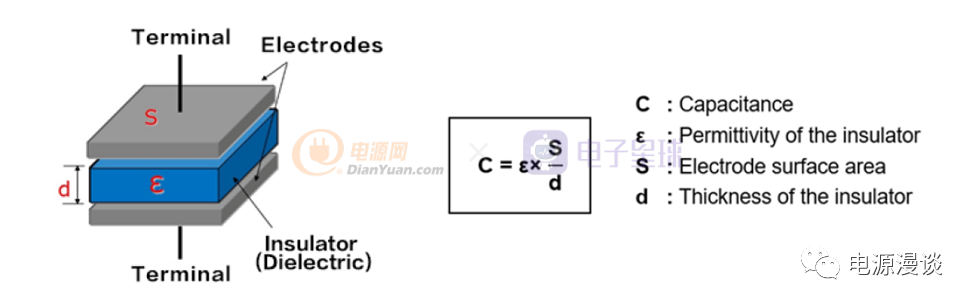
图1 电容的基本结构
电容的基本结构如图1所示,它由两个相对的金属电极板和中间的绝缘层组成,在电极之间施加直流电压,则会在电容上存储电荷,这就是电容储能的基本原理。如图示的结构所见,这个电容的电容量取决于其结构因素,和金属极板面积S成正比,和金属极板之间的绝缘层厚度d成反比,和介电常数成正比。
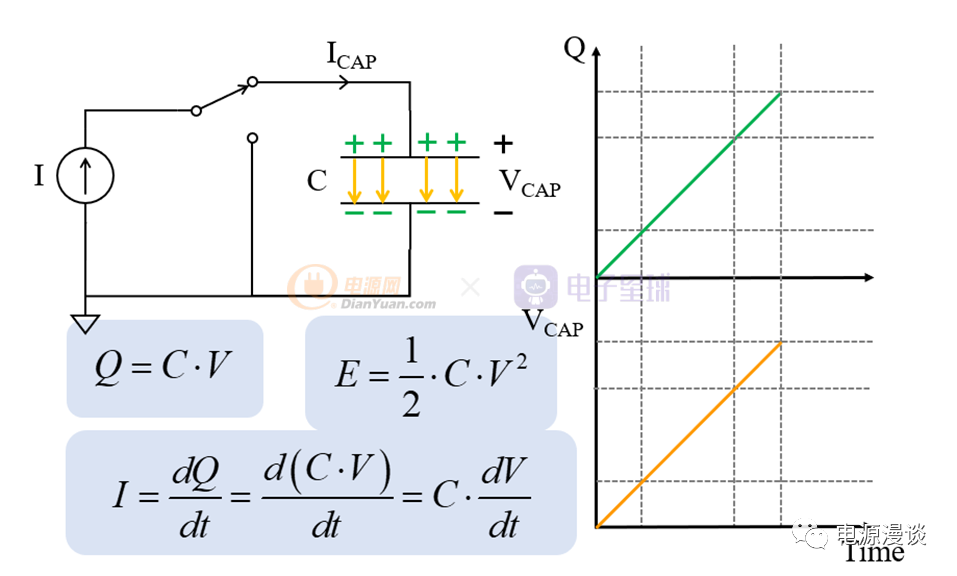
图2 电容恒流充电过程
通过一个恒流源I,给电容进行充电,则我们很容分析出电压的变化率和电流成正比,这个比例系数也就是电容C,从图2上的充电曲线来看,根据电容电荷基本关系,Q=C*U,随着时间的变化,电压以线性上升,电荷存储量也线性上升。通过上述分析,我们可以得知,电容电压的变化率和电容电流成正比。
接下来,我们通过仿真来探讨一下电容的基本充放电特性。电容充电的仿真原理图如图3所示。
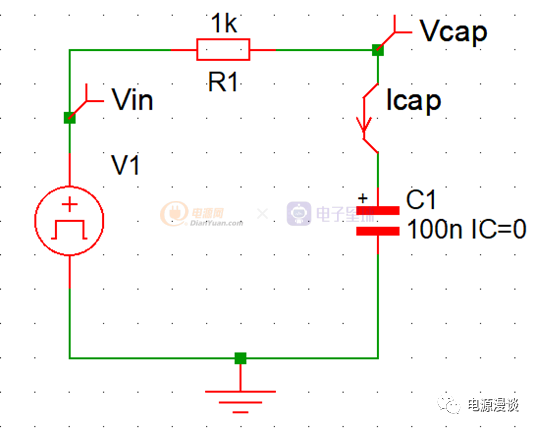
图3 电容充电过程仿真原理图
在一个容值为0.1u的电容上(初始电压为0V),串联一个1k电阻用于限流,然后施加一个电压幅值为5V的阶跃电压信号,以此模拟电容充电过程。我们观察阶跃电压Vin,电容电压Vcap,电容电流Icap的波形。
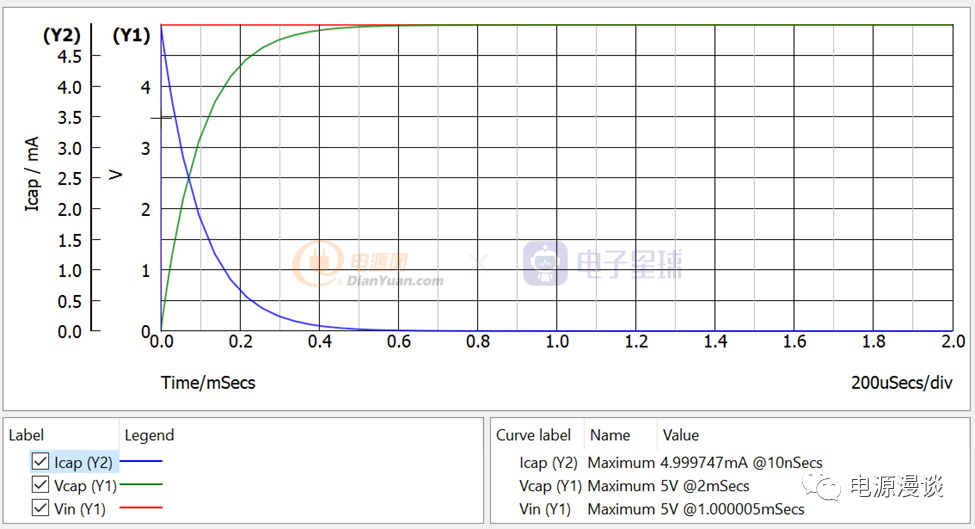
图4 阶跃电压给电容充电过程波形
通过仿真,我们可以看到,阶跃电压很快上升到5V,通过电阻1k给充电电流限流,因此在10ns处的电容电流最大接近5mA,即Vin/R1的值,绿色曲线为电压Vcap,其上升速度开始较快,后面逐步变慢,最终到接近输入电压5V。而对应的电容电流开始最大,后面逐步变慢,最后到0A电流。从仿真曲线上可以看出电容充电时电流取决于电压变化率,电压变化越快,充电电流越大。

图5 增大限流电阻时的阶跃电压充电过程波形
当我们增大限流电阻为3k时,则发现充电电流(蓝色实线所示)的最大值减小为了1.66mA,最终稳定到0A,充电电压(绿色实线所示)也变缓慢了很多,最终也是稳定到5V.
实际的电容的内阻(由寄生电阻ESR,引线电阻,电抗等组成)非常小,因此充电和放电过程都比较快,所以不能像高内阻的电池那样可以长时间充电和放电。放电过程和充电过程类似,我们就不再详述。
二.电容的交流输入特性分析
前面我们讨论的是电容上施加直流电压时的情况,接下来我们讨论一下电容上施加交流电压时的情形,看看电容在交流电压信号下的电压和电流关系。

图6 电容上施加交流电压信号示意图
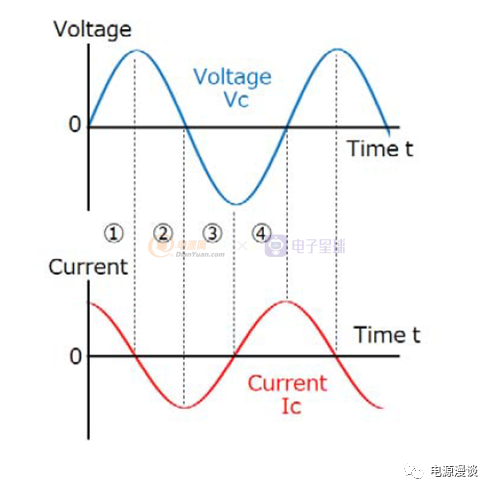
图7 交流输入电压信号下电容电压和电流关系
基于图6的电路下,可以得到如图7的波形,我们可以看到,电压蓝色曲线过零时,电流红色曲线的值最大,根据电容基本关系,这说明正弦电压过零时的电压变化率最快,而在电压蓝色曲线达到正或者负的峰值时,电流红色曲线是过零的,这说明在电压在峰值时电压变化率最小,因此电流也最低。
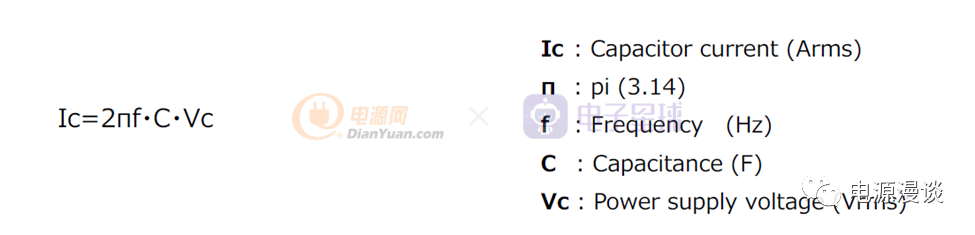
图8 电容电压和电流的频域关系
当我们在频域中分析电容的电压和电流关系时,由于在频域分析中s=jw,如图8所示,我们可以看出电流Ic会超前电容电压Vc90C的相位,这在上述图7的波形也可以得到验证,电压波形在90C(1/4正弦周期)之后,才和电容在0C时的波形一致。
接下来,我们通过仿真进一步验证其电压和电流关系。
图9 正弦输入电压源设置
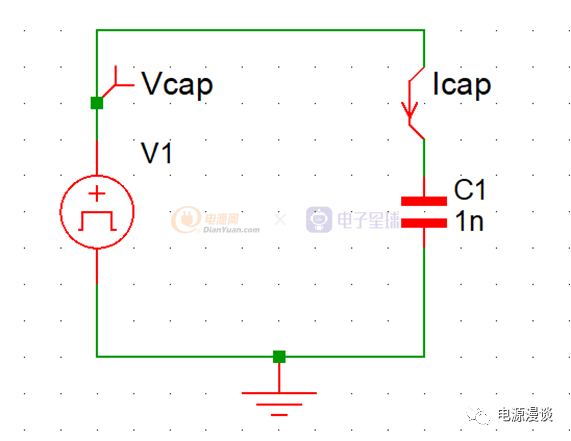
图10 电容交流输入特性仿真
我们在图10中的仿真中,以幅值为+-5V的正弦波为输入信号,频率为10k,电容为10n,我们观察其电流和电压关系。
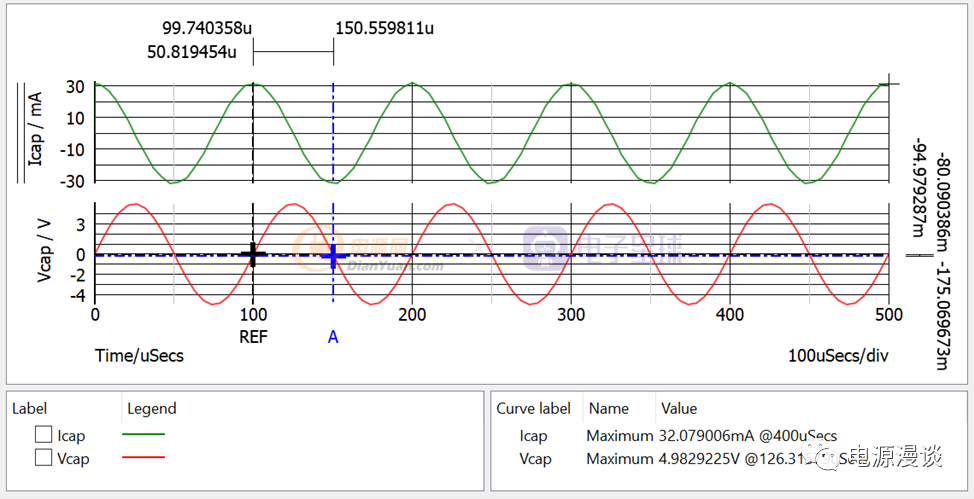
图11 交流输入信号下电容电压和电流关系
从图11仿真波形可以看到,红色曲线为交流输入信号正弦电压,绿色为得到的同频率的正弦电流信号,我们通过光标可以看到,当电压在过零时,对应电流的正或者负的峰值,电压上升时对应正电流峰值,电压下降时对应负电流峰值。
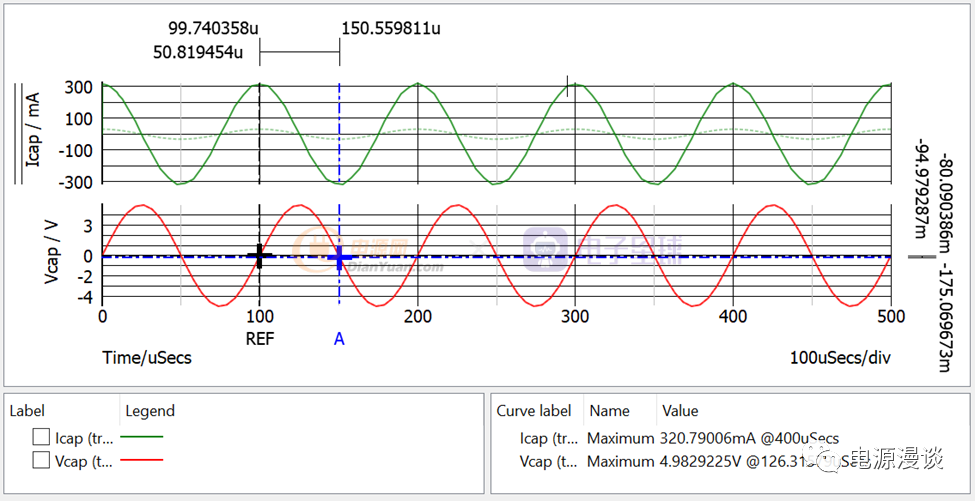
图12 电容变大时电压和电流关系
当我们将电容量从100n变到1u时,即增大10倍,发现电流和电压的相位关系不变,还是电流超前电压90C,但是峰值电流变大很多(实线部分),即说明电容量越大,电容阻抗越小,则电流越大,这一点通过图8的关系也可以看出来。
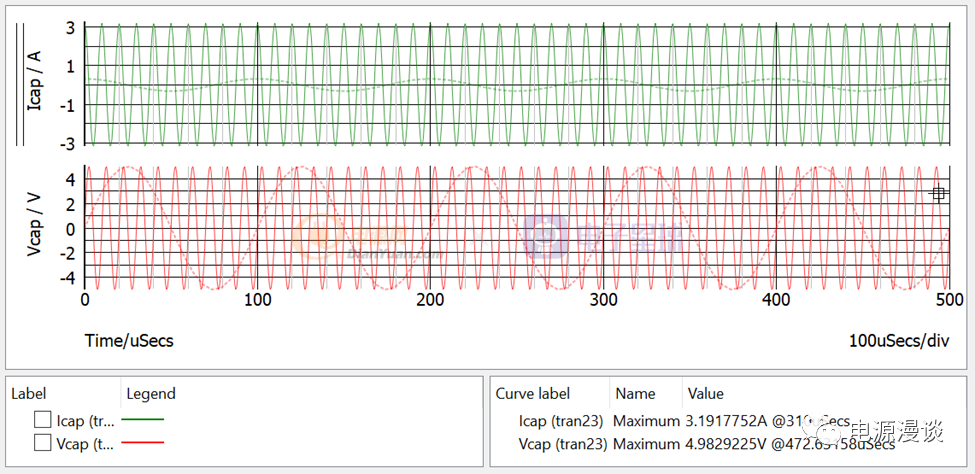
图13 提高信号频率时的电流电压关系
当我们将输入信号频率由10k改为100k后,仿真波形如图13所示,从图上看绿色曲线即电流变大为3.19A,这说明随着频率的提高,电容的阻抗变小,而输入电压幅值不变,则峰值电流(实线部分)变大。
三.电容在电路中的基本作用探讨
电容在电路中的作用主要是滤波,去耦,耦合等,我们接下来通过仿真进行说明。
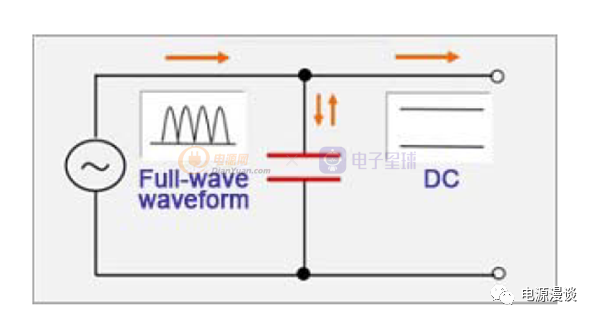
图14 电容的滤波作用分析
如图14中的电路一样,假定输入电压是一个交流正弦电压,经过整流桥整流为半波正弦,通过电容就可以将其大部分交流成分滤除,留下直流成分。
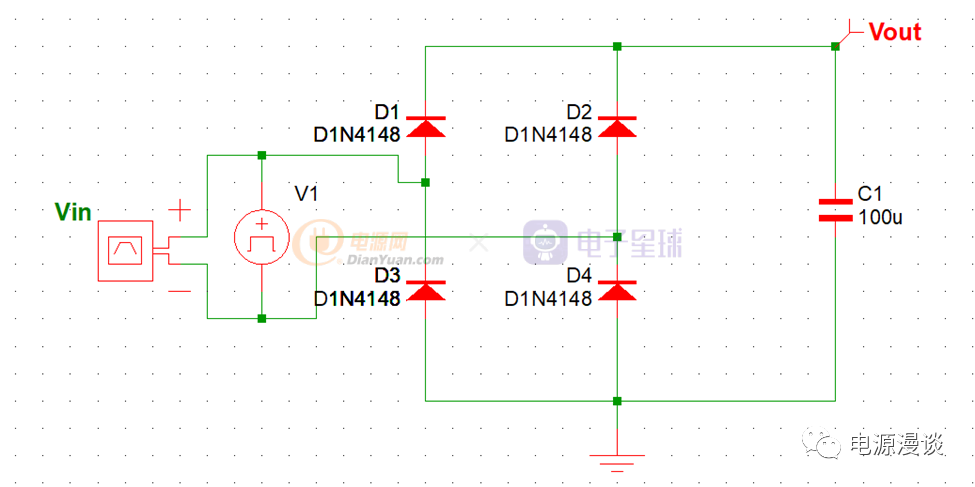
图15 电容平滑滤波仿真电路图
如图15设置仿真电路,输入信号为峰值+-5V的正弦波电压,频率为50Hz,经过整流桥整流后,被100u的电容滤波。我们观察输入信号电压波形,及输出电容波形。
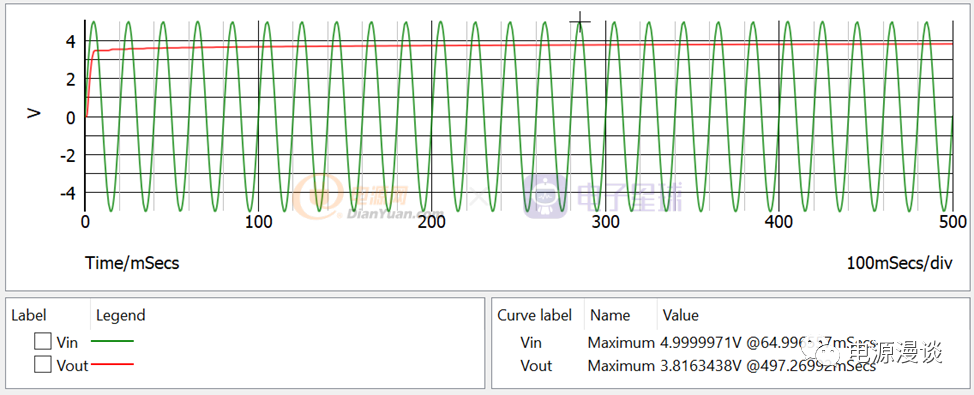
图16 电容平滑滤波仿真结果
在图16仿真结果中,我们可以看出,输出电容电压红色曲线被滤波为接近直流的电压,其幅值为3.8V.
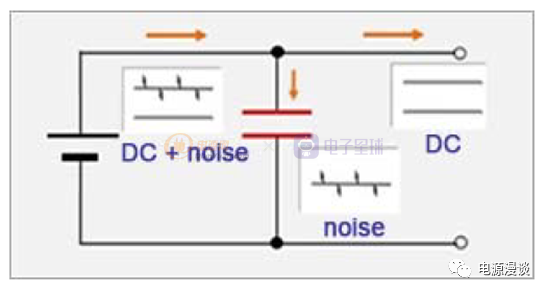
图17 高频噪声去耦
电容的另一个典型应用为高频噪声去耦,在直流电压中包含高频噪声的情况下,通过电容可以将高频噪声分离出去,而不让它达到电路的下一级。实际上,随着噪声频率的增加,在电容上的阻抗也随着降低,则高频噪声就分流到电容上面了,这就起到了噪声去耦的作用。
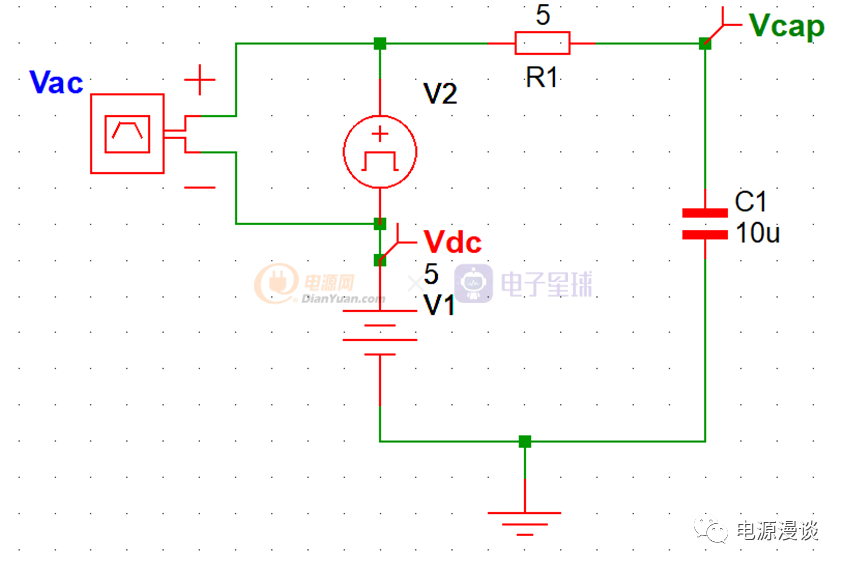
图18 电容的噪声去耦仿真
我们给出了噪声去耦的仿真原理图,如图18所示,在一个5V的直流电压上叠加了一个1MHz的高频噪声,幅值为+-200mV,我们观察电容滤波后的电压波形。
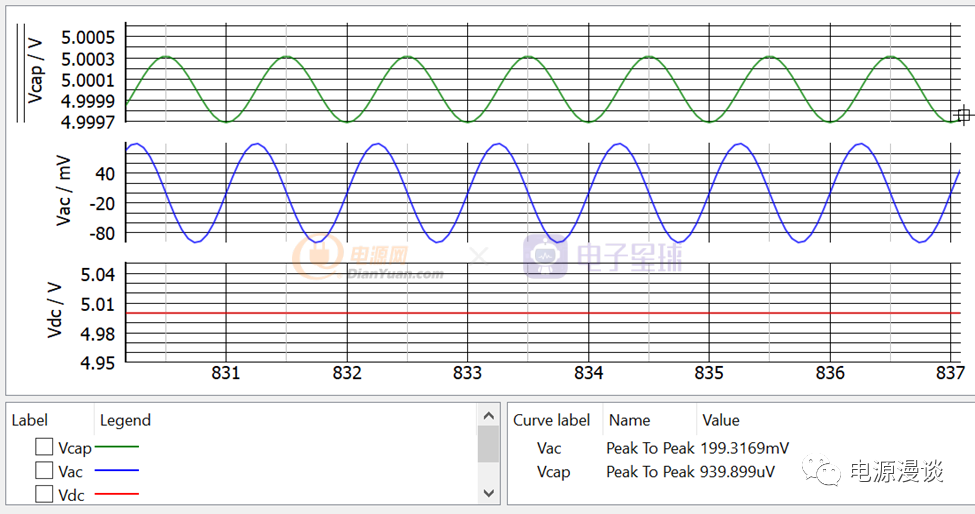
图19 电容噪声去耦仿真结果
我们在电路中串联5ohm电阻,模拟实际使用的情形,发现输入的噪声幅值+-200mv变为了滤波后的接近1mV。
电容还有一个典型的应用,就是通交隔直,当在电路中串联电容时,此时可以将叠加在直流信号中的交流信号耦合到电路的下一级,而直流信号不能通过,如下图20所示。
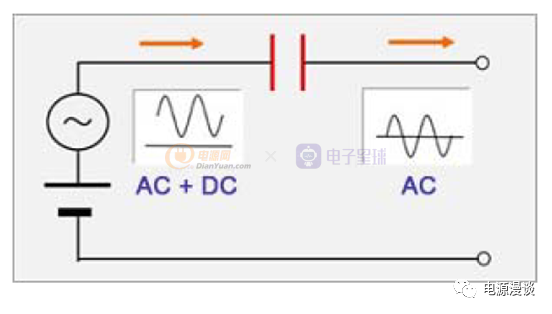
图20 电容隔直耦合作用
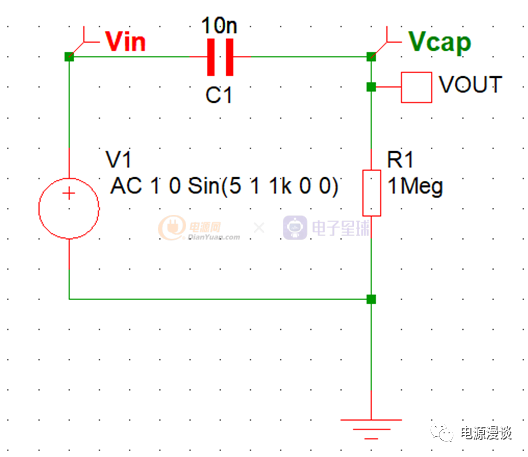
图21 电容交流信号耦合仿真原理图
如图21是我们的仿真原理图,输入信号为在5V直流信号上叠加了1k的交流信号,幅值为+-1V,经过串联耦合电容后,我们观察耦合电路的输出电压波形。
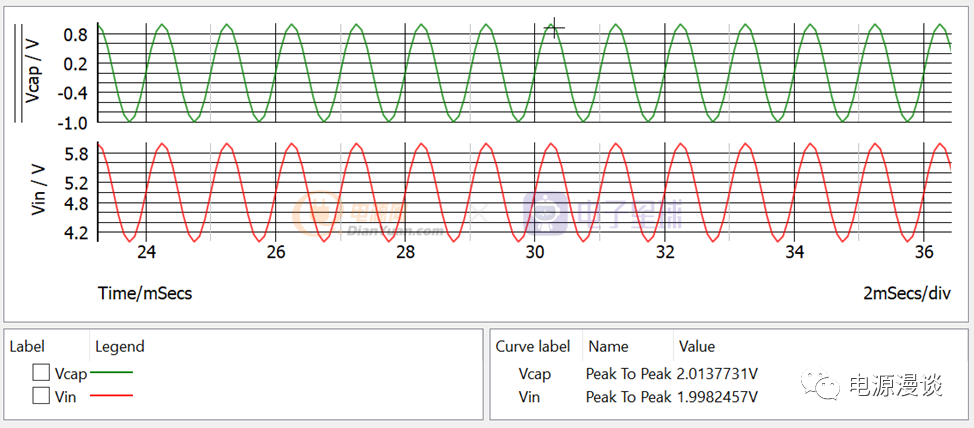
图22 电容交流信号耦合仿真结果
通过仿真,我们可知,输入信号中的交流信号被耦合到了电路输出端,而直流信号部分被去除了。
四.电容的寄生参数特性
理想电容的模型如图23左侧所示,但是实际上,其包含寄生串联电阻ESR,寄生串联电感ESL,也包含绝缘漏电流产生的电阻IR部分,如图23右侧所示。
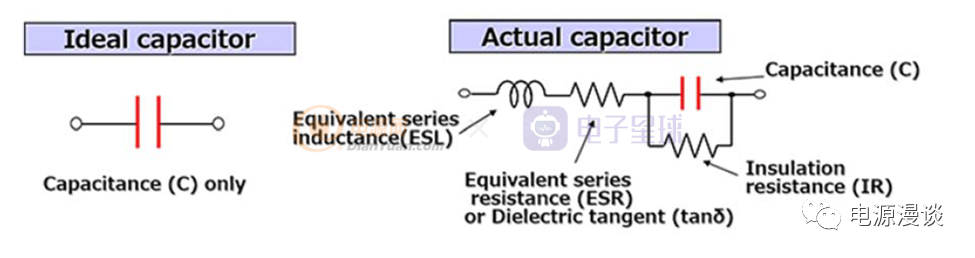
图23 电容参数模型
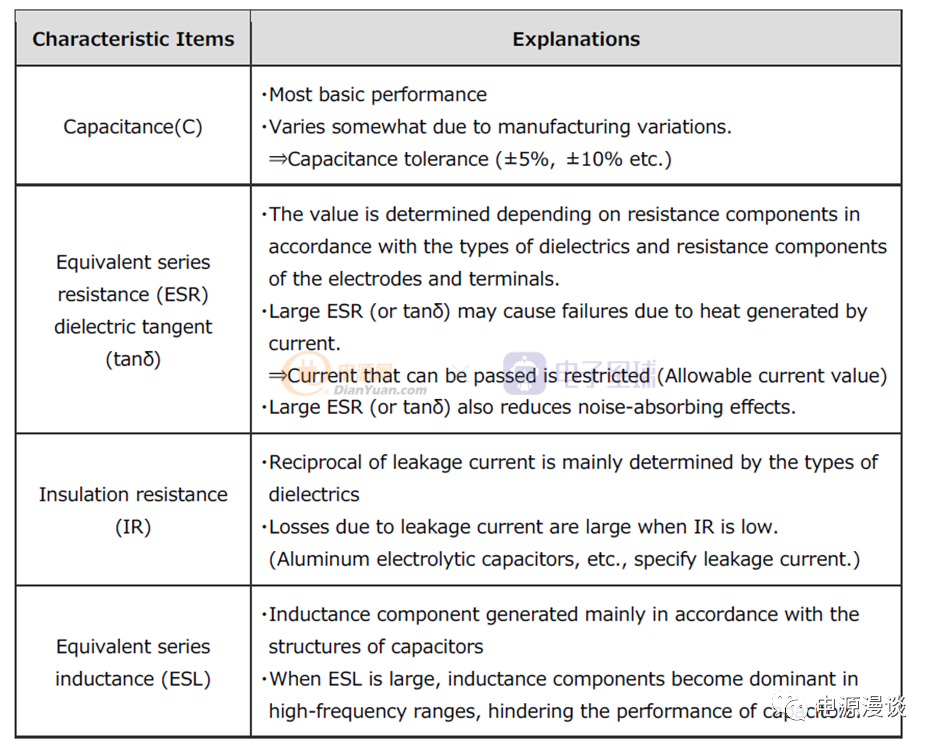
图24 电容参数说明
图24中我们给出了寄生参数的说明,从中我们可以看出,电容本身的电容量取决于生产制成,会标识一定的精度,如5%,10%等。
寄生电阻ESR的值取决于电介质的阻性分量,及电极和端部连接的阻性分量,太大的ESR会由于电流导致热失效,所以它允许的电流会被限制,同时大的ESR会影响噪声滤波性能,接下来我们通过仿真来说明。
漏电流主要取决于介电材质的类型,漏电阻比较小时的漏电流损耗会很大,铝电解电容,一般会指明漏电流是多少。
寄生电感ESL一般取决于电容的结构,当ESL较大时,在高频时ESL占主导地位,这会严重妨碍电容的滤波特性。

图25 电容在不同频率的阻抗值
当我们写出电容的阻抗关系时,如图25所示,我们会发现,电容的阻抗是随着频率变化,具有不同的表现的,低频阻抗主要取决于电容,高频阻抗取决于电感分量,谐振阻抗取决于ESR,我们接下来会通过计算得出结论。
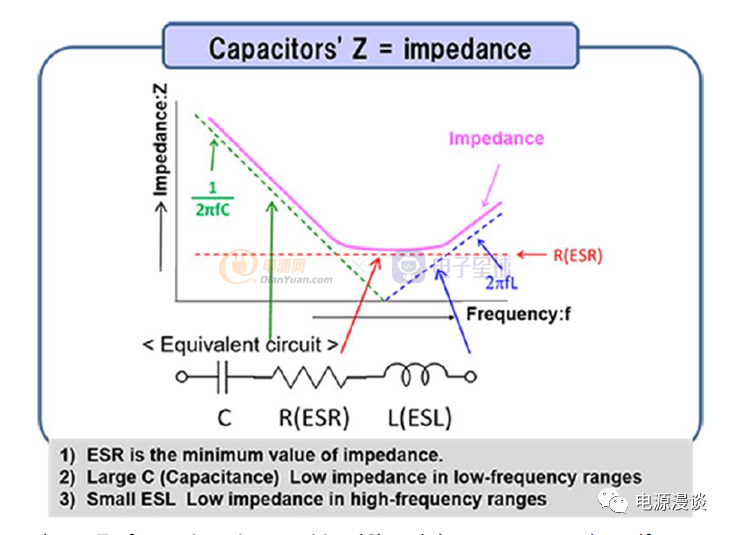
图26 电容阻抗的频率曲线
随着频率变化的电容阻抗曲线如图26所示,我们可以看到曲线的最小值就是电容的ESR,此时电容和电感阻抗相互抵消了,这个频率点对应电容的自谐振频率。
接下来,我们通过Mathcad计算电容的阻抗频率特性曲线。

图27 电容相关参数定义

图28 电容阻抗特性表达式

图29 电容阻抗及相位计算

图30 电容典型频率计算
计算求出ESR频率39.79k,及电容自谐振频率159k,如图30所示。
通过图27,28,29,我们求得电容阻抗随频率变化的曲线。
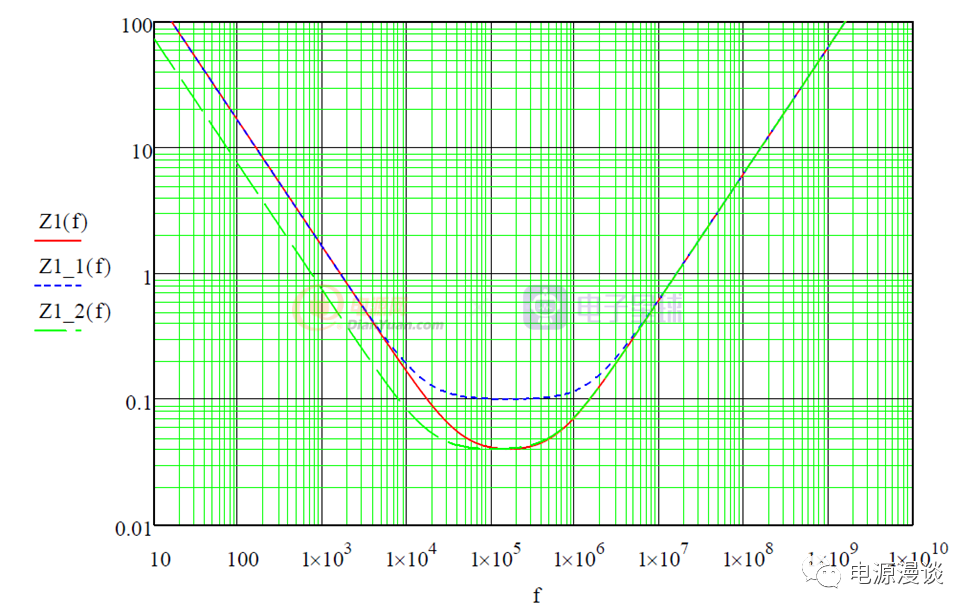
图31 电容阻抗特性曲线1
从图31所示电容阻抗曲线来看,随着ESR变大(对应Z1_1(f)),阻抗曲线的最小值提高,滤波衰减特性变差,随着电容值变大(对应Z1_2(f)),低频阻抗变低,滤波特性更好。
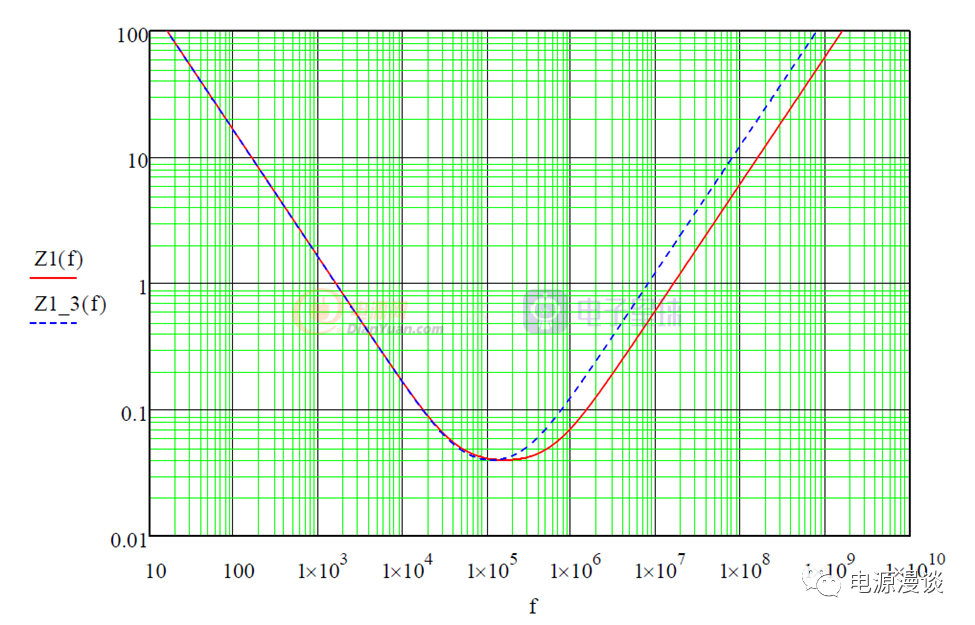
图32 电容阻抗特性曲线2
随着ESL寄生电感变大(对应Z1_3(f)),则高频的阻抗整体变高,高频滤波特性变差,且自谐振频率变低。
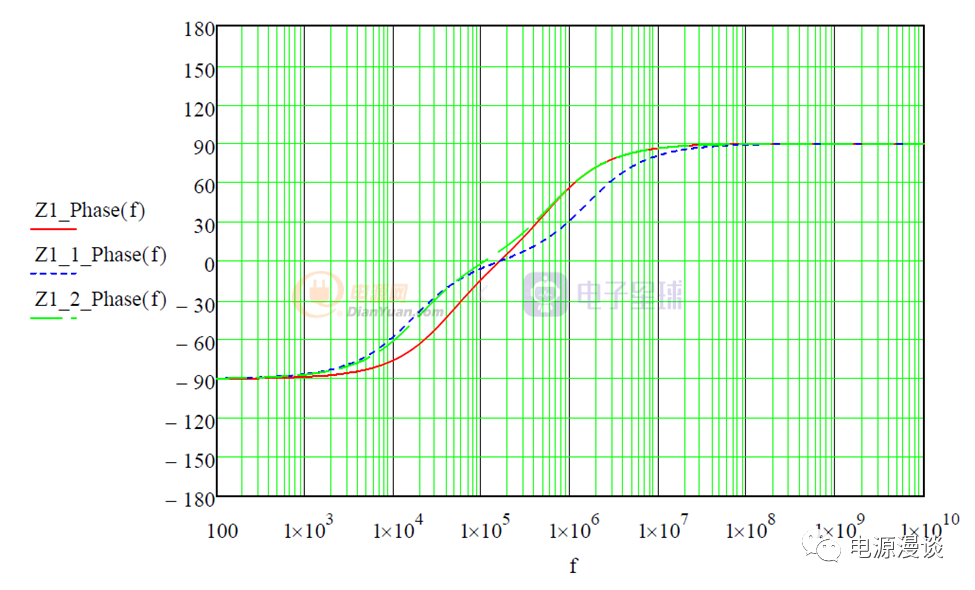
图33 电容相位曲线
从电容相位曲线来看,低频段由于电容占主要作用,相位为-90C,随着频率增加相位变为0,到了高频段,由于电感作用占主导,则相位变为90C,随着ESR及电容值变化,曲线形状发生一定变化。
由上述计算及分析可知,当使用电容做噪声滤波时,尽量让噪声频率和自谐振频率接近,同时尽可能的降低ESR及ESL,这样可以产生较好的滤波效果。
总结,上述文章通过分析电容的基本结构及基本时域特性,同时分析了电路中电容的典型作用,最后通过频域关系推导电容的阻抗来得出电容噪声滤波时的参数选择方向,通过以上可以对电容的基本特性有一定了解,有助于实际电路设计优化。
参考文章:Basic Knowledge of Capacitors,Panasonic


