状态空间平均法在开关电源功率级建模中应用非常广泛,但是状态空间法一般都涉及到大量的矩阵运算,手动运算即麻烦又容易出错,但在Mathcad中使用矩阵的符号运算功能,能轻松的完成这些复杂的计算,下面就以一个例子来介绍。
状态空间平均法是用矩阵的方式描述开关电源系统,然后根据小信号近似和线性化等效的原则进行简化,进行矩阵运算,得到系统的传递函数的一种方法。
这种方法的优点是:建模的思路清晰,不需要做复杂的电路变换;通用性强,对于PWM控制的电路拓普都适用。
缺点:手动运算非常繁杂,容易出错。
对于线性定常系统来说,通常可以用下面一组方程来描述:

其中X为状态向量,一般选择在开关切换时不会突变的物理量,如储能元件的电流或电压。在这里选择电感电流iL和电容电压uc。
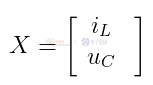
U为输入向量,一般会选择输入电压vg
Y为输出向量,选择输入电流ig和输出电压vout。
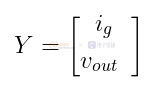
然后进行进行小信号近似和线性等效,具体过程不再详述,可以自行在网上查找。
boost非理想电路
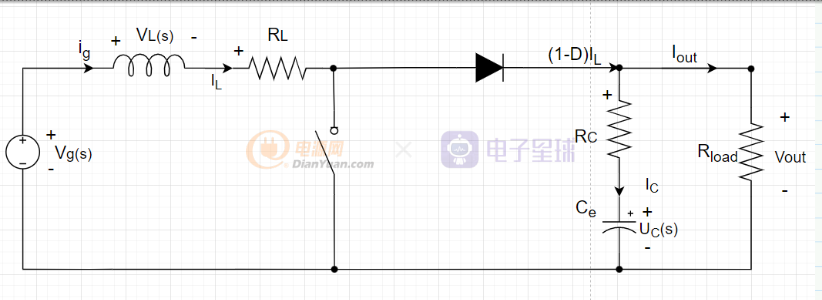
当开关管导通时,可以得到下列一组方程:

用Mathcad符号求解的命令solve解方程组,可得:

再化简成标准形式:

得到diL/dt和duC/dt的值:

再看boost的原理图,还可以得到另外一组方程:
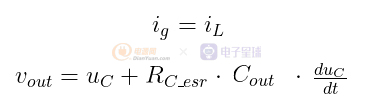

所以可以得到一组A1、B1、C1和E1的矩阵:

当开关管关断时,再得到下面的方程:

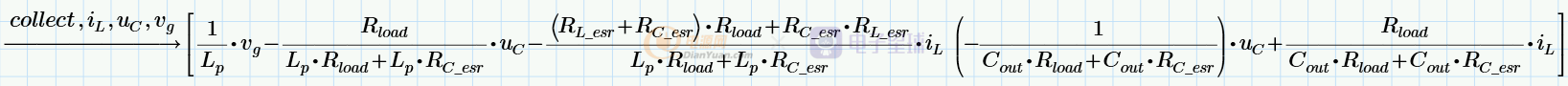

求出一组矩阵

再根据公式可得:

求得状态向量直流工作点函数关系(vg为输入电压的直流分量,D为占空比的直流分量):

如果忽略电感和电容的等效串联电阻可得到:
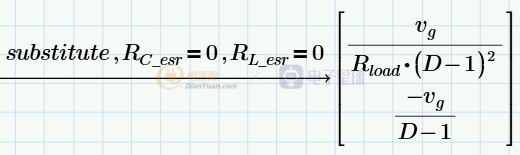
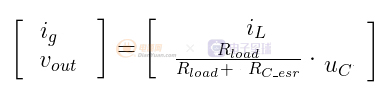
求得输出向量直流工作点函数关系(Ig为输入电流的直流分量,Vout为输出电压的直流分量):

如果忽略电感和电容的等效串联电阻可得到:

从上面的结果中,可以很方便的得到电感电流IL、电容电压Uc、输入电流Ig和输出电压Vout分别与输入电压Vg的直流量关系。
分析上面的结果可知:对于直流量来说,电感电流IL等于输入电流Ig*D,电容电压uc等于输出电压Vout。
经过线性化等效后,有(x为X向量的小信号交流分量,y为Y向量的交流分量):

可以得到boost功率级参数对输入电压vg(s)的传递函数:

因为结果过长,无法完整展示出来,只能显示一部分。忽略电感和电容的等效串联电阻,并用D=1-D`替代后,得到:

vout(s)/vg(s)即输入电压对输出电压的影响,例如输出电压的低频纹波主要由该传函决定。
ig(s)/vg(s)的倒数即为boost的输入阻抗。
再求得boost功率级参数对占空比d(s)的传递函数:
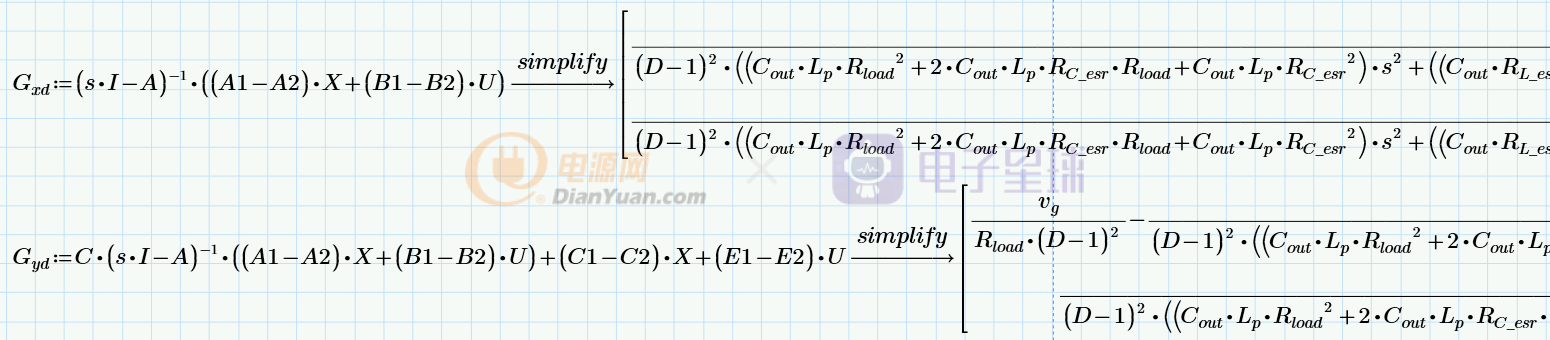
简化后,得到结果:

iL(s)/d(s)在做电流型控制时经常会用到。
vout(s)/d(s)在做电压型控制时经常会用到。
到此,几乎得到所有功率级的传递函数,配合不同的控制方式,可以得到系统的整体的传递函数,来进行环路的设计工作。
本文涉及的计算文件,在附件中提供。文件用Mathcad Prime 8.0编写。


