一般数字控制器设计方法采用直接数字法：s域的被控对象首先被转化到z域，控制器设计直接在z域中进行。当然，也有另外一种数字再设计方法，控制器在s域中设计，然后再进行离散化。在数字再设计法中，当采样频率足够高时，由数字控制的采样保持过程导致的时间延迟可以做一个近似表达。在时间延迟环节被线性化以后，就可以根据系统的性能指标在s域中采用Bode图之类的标准设计方法来设计模拟控制器，一旦模拟控制器被设计出来以后，就能够被离散化。
s域到z域的离散化方法建议采用双线性变换，也就是tustin变换：
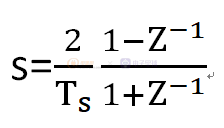
双线性变换法把s域的整个左半平面映射为z平面的单位圆，因而不会影响离散化后系统的稳定性，除此之外，双线性变化发最吸引人的特征是在低于1/10采样频率时同时保留了控制器幅值和相位的频率特性。与被控对象校正后系统开环传递函数的幅值穿越频率相比，当采样频率足够高时，可以采用数字再设计法。
现在以一个s域的补偿器设计为例，流程如下：
1）首先选择一个合适的已知原型滤波器传递函数（要选择合适的零极点）；
以3p3z补偿器为例，其常见表达式为：
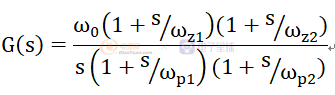
上述补偿器提供一个零极点，以提高低频增益；提供两个零点wz1和wz2，提供两个极点wp1和wp2.假设提供零点频率800Hz,两个零点 分别为300Hz和900Hz，两个极点分别为500Hz和5KHz，可以如下表达：
2）将改原型滤波器的s域传递函数映射到z域中；
可以利用matlab将上述s域方程进行z域的转换，matlab变换程序如下
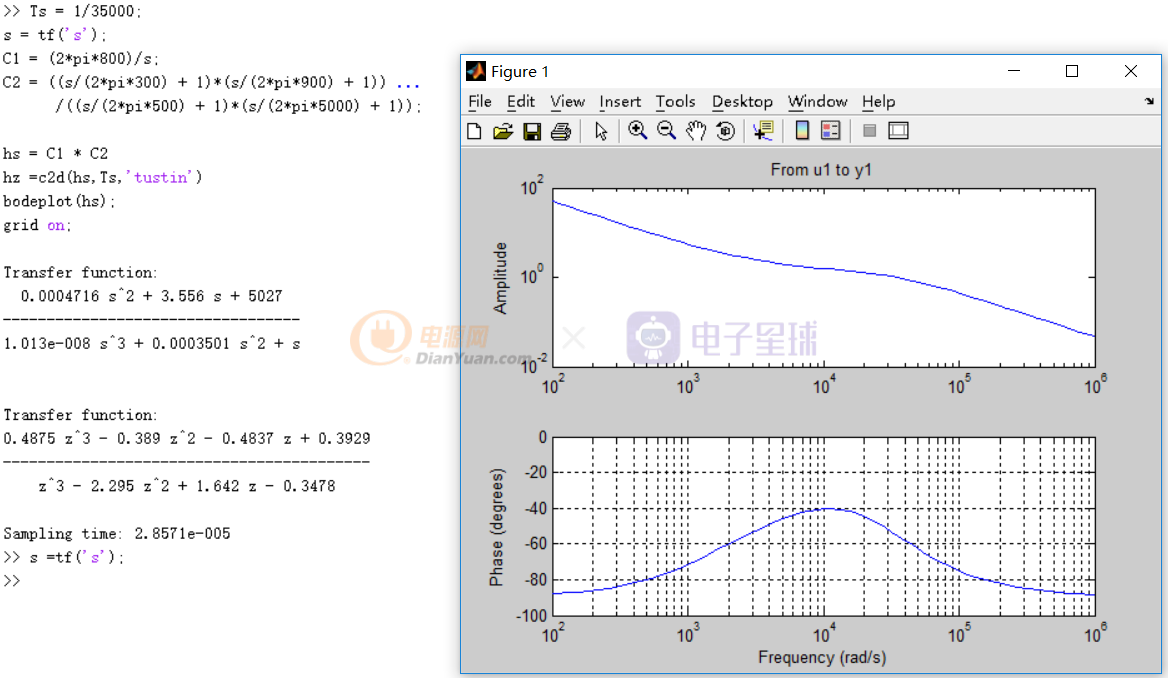
现在得到了z域的表达式为：
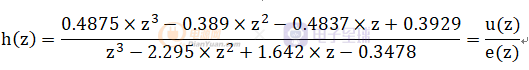e(z)是误差量，u(z)为输出量。
另外举例为一个SZSP的s传递函数如下（极点频率在10Hz,零点频率在250Hz）：
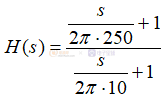
利用matlab变换如下（采样频率100kHz）：
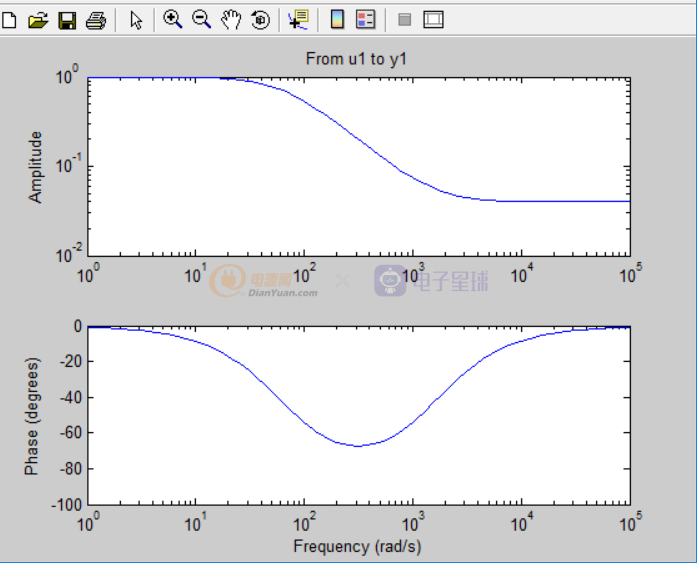
除了matlab可以进行方便快捷的变换之外，数学软件Mathcad也是可以的
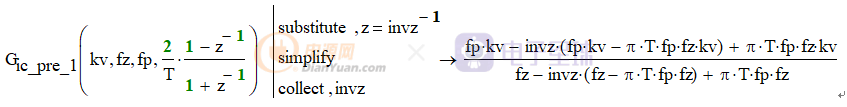
3）将z域转换为时域内的线性差分方程；
由于dspic33系列是16bit定点，所以需要对A/B系数进行Q15定标然后再进行计算。
在MCU内部执行方式如下：
