从以往的仿真经验来看,单相逆变器仿真是一个简单、不需要太多计算与调试就可以实现基本正弦波的输出。如果输出电压不理想,调整调整载波频率、电感、电容也可以勉强的输出正弦波。但是当涉及到逆变器的闭环控制、三相逆变器的开环闭环仿真时,会发现调试变得困难,瞎凑参数也凑不出理想的波形。复杂一些涉及到并网逆变器、直接功率控制等控制方法的仿真更是难上加难。此时就会想到数学模型的魅力。根据计算的数学模型、传递函数、设计闭环环路控制才是王道。因此从简单的单相逆变器重新开始学习。本次学习不注重逆变器原理的仿真,主要学习一些关键公式的推到,并通过仿真的形式验证关键公式。
1 单相逆变器的基本原理
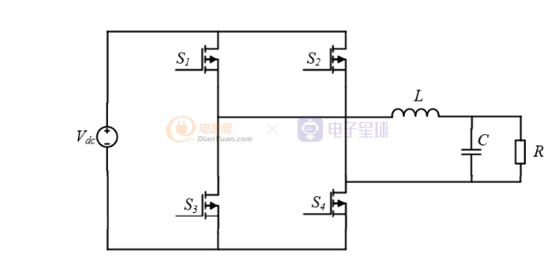
简单介绍一下工作原理:
在SPWM调制下,1、4互补导通,2、3互补导通。1、4导通输出+Vdc,2、3导通输出-Vdc。14、23导通时间由SPWM调制计算得出。所以可以将你便电路进行简化,简化电路如下:
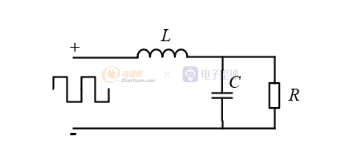
可以把逆变电路分为两个部分。1 SPWM波产生电路 2 LC滤波电路
SPWM波产产生的是方波,逆变电路想要输出的是一个正弦波。两者除了在波形上有差距,最本质的差距就是方波内包含想要输出的正弦波以及不想要输出的杂波。这个杂波就是谐波。
LC滤波器,就起到把其余杂波滤掉的功能,同时不能滤掉我们希望得到的波形。
所以就需要搞清楚三个问题。
1 我们想要输出的正弦波是什么。如何确定SPWM方波内包含期望输出的正弦波?
2 SPWM方波内除了期望的正弦波,还包含什么样的波?
3 LC滤波器能滤除什么样的波?
问题1:
SPWM调制的原理:将期望输出电压作为调制波,将高频三角波作为载波,将调制波与载波进行比较。当调制信号大于载波信号时,逆变器输出电压为正,当调制信号小于载波信号时,逆变器输出电压为负。这个过程就是调制。PWM调制的基础原理:对于具有惯性的环节而言,如果多个窄脉冲的面积(冲量)相等,即使它们的形状不同,这些窄脉冲加在环节上的效果也是基本相同的。
通过PWM调制就可以将调制波这个模拟信号转化为数字信号。模拟信号就是一个连续的波形。而转化呈的数字信号是一个仅包含0 1的信号,表现形式就是一个方波。而方波的脉冲的宽度就包含着那个模拟信号的信息。我们调制波为我们期望输出的波形,SPWM调制出来的SPWM方波内就包含着我们期望输出波形。
问题2
SPWM方波的谐波含量。
根据傅里叶变换可知,每一个周期性的信号,都是由不同频率、幅值、相位的正弦波组成。因此可以根据傅里叶的理论分析出SPWM波内的波形组成,这个过程就是傅里叶变换。傅里叶变换可以通过傅里叶展开式计算,(我也尝试学着推到SPWM方波傅傅里叶展开式,但没有找到具体的推导过程。自我感觉就算找到也不理解),本文不对详细推导过程做过多阐述,仅借用文献[1][2]的结果 ,后续将通过仿真全方面验证SPWM方波的谐波含量。

文献[1]基于MATLAB的单相SPWM逆变电路谐波分析-付江梦
文献[2]SPWM单相逆变电路的谐波分析-胡赛纯


