一、滤波器基础
1.1、滤波器定义:
《GB/T 2900.1-2008电工术语 基本术语》定义:滤波器(Filter)是指按规定的法则设计用来传递输入量的各频谱分量的一种线性二端口器件。通常是为了通过某些频带频谱分量而衰减在其它一些频带内的频谱分量。
滤波器的通用定义:滤波器是集中参数的电阻、电容和电感,以及分布参数的电感、电容构成的网络。这种网络允许某些频率通过,对其它的频率成分加以抑制衰减,滤波器实际上是选频电路。

简单的电源滤波器设计
1.2、滤波器分类:
1.2.1、根据频率特性(幅频特性与相频特性)
可分为低通滤波器、高通滤波器、带通滤波器、带阻滤波器。
低通滤波器:
从0~f2频率之间,幅频特性平直,可以使信号中低于f2的频率成分不受衰减地通过,而高于f2工的频率成分受到极大地衰减。
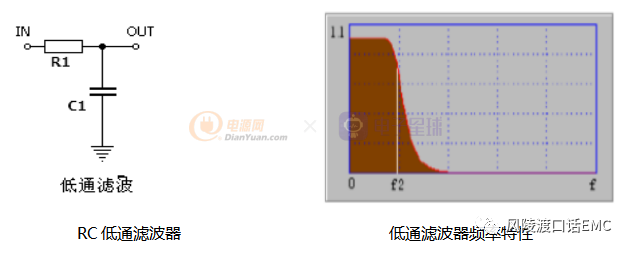

低通滤波器主要电路形式
高通滤波器:
与低通滤波器相反,从f1~∞频率之间,其幅频特性平直,使信号高于f1的频率成分几乎无衰减的通过,而低于f1的频率成分将受到极大地衰减。
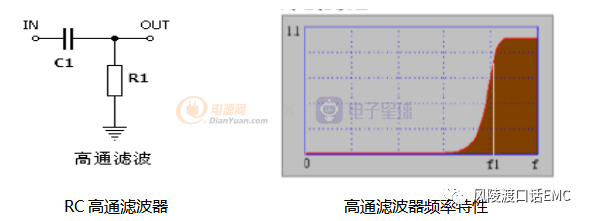
带通滤波器:
在通频带f1~f2之间,它使信号中高于f1而低于f2的频率成分可以不受衰减地通过,而其它成分受到衰减。
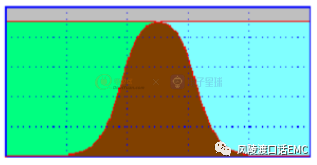
带通滤波器频率特性
带阻滤波器:
与带通滤波器相反,阻带在频率f1~f2之间,它使信号中高于f1而低于f2的频率成分受到衰减,而其它频率成分的信号几乎不受到衰减地通过。
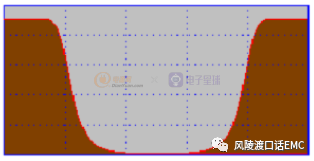
带阻滤波器频率特性
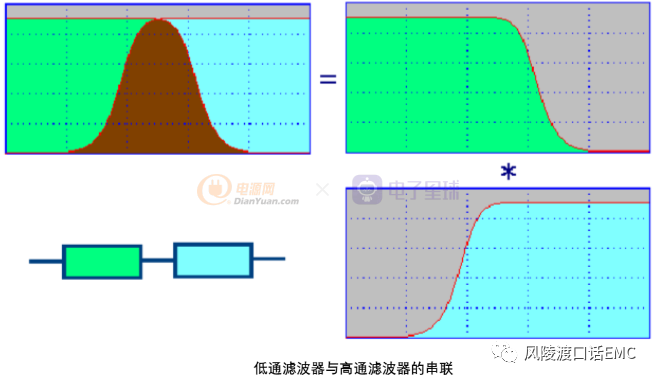
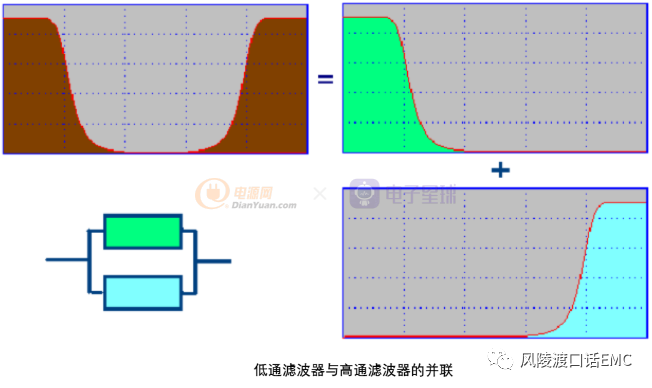
低通滤波器和高通滤波器是滤波器的两种基本形式,其它的滤波器都可以分解为这两种类型的滤波器,低通滤波器与高通滤波器的串联为带通滤波器,低通滤波器与高通滤波器的并联为带阻滤波器。
1.2.2、根据能量损耗特性
可分为反射式滤波器和吸收式滤波器。
反射式滤波器:
反射式滤波器又称无损滤波器,其工作原理是在电磁信号传输路径上形成很大的特性阻抗不连续,使大部分电磁能量反射回信号源处。反射式滤波器采用电感L、电容C等储能元件组成的无源网络,有很好的频率选择特性,但容易产生谐振。
吸收式滤波器:
采用有损耗的滤波元件,使骚扰信号的能量消耗在滤波器中,以达到抑制干扰的目的,又称有损滤波器,吸收式滤波可避免反射式滤波因寄生参数效应或阻抗不匹配引起的谐振,但其频率选择性较差。吸收式滤波器采用铁氧体材料或其他有损耗材料,将导线穿过或缠绕在各种形状的铁氧体材料上,利用其电感及磁场涡流损耗阻断骚扰信号的传播。
1.2.3、根据"最佳逼近特性"标准分类
可分为巴特沃斯滤波器、切比雪夫滤波器、贝塞尔滤波器。
巴特沃斯滤波器(Butter worth Filter):
从幅频特性提出要求,而不考虑相频特性。巴特沃斯滤波器具有最大平坦幅度特性,特点是通频带内的频率响应曲线最大限度平坦,没有纹波,而在阻频带则逐渐下降为零。
巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示:
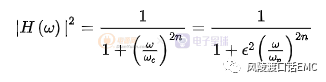
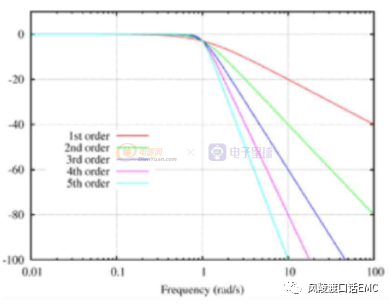
巴特沃斯1~5阶低通滤波器曲线
切比雪夫滤波器(Cheby shev Filter)
切比雪夫滤波器,又名"车比雪夫滤波器",是在通带或阻带上频率响应幅度等纹波波动的滤波器。切比雪夫滤波器来自切比雪夫分布,是用以纪念俄罗斯数学家巴夫尼提.列波维其.切比雪夫。
切比雪夫滤波器在过渡带比巴特沃斯滤波器的衰减快,但频率响应的幅频特性不如后者平坦。切比滤波器和理想滤波器的频率响应曲线之间的误差最小,但是在通频带内存在幅度波动。
I型切比雪夫滤波器,切比雪夫滤波器的幅度与频率的关系可用下列公司表示:
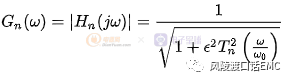
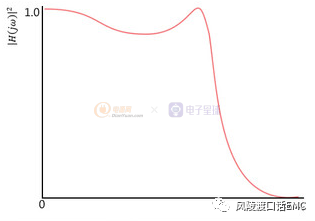
I型切比雪夫滤波器函数曲线
II型切比雪夫滤波器:
也称倒数切比雪夫滤波器,较不常用,因为频率截止速度不如I型快,也不需要用更多的电子元件。II型切比雪夫滤波器在通频带内没有幅度波动,只在阻带内有幅度波动。
II型切比雪夫滤波器的转移函数为:

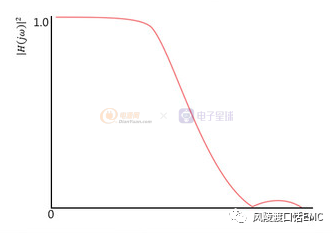
II型切比雪夫滤波器函数曲线
贝塞尔滤波器(Bessel Filter):
贝塞尔滤波器是具有最平坦的幅度和相位响应。带通的相位响应近乎呈线性。贝塞尔滤波器由于具有向其截止频率以下的所有频率提供等量延时的特性,才被用于音频设备中,在音频设备中,必须在不损害频带内多信号的相位关系前提下,消除带外噪声。描述贝塞尔滤波器低通滤波器的传递函数如下:
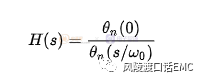
1.2.4、滤波器其它分类方式

二、滤波器非理想性
2.1、理想滤波器:
理想滤波器是指能使通带内信号的幅值和相位都不失真,阻带内的频率成分都衰减为零的滤波器,其通带和阻带之间有明显的分界线。也就是说,理想滤波器在通带内的幅频特性应为常数,相频特性的斜率为常数,在通带外的幅频特性为零。
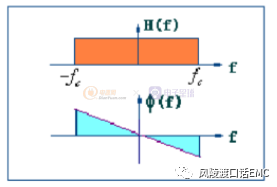
理想滤波器的幅频与相频特性
2.2、实际滤波器:
理想滤波器是不存在的,在实际滤波器的幅频特性图中,通带和阻带之间应没有严格的界限。在通带和阻带之间存在过渡带,在过渡带内的频率不会被完全抑制,只会被衰减。滤波器设计时希望过渡带越窄越好,也就是希望对通带外频率成分衰减的越快越好,实际滤波器设计时,总是通过各种方法使其尽量逼近理想滤波器。
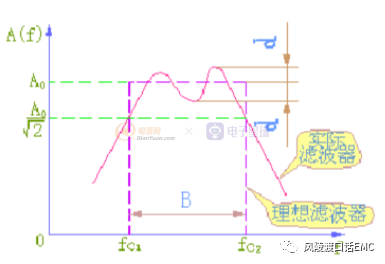
理想滤波器与设计滤波器幅频特性对比
三、滤波器的技术参数
滤波器的主要参数:插入损耗、回波损耗、通带带宽、带内波动、纹波、带内驻波比、中心频率、截止频率、延迟、带内相位线性度。
3.1、插入损耗(Insertion Loss):
由于滤波器的引入对电路中原有信号带来的衰减,以中心或截止频率处损耗表征,如要求全带内插损需要强调。插入损耗是衡量滤波器的主要指标参数,插入损耗是不带滤波器时,从源端到负载转换的信号电压与加入滤波器时源到负载转换的信号电压的比值:
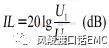
U1-----未接入滤波器,信号源在负载上建立的电压。
U2-----接入滤波器,信号源在负载上建立的电压。
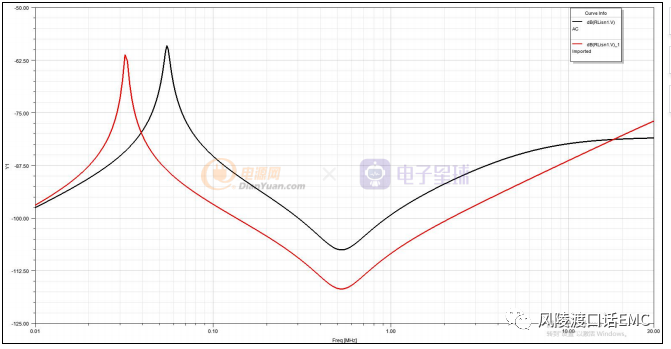
滤波器插入损耗仿真曲线图
3.2、回波损耗(Return Loss):
又称为反射损耗,是表示信号反射性能的参数,回波损耗说明入射功率的部分被反射回到信号源。回波损耗主要是链路中阻抗不匹配所产生的,回波损耗与反射系数的关系为:
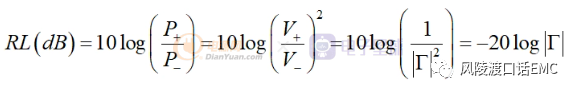
回波损耗愈大愈好,以减少反射信号对系统的影响,输入功率被全部吸收时回波损耗为无穷大。
3.3、阻抗特性:
滤波器的输入阻抗、输出阻抗直接影响其插入损耗特性。在使用EMI滤波器时,保证在输入、输出最大限度阻抗失配的情况下,有合乎要求的最佳抑制效果。使用信号滤波器,应遵循对有用信号输入、输出端阻抗匹配原则,防止信号衰减,对无用信号或需要滤除的干扰信号来说应保证最大阻抗失配,达到最佳滤波效果。
滤波器阻抗仿真曲线图示:
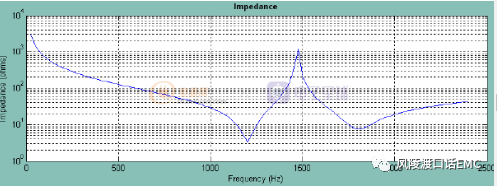
根据源阻抗与负载阻抗选择滤波器:
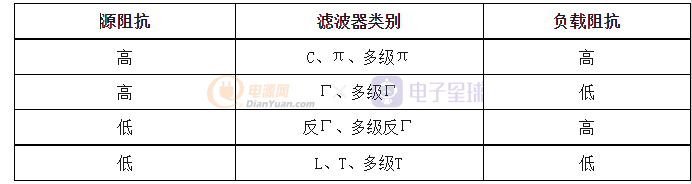
滤波器要满足负载电路工作频率和需抑制频率的要求。在所要求的频率上,滤波器的阻抗必须与它连接的干扰源阻抗和负载阻抗匹配,如果干扰源是高阻抗,则滤波器的输出阻抗应为低阻;如果干扰源是低阻抗,则滤波器的输出阻抗应为高阻。
3.4、其它参数指标:
3.4.1、延迟(TD):
指信号通过滤波器所需要的时间,数值上为传输相位函数对角频率的导数,即TD=DF/DV。
3.4.2、纹波(Ripple)
指3dB带宽(截止频率)范围内,插损随频率在损耗均值曲线基础上波动的峰-峰值。
3.4.3、带内波动(Pass Band Ripple):
通带内插入损耗随频率的变化量。1dB带宽内的带内波动是1dB。
3.4.4、带内驻波比(VSWR):
衡量滤波器通带内信号是否良好匹配传输的一项重要指标。理想匹配VSWR=1:1,失配时<1。在入射波和反射波相位相同的地方,电压振幅相加为最大电压振幅VMAX,形成波腹。
在入射波和反射波相位相反的地方电压振幅相减为最小电压振幅VMIN,形成波节。其它各点的振幅值则介于波腹与波节之间,这种合成波称为行驻波,驻波比是驻波波腹处的电压幅值VMAX与波节处的电压幅值VMIN之比。
3.4.5带内相位线性度:
该指标表征滤波器对通带内传输信号引入的相位失真大小。按线性相位响应函数设计的滤波器具有良好的相位线性度。
3.4.6、截止频率(Cutoff frequency):
指低通滤波器的通带右边频点及高通滤波器的通带左边频点,通常以1dB或3dB相对损耗点来标准定义。相对损耗的参考基准为:低通以DC处插损为基准,高通则以未出现寄生阻带的足够高频带频率处插损为基准。
3.4.7、中心频率(Center Frequency):
滤波器通带的频率为f0,一般取f0=(f1+f2)/2,f1、f2为带通或带阻滤波器左、右相对下降1dB或3dB边频点。窄带滤波器常以插损最小点为中心频率计算通带带宽。
四、滤波器的安装要求:
4.1、滤波器安装位置要求:
- 一个骚扰源影响多个敏感设备时,滤波器靠近骚扰源放置。反之,只有一个敏感设备,而有多个骚扰源时,滤波器靠近敏感设备放置。滤波器靠近骚扰源放置的好处,使干扰局限在骚扰源附近,切断骚扰源的干扰路径,抑制骚扰源的发射。
- PCB上滤波器应安装在接口处,需要安装多个滤波器时,应并列安装,防止不同信号线滤波前后的耦合;当信号接口处只有一个干扰源时,滤波器应尽量靠近骚扰源安装 。
4.2、滤波器输出输入布线要求:
- 滤波器的输入与输出线必须屏蔽隔离,输入与输出布线靠近时会互相耦合,降低滤波器的滤波效果。
- 其它信号布线应避免贴近需要增加滤波器的干扰信号布线放置,避免干扰信号源耦合到其它信号布线,降低滤波器的滤波效果。
- 滤波后的信号布应避免靠近强干扰信号布线,避免滤波后信号线被二次污染,降低滤波器的滤波效果。
4.3、滤波器的接地要求:
- 滤波器通过细地线接地,高频滤波效果非常差,使滤波器的接地外壳与金属结构平面良好搭接,改善接地效果。
- 滤波器接地点应选择静地(无强干扰源污染的地平面),接地线应尽量短而粗,减小接地的寄生电感,且接地点应选择回流干扰源环路面积最小的点。


