稳定性需要对补偿电路 G(s) 进行整形,以便在选定的交叉点提供足够的相位裕度以及直流的高增益。 为此,可以使用多个补偿电路,组装极点和零点。 我们通常需要的是在交叉频率处进行相位提升以提供正确的相位裕度。 这是通过强制环路在交叉频率附近以-1 斜率或-20 dB/十倍频程进行交叉来实现的。 然而,有时所需的提升太大,以至于无法达到想要的分频频率。此时,必须修改补偿目标并采用一个更合适的目标。让我们先回顾一下关于无源滤波器的基础知识,然后是基于运算放大器的电路环路补偿设计。
一、无源--单极点
我们最常见的RC滤波器就是一个很好的极点,图1 表示产生所谓的无源单极响应的 RC 电路。 也称为低通滤波器,它会随着频率的增加而引入相位滞后(或延迟)。 其拉普拉斯传递函数具有以下形式:
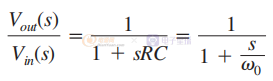
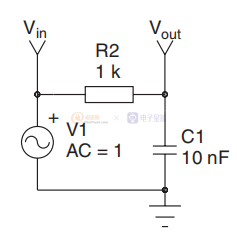
图1
该无源滤波器的截止脉动,即当直流“增益”降低 3 dB 时,由经典公式给出:
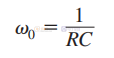
我们就可以画出该RC电路的bode图:

图2
通常在补偿电路中插入一个单极点,以在某个点滚降增益。幅度下降的速率为 –20 dB/十倍频。 也就是说,在截止频率之后,频率f1和f2处,其中f2=10f1幅度差为 20 dB,其中 为 20 dB。在波特图上,这显示为“-1”斜率,而 -40 dB/十倍频电路( 通常是二阶网络)的斜率为“-2”。
二、无源--单零点
如果传递函数包含零,则它出现在分子 N(s) 中。 在零频率下,分子取消传递函数并使之归零。 描述了零的广义形式:
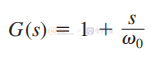
这样的表达式描述了 0 dB 的直流“增益”,然后是在零位置出现的+20 dB/十倍频程斜率(+1 斜率)。 相位现在为正,如图3 所示。这是与“滞后”相位的极点相比,实际上“提升”相位的零的特性。 因此在 G(s) 中引入零以补偿功率级响应中出现的过度相位滞后。
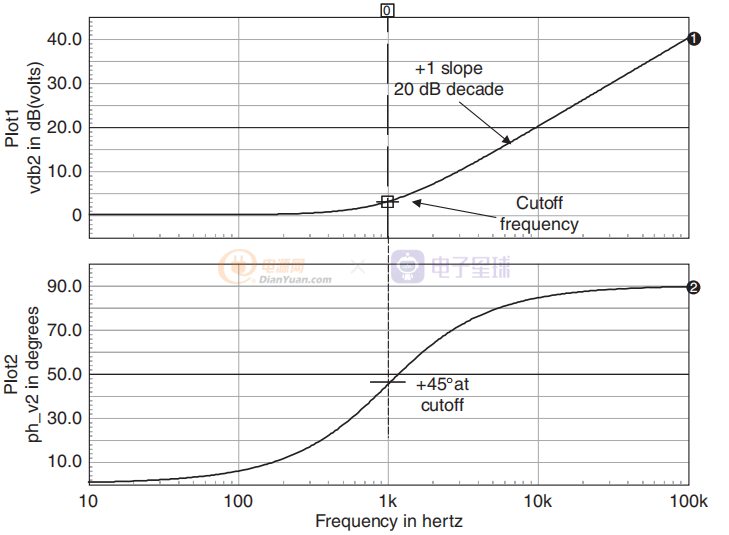
图3
回到无源电路,图 4 表示一个高通滤波器。 这种简单 RC 电路的传递函数也包含一个极点和一个零,但位于原点。 看起来像

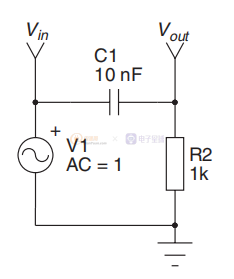
图4
该滤波器具有+20 dB/十倍频程斜率(+1 斜率)的低频渐近线和 1 或 0 dB 的高频增益。 如图 5 所示,这里我们有一个位于原点的零,使 dc (s=0) 中的传递函数为零。
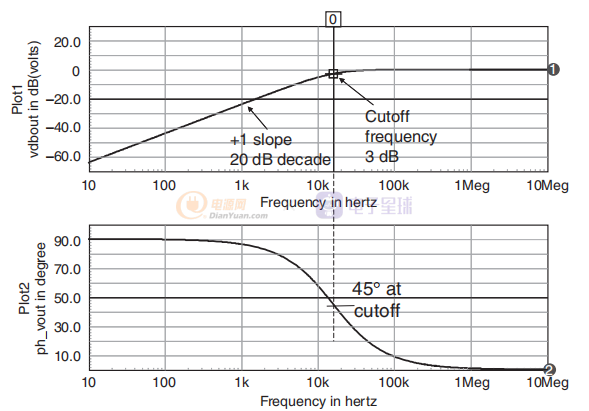
图5
在上述所有方程中,负分子根符号表示左半平面零 (LHPZ) 位置。 在一些转换器中,可能存在右半平面零 (RHPZ) 并且稳定性受到威胁。
三、右半平面零点
RHPZ 不是环路整形的一部分。 实际上碰到了 RHPZ,而不是出于稳定性目的而设计它! 它的一般形式看起来很像方程。 等式出现一个负号:

可以使用图 6 中的电路形成 RHPZ,其中我们可以看到一个有源高通滤波器,其反相输出(负号)与输入相加。 传递函数很容易推导出来
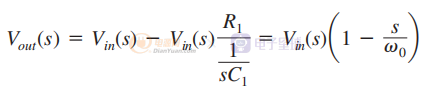
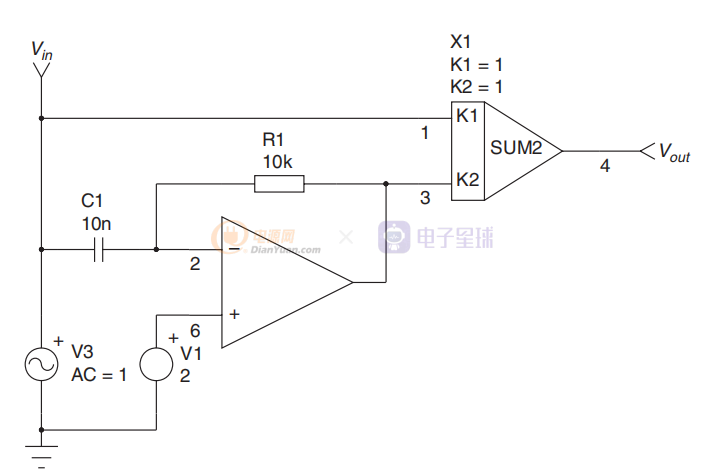
图6
如图7所示,增益输出看起来像传统的零:20 dB/十倍频程的+1 斜率,截止频率由 R1 和 C1 强加。 区别在于相位图。 “恶心心”的 RHPZ 不是相位提升,而是为您提供相位滞后,并进一步降低努力设计的相位裕度。
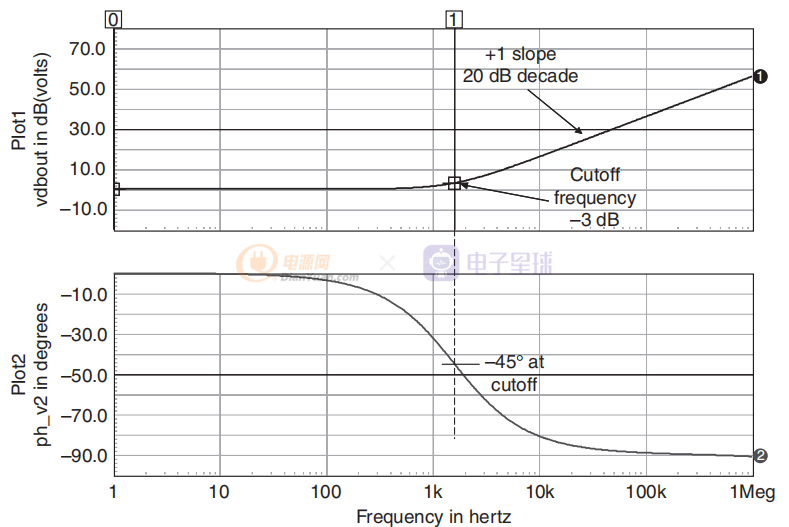
图7
右半平面零点通常存在于间接能量传输转换器中,其中能量首先存储(导通时间),然后被转储到输出电容器中(关断时间)。 如果我们以升压转换器为例,平均二极管电流等于负载直流电流。 该二极管电流 Id 实际上等于关断时间期间的电感器电流 IL 或 d Tsw。 因此它的平均值可以写成
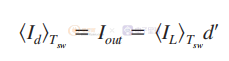
假设我们在 CCM 操作的升压转换器中有 40% 的占空比。 发生突然的负载阶跃,通过反馈回路,将占空比推至 50%。 电感中的电流相应增加,但二极管中的平均输出电流呢? 它下降是因为随着 d'=1-d,如果 d 增加,d’会缩小,输出电容器首先放电而不是增加! 变化方向错误,直到电流在电感器中积聚,使平均二极管电流达到正确值并最终提升输出电压。由于它是一个闭环系统,因此转换器变得不稳定。 工程师对此无能为力,除了严重降低带宽以避免 RHPZ 额外的相位滞后。
然而,RHPZ 频率位置随占空比而变化。 典型的经验法则建议选择的交叉频率约为最低 RHPZ 位置的三分之一。 如果尝试增加靠近 RHPZ 位置的带宽,可能会遇到相位滞后变得太大的问题。 RHPZ 出现在 CCM 操作的转换器中,例如降压-升压、升压或反激。 RHPZ 在 DCM 中消失,尽管一些学术研究表明 DCM 中存在 RHPZ,但降级到更高的频率。
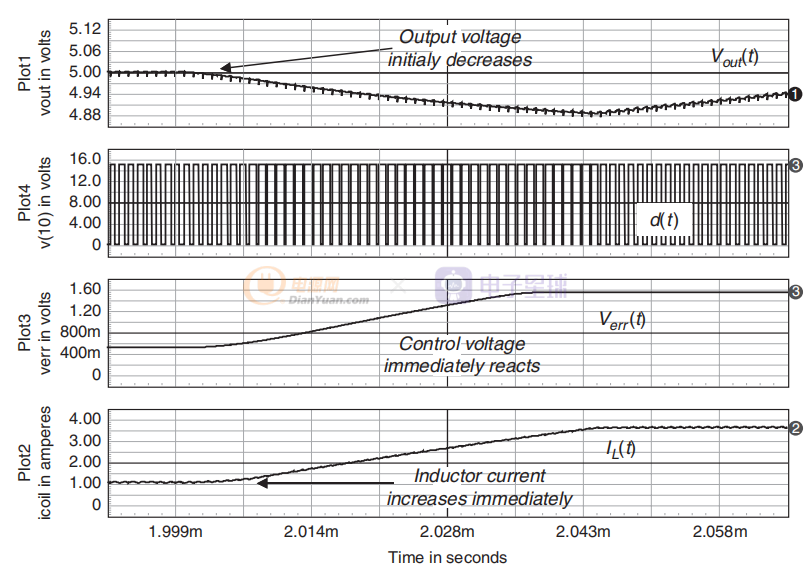
图8
图8描绘了一个具有 RHPZ 的转换器。 在存在负载阶跃时,占空比突然增加。 结果,电感电流随着开关保持闭合的时间更长而增加。 但随着 d'减小,二极管平均电流现在下降。 这种情况会导致输出电压降低,这与环路所要求的相反。 然后平均电流最终赶上电感电流,输出电压上升。
上面几个显示了无源极点和零点如何帮助塑造环路增益。然而,单独使用时,它们不提供任何直流增益,这对于低静态误差、良好的输入抑制等而言是非常需要的。 这些所谓的有源滤波器与运算放大器 (op amp) 相关联,可提供必要的传递函数以及所需的放大倍数。 确定了三种不同的类型。(下一篇会着重分析讨论)


