前言:定点是个好东西,就是编码有点难受。但是找到了一些定点编程的方法后,我们还是能理解它,掌握它,运用它。毕竟浮点的单片机很贵,定点的单片机很便宜。作者上手第一个单片机就是支持浮点的,编码的思想一直都是浮点,管你3721直接干就完了。但是最近因为需要做一些定点的功能开发,就被迫去学习一些关于定点的实现了。
定点计算的几个基本点:
-
IQ格式的定点相乘等于Q相加,除法就是减少
-
相同IQ格式的定点可以直接加减
-
可以利用移位来实现数字放大或缩小
定点的目是将浮点数字放大X倍来抵消整数计算时丢失的数字误差,比如0.0001f转为定点数字就是直接将浮点数字乘以2^X这个数字,如果IQ转换数字足够大,就可以减弱整数数值计算的误差。根据IEE754标准的单精度浮点数,小数点后的浮点数字编码最大利用到24位,因此理论上使用IQ24的定点数(#define _IQ24(A) (long) ((A) * 16777216.0L))就可以等于浮点的小数点误差。TI的IQMATH库函数默认使用IQ24的格式就是因为这个原因。
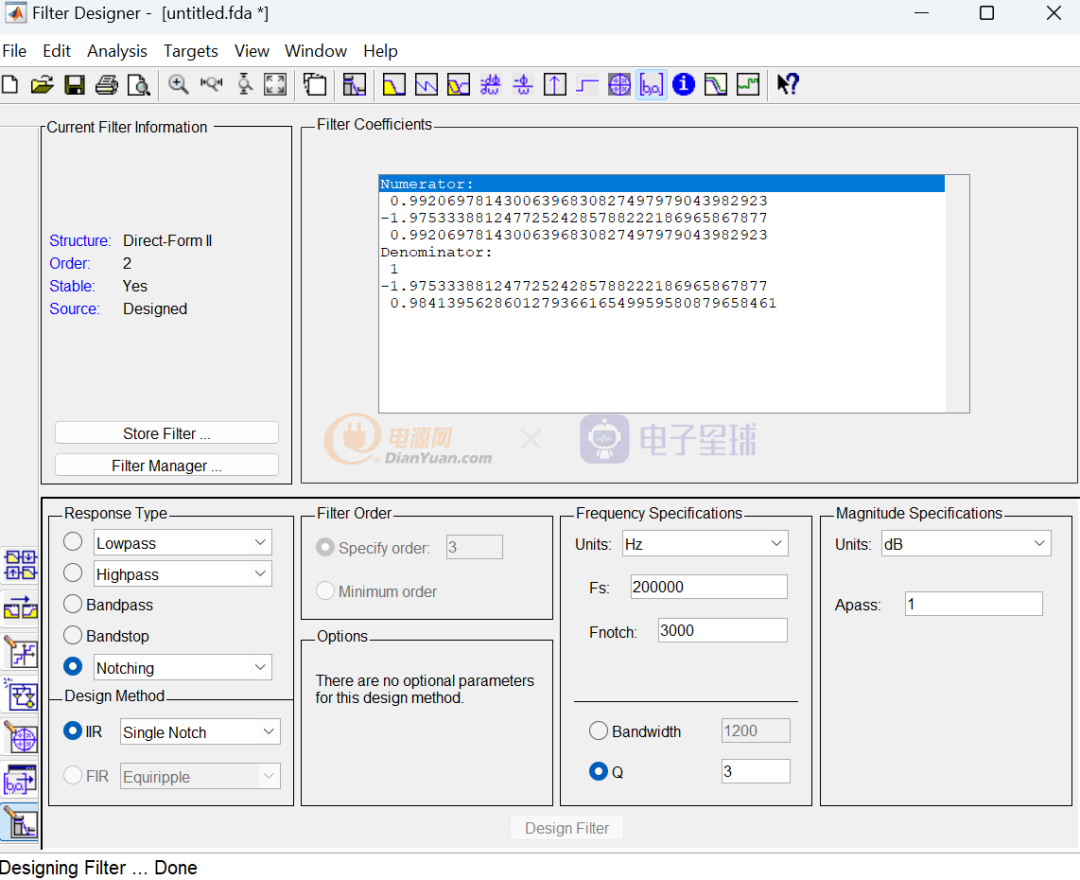
利用这一点可以使用定点计算来获得比单精度浮点更高的算法,比如高阶的滤波器设计中,时常因为采样频率非常高导致离散化之后离散传递函数中多项式中的系数很小,因为浮点数量化误差导致的滤波器误差。笔者之前就有遇到一个带通滤波器因为量化误差的问题,导致一直不能很好地运行的问题,后面是拆分成多个滤波器组合后才解决。今天了解到定点数字计算的精度还能超越浮点时,后面应付这类问题就多了一个方法。
下面尝试使用一个PI的定点实现方法来学习定点编程

实现:
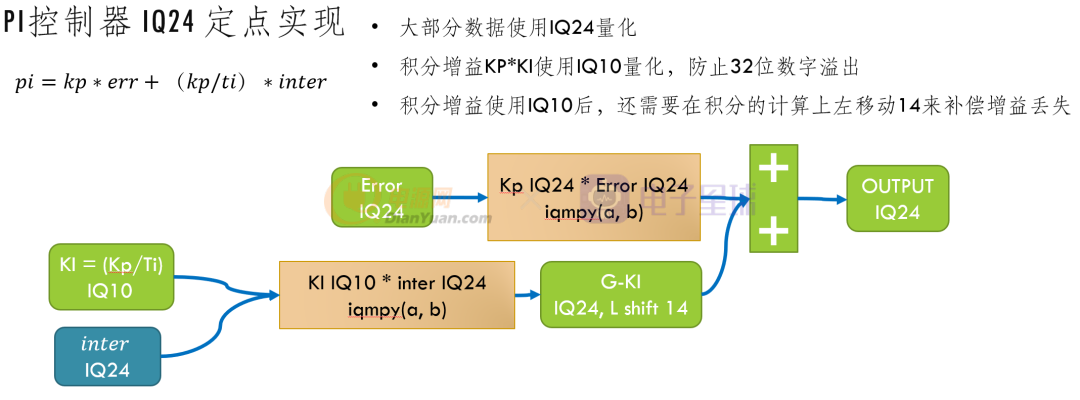
typedef struct PIF_CTRL_LAW_DATA_IQ_TAG{
Uint16 coeff_init_flag;
_iq error_1;
_iq Integrator_output_1;
_iq Integrator_output;
_iq Integrator_gain;
_iq ts;
_iq kp;
_iq ki; /* 1/ti */
_iq pi_out;
_iq output;
_iq max_out;
_iq min_out;
Uint16 integrator_sign;
// LPF
_iq lpf_a_coeff;
_iq _1_lpf_a_coeff;
_iq lpf_out_last;
_iq lpf_out;
}PIF_CTRL_IQ_DATA_DEF;
static inline _iq piF_IQ_func( _iq error,
PIF_CTRL_IQ_DATA_DEF *p,
float32 kp,
float32 ti,
float32 lpc_fc,
float32 ts,
float32 max,
float32 min)
{
if(1u == p->coeff_init_flag) //判断控制系统初始化
{
if(p->integrator_sign) //抗饱和积分,当输出饱和时停止累积误差
{
p->Integrator_output = (_IQmpy(p->ts, (error + p->error_1))) + p->Integrator_output_1;
}
else
{
p->Integrator_output = p->Integrator_output_1;
}
//更新参数
p->Integrator_output_1 = p->Integrator_output;
p->error_1 = error;
p->Integrator_gain = (_IQ10mpy(p->ki, p->Integrator_output)); //在积分增益初始时只左移了10位,这里进行IQ10*IQ24后,为了达到IQ24的精度,其实还需要左移14位,但是两个IQ24计算完成后最要右移24位,所以左移14-右移24,那就是只需要右移10即可完成计算
p->output = _IQmpy(p->kp, error) + p->Integrator_gain;
p->pi_out = p->output;
//限制幅度
if(p->pi_out > p->max_out) {p->pi_out = p->max_out;}
if(p->pi_out < p->min_out) {p->pi_out = p->min_out;}
//饱和判断
p->integrator_sign = (p->pi_out == p->output)? 1u : 0u;
// LPF
p->lpf_out = _IQmpy(p->_1_lpf_a_coeff, p->lpf_out_last) + _IQmpy(p->lpf_a_coeff, p->pi_out);
p->lpf_out_last = p->lpf_out;
}
else
{
p->error_1 = 0;
p->Integrator_output = 0;
p->Integrator_output_1 = 0;
p->Integrator_gain = 0;
p->integrator_sign = 1u;
p->output = 0;
p->pi_out = 0;
p->max_out = _IQ(max);
p->min_out = _IQ(min);
//初始化参数
p->ts = _IQ(ts * 0.5f);
p->kp = _IQ(kp);
//由于积分增益可能很大,为了在32位数字量化不溢出,仅使用IQ10来进行转换,可以接受丢失精度
p->ki = _IQ10(kp/ti); // L SHIFT 10BIT
p->lpf_out = 0;
p->lpf_out_last = 0;
//低通滤波器参数计算
float32 lpf_rc_tao = 1.0f / (lpc_fc * 2.0f * M_PI);
/* 1ORDER LPF a = Ts/(Ts + 1/(2*pi*fc)) */
float32 lpf_a_coeff_f = ts / (ts + lpf_rc_tao);
float32 _1_lpf_a_coeff_f = 1.0f - lpf_a_coeff_f;
p->lpf_a_coeff = _IQ(lpf_a_coeff_f);
p->_1_lpf_a_coeff = _IQ(_1_lpf_a_coeff_f);
p->coeff_init_flag = 1u;
}
return(p->lpf_out);
}本人能力有限,研究定点也才刚开始,如有错误恳请帮忙指正,谢谢。


