分享环路补偿TypeⅡ、TypeⅢ参数设计法

这个必须要赞一下

??

参数没有做说明，只是试着去看些

用一个极点，一个零点IP1Z 的 TYPE II 去补偿 双极点s^2的控制输出，补偿的增益中必定有s^2的关系

你的上面没有这种关系

//---------------------------------------------------------------------------------------------------------------------

说说我对环路补偿的理解吧

环路了补偿跟所有的放大器补偿是一样，目的只有一个是放大器稳定

工程计算的方法通常是以BODE图去做研究的

通过传递函数是去找出函数变化发生转折的点(叫拐点可能跟函数的里面的拐点不一样的意义，

函数的拐点是凹凸性发生改变的点)，这个转折点就是零点和极点

而不是通过去解传递函数的方程的方法

这样所有的计算就相当于做加减乘除法了，环路其实很简单的

一个极点相当于一个RC积分器

相位偏移 θ = - arctan( ω / ωp ) ,    ωp为极点频率

增益是G = -20 lg ( ω / ωp)  

同样零点相当于一个RC微分器

寻着这个思路，上面的所有计算都是很容易的

在以-1斜率的低频率段，通过提高低频段的增益，就相当于提高了相位的边界 PM

这个增益补偿完了，再反过来可以验证下就可以了，就像磁芯饱和的计算一样的。

计算不是环路的补偿的难点，难点是因为在补偿环路有很多分布参数的影响，造成相移

这个很难控制，所以才有上面提高相位的边界PM值。

其实环路补偿是很简单，真的是很简单，特别是TYPE III型补偿更简单，

增加了电路零件，而补偿变得更容易了。

先不考虑分布参数的影响，就上面附件中的例子兄台给讲讲TYPE III零、极点的设置方法？（期望的相位余量60度、10Hz处增益70dB、穿越频率20kHz，不出现条件稳定）

在BODE图上把第一个零点设置成fz1 = 0.5 * Flc , 

 第二零点 fz2 = Flc , 输出的双极点Flc

第一极点fp1 = Fesr ,  Fesr 输出的零点

第二极点fp2 = 0.5 *Fsw 

TYPE III型补偿要简单些，就像你上面说的，零点和极点相互抵消

这样变得更容易了

能讲解一下具体怎么设置？参数如何调整？如果没有单独的电容可以视为0吗？就是少一个极点。还有反激的参数是一样的计算？

按这种方法设置后的总开环bode图如下：

将穿越频率设置成预期的20kHz，10Hz处增益60.619dB，相位余量64.772度，低频增益和相位余量都没有达到预期值。（如果将相位余量设置为60度，穿越频率就不是20kHz了）

如果期望在20kHz穿越频率处的相位余量是50度，采用这种方法得到的结果依然是64.772度，这种方法跟K-factor法相似虽然设置相对简单但结果只能是固定的一种（无法得到最优参数）。

低频增益和相位余量都没有达到预期值

这个低频的增益，可以调整第一、二个零点的增益

也就是EA反馈电阻R2/R1的比值

通过补偿后，BODE图应该是闭环的增益BODE，相位BODE图

Gc(s) = Go(s)  / [  1 + Go(s) * F(s) ]

Go(s) 开环增益，Gc(s) 闭环增益, F(s) 环路补偿

调零点增益（我的理解是调原极点）可以改变低频增益同时穿越频率也会跟着改变，如果期望二者都达到预期值还需重新设置零点、极点的位置。

环路补偿中的参数一般都是改一个而关联影响好几个所以在设置上会有些麻烦，如果采用试凑法在bode图上移动零、极点也能得出差不多的结果不过需要一点经验和了解一些规律。

一楼附件中的方法就是普通解方程的方法，将所有的变量关联起来（消元）最终只剩下少量几个未知量，上述设计方法中是以极点频率fp为待设变量的。

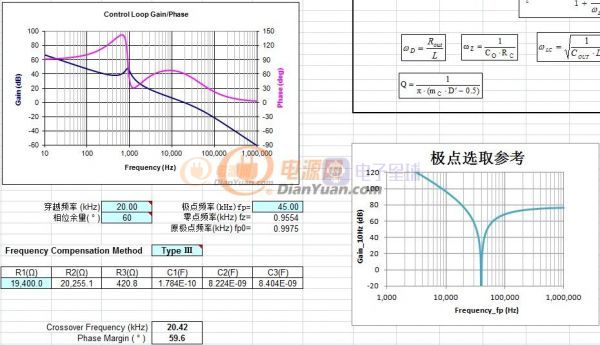
按此方法描述的曲线如上图，所有的曲线在穿越频率20kHz处的相位余量都是60度跟预期设置的值一样，这里只须选择一个合适的极点fp的值就可以了。比如上图中选极点fp=45kHz左右比较合适。

另这个补偿后的图是开环bode图既Go(s)。

环路补偿以前听过，但是不知道具体怎么回事，正好学习一下

1

这个是什么软件画的图呢x 感觉看起来好棒 比matlab的好看点

是Mathcad软件

上面说的用闭环是不正确的

一般用Go(s) * F(s)去判断闭环函数的稳定性 ，这里可以说Go(s) * F(s)是Gc(s)的特征函数

Go(s) * F(s)的模值大于1，且其在0dB时的相位Φ0与-180度差值大于45

下面的图是向量式

3Q 老夫去弄一个

谢谢分享！

顶一下

非常好的资料，感谢分享！

感谢

楼主能不能讲讲恒流源这样的环路如何补偿

补偿方法是一样的，在常规应用中采用TypeⅠ ~Type Ⅲ补偿器基本都可以胜任并且是向下兼容的。

恒流源首先要获得以电流作为反馈信号的小信号模型然后就可以采用贴中的方法进行参数配置了。

感谢你的回复。我的半桥输出，用分流器检测负载电流，10mR的电阻，电流10A时电压为100mV，利用这个作为电流反馈信号。

我用simplis仿真，得出来的开环曲线是以-40DB下降的。但是我做的实际电路中，却是以-20DB下降。怎么会差异这么大？

仿真建模时要加入寄生参数，比如电解的ESR、电感的R、导线电感等才能接近真实电路，实际电路中这些寄生参数并不容易测量所以通常是用环路扫描仪（或网分）获得的bode图。

仿真时寄生参数都有添加的。实际电路的bode图是仪器扫出来，两者相差距大。

电压环路没有问题，仿真和实际基本一致。

我把siplims文件传上来，你这边有时间帮我看看吗?

没用过这个软件，检查一下环路器件有没有饱和的或者是工作在非线性区的，比如光耦的参数配置等等，恒流、恒压静态工作点会有区别，其它好像没什么区别。

感谢大咖技术分享