直流马达EMC数学等效模型的EMC分析及对策
马达的EMC 等效数学模型如下:

从上述数学模型我们得知:直流马达的 EMC 等效模型主要由几部分组成,马达在转动过程中由于电流的不连续性会产生从低频到高频的杂散,图中等效为一个杂散电流源。L1 和 L2为马达内部连接到碳刷的两个电感,C1 和 C2 是马达金属外壳连接到 L1 和 L2 的电容,C3是马达外部直流端子之间的电容。C5 是马达内部到金属壳之间的耦合电容,C8 是金属壳到参考地之间的耦合电容,R15 是参考地回路阻抗,C3 和C7 分别是电源线正负极到参考地的耦合电容,R1 和R8 是正负电源线的等效阻抗,R16 是电源线正负极之间的等效耦合阻抗,R6 和R10 是马达金属壳分别到电容C1 和C2 的等效阻抗。 下面我们通过上述数学模型来计算流过LISN 网络中50 欧姆上的噪声电压Vs: 1)设马达中的噪声电流为Is 2)C3 和C7 的阻抗相对50 欧姆,通常情况下大很多,计算先忽略。 3)R15 相对C8 来讲也可以先忽略。 4)忽略R17 对R13 测试结果的影响。
有以下方程式:
1. Is=I1+I2
2. I2=I3+I4+I5
3. I3=I6+I7
4. I1*Z2=I2/jωC5+I4*(R10+Z5)
5. I1*Z2= I2/jωC5+ I3/jωC8+I6*(R8+50)
6. I1*Z2+(I1+I4+I6)*Z3= I2/jωC5+ I3/jωC8+I7*(R1+R16+50)
7. I2/jωC5+I5*(R6+Z4)= I1*Z2+(I1+I4+I6)*Z3
通过上述 7 个方程可以解出 I1‐I7 7 个未知量的数学表达式,在此就不再详细解过程,有兴趣可以去尝试解一下哈。
共模传导(CE)发射分析:
从上述数学模型可知,要减少CE,就必须要降低I6 和I7,要降低I6 和I7,有几个途径:
1) 降低Is,即减少马达本身的噪声电流,通过调节马达内部电感L1 和L2 以及加在外部电路板上的共模或差模电感来调节马达电流延时相位,降低马达换向时的电流突变率,或者改变碳刷的接触阻抗,但会影响马达效率。
2) 降低C5,这需要增大金属外壳和马达内部之间的空间距离,这个一般不太可行。
3) 降低C8,这个是马达本身的结构决定了的,很难改变。
4) 选择合适的C1 和C2,降低 Z4、Z5 阻抗,由于这两个电容需要跨接在外壳与内部电感之间,无法做到寄生电感值很小,改变C1 和C2 对某些频率点有改善,可能另外一些频点会恶化,需要反复测试。
5) 理论上降低 Z1 和 Z2 阻抗(在外部电感保证马达电流相位延时的情况下),有利于共模CE。但会使差模CE 和RE 恶化。
6) 直接将 C2 短路(马达负极与外壳短路),理论分析有利于电源负极的共模 CE,但测试马达负极的CE 时,对马达负极CE 起关键作用的其实还是C1 和C3。如果是马达外壳对负极理想短路的情况下,此时共模电流回流路径主要是通过 C1 和电源正极线(通过耦合阻抗R16 从负极到正极)回到骚扰源,因此,如何尽量降低C1 和C3 的等效阻抗成为重中之重。所以,即使外壳对负极短路,也不能去掉C1。
7) 在金属外壳上再包一层铜,理论上降低了R6 和R10,但也有可能引起C8 的增加,需要测试验证是否有改善。
8) 选择合适的C3,降低阻抗Z3 有利于共模和差模的CE 以及RE,但由于C3 跨接在马达的正负极之间,必然会有较大的寄生电感,这就限制了阻抗 Z3 降低的幅度,如果在外面的电路板上用无感的贴片陶瓷电容或独石电容会得到一个阻抗较低的Z3,但需要注意电容的耐压问题。 对于直圆杆导线,可以使用简单的近似计算公式:
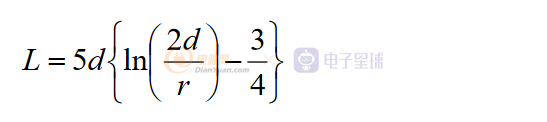
其中: L 表示导线的局部自感,单位为nH r 表示导线的半径,单位为in d 表示导线的长度,单位为in
一、电容寄生电感对CE 和RE 的影响: 下面举例说明某个频率点电容的值如何选取: 例如如果跨接在马达电源正负极之间的0.1uF 瓷片电容,引脚长20mm,直径 0.4mm,则其中一只引脚的局部电感值为:
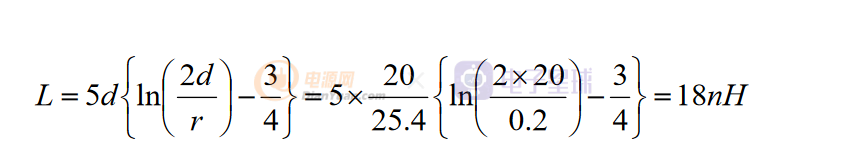
总的电感为2X18=36nH。则在70MHz 频点的阻抗大致为:
电容阻抗:

从电容的等效模型可知,如果忽略电容的Rs,则在70MHz 时,此时的电容已变为电感,阻抗为15.8j 左右,对于差模滤波来讲,效果已很差,对于共模滤波来讲,影响不如差模大。
因此,如果 C1,C2,C3 的引脚较长,譬如如果需要在 70MHZ 频点自谐振,根据引脚的长度不同,可能的电容值在 150pF—1000pF 之间(可以通过网络分析仪或阻抗分析仪测试得到),而不是0.1uF 或10nF。
二、电感寄生电容对CE 和RE 的影响:
1.5uH/10A 的磁棒电感L1 和L2,由于寄生电容的存在,其自谐振频率大概在40‐80MHz 左右,如果改为5uH/10A 的磁棒电感,会引起两个变化:
1)一方面L1 和L2 增加即增大了马达电流的相位延时,使得电流突变的幅度有所减少(有利于降低马达产生的噪声电流)。
2)另一方面由于寄生电容的增加,其自谐振频率会低于40MHz,在 70MHz 的阻抗可能反而比1.5uH 时小。 这样上述两点的变化理论上对更高频率的共模CE 都有利,但对于更高频率的差模CE 和RE影响要看马达噪声电流降低的幅度与由于L1 和L2 在更高频率阻抗降低导致差模CE 和RE 增大的幅度哪个更大,这要实际测试才能得到对比结果。
三、铸铁马达外壳的磁导率对CE 和RE 的影响:
另外,由于直流马达的外壳是铸铁制造,不同于铜的相对磁导率为μr=1 左右,其相对磁导率μr=200‐400 之间,对于高频具有磁滞损耗和涡流损耗,在高频时必然会导致 R6 和 R10增大,所以C1 和 C2 接马达外壳不同的位置会导致有不同的等效R6 和 R10 的值,当将C2去掉,直接在马达的电源负极连接到外壳,虽然从理论上将 C2 短路了,减少了由 C2 引起的阻抗,但同时可能会使R10 的值增加(等效路径可能加长了),这取决于马达不同的结构,甚至有可能R10 增加的值比C2 在对应的频率点的阻抗大,这样反而会使负极的共模CE(传导发射)在某些频点变大,所以简单的将马达外壳接电源的负极并非是解决共模CE 的唯一。
从理论上分析,在保留C1 和C2 的前提条件下,将马达外壳与电源负极短路是有利于CE 和RE 的。 通过上述分析可知,如果通过调整 C1,C2,C3 以及 L1,L2 的值,并且在马达外壳与电源负极短路的条件下,仍然无法使测试通过时,就需要在额外的电路板(该电路板需靠近马达的正负极)上增加共模滤波电感和差模滤波电容组成的滤波电路来进一步降低CE 和RE,以满足汽车电子严格的CISPR25 的等级5 标准。
对于RE 的分析,上述数学模型同样适用。


